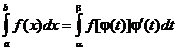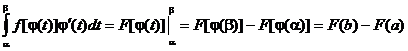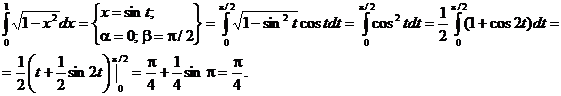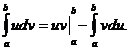Интеграл вида 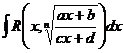 где n- натуральное число. С помощью подстановки
где n- натуральное число. С помощью подстановки 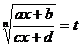 функция рационализируется.
функция рационализируется.
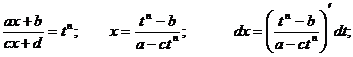
Тогда 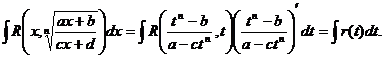
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.
Определение: Биноминальным дифференциалом называется выражение
xm(a + bxn)pdx
где m, n, и p – рациональные числа.
Метод Чебышева:
1) Если р – целое число, то интеграл рационализируется с помощью подстановки
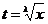 , где l - общий знаменатель m и n.
, где l - общий знаменатель m и n.
2) Если 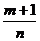 - целое число, то интеграл рационализируется подстановкой
- целое число, то интеграл рационализируется подстановкой
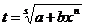 , где s – знаменатель числа р.
, где s – знаменатель числа р.
3) Если 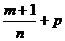 - целое число, то используется подстановка
- целое число, то используется подстановка 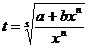 , где s – знаменатель числа р.
, где s – знаменатель числа р.
8. Определенный интеграл, его св-ва, необходимое и достаточное условие интегрируемости.
Определенный интеграл.
Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b]
Сумма 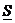 называется нижней интегральной суммой, а сумма
называется нижней интегральной суммой, а сумма 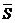 – верхней интегральной суммой.
– верхней интегральной суммой.
Т.к. mi £ Mi, то 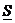 n £
n £ 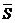 n, а m(b – a) £
n, а m(b – a) £ 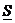 n £
n £ 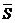 n £ M(b – a)
n £ M(b – a)
Внутри каждого отрезка выберем некоторую точку e.
x0 < e1 < x1, x1 < e < x2, …, xn-1 < e < xn.
Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].
Следовательно, 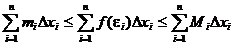
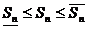
Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма 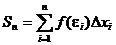 стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
Обозначение: 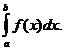
а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования.
Определение: Если для функции f(x) существует предел 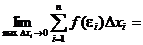
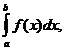 то функция называется интегрируемой на отрезке [a, b].
то функция называется интегрируемой на отрезке [a, b].
Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
Свойства определенного интеграла.
1) 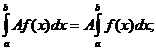
2) 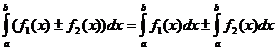 3).
3). 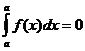
5).Если f(x) £ j(x) на отрезке [a, b] a < b, то 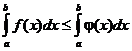
6).Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:
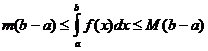
7).Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что 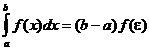
Обобщенная теорема о среднем. Если функции f(x) и j(x) непрерывны на отрезке [a, b], и функция j(х) знакопостоянна на нем, то на этом отрезке существует точка e, такая, что
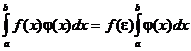
9. Интеграл с переменным верхним пределом и его свойства. Формула Ньютона – Лейбница. Формула замены переменой и интегрирования по частям для определенного интеграла.
Пусть в интеграле  нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
Обозначим 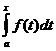 = Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.
= Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х. 
Аналогичную теорему можно доказать для случая переменного нижнего предела.
Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.
Теорема: (Теорема Ньютона – Лейбница)
Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то
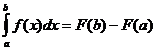
это выражение известно под названием формулы Ньютона – Лейбница.
Иногда применяют обозначение F(b) – F(a) = F(x) 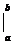 .
.
Замена переменных.
Пусть задан интеграл  , где f(x) – непрерывная функция на отрезке [a, b].
, где f(x) – непрерывная функция на отрезке [a, b].
Введем новую переменную в соответствии с формулой x = j(t).
Тогда если
1) j(a) = а, j(b) = b
2) j(t) и j¢(t) непрерывны на отрезке [a, b]
3) f(j(t)) определена на отрезке [a, b], то
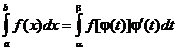
Тогда 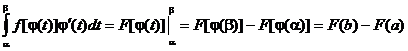
Пример.
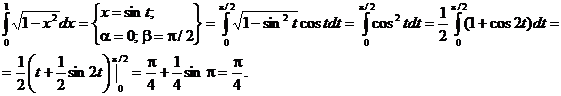
Интегрирование по частям
Если функции u = j(x) и v = y(x) непрерывны на отрезке [a, b], а также непрерывны на этом отрезке их производные, то справедлива формула интегрирования по частям:
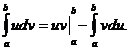
10. Геометрическое приложение определенного интеграла: вычисление площади фигуры, длины дуги кривой,объема с помощью определенного интеграла



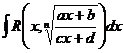 где n- натуральное число. С помощью подстановки
где n- натуральное число. С помощью подстановки 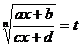 функция рационализируется.
функция рационализируется.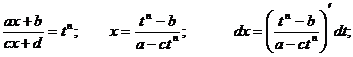
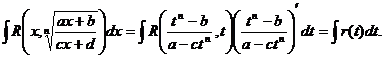
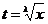 , где l - общий знаменатель m и n.
, где l - общий знаменатель m и n.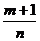 - целое число, то интеграл рационализируется подстановкой
- целое число, то интеграл рационализируется подстановкой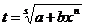 , где s – знаменатель числа р.
, где s – знаменатель числа р.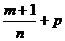 - целое число, то используется подстановка
- целое число, то используется подстановка 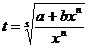 , где s – знаменатель числа р.
, где s – знаменатель числа р.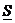 называется нижней интегральной суммой, а сумма
называется нижней интегральной суммой, а сумма 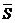 – верхней интегральной суммой.
– верхней интегральной суммой.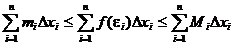
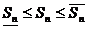
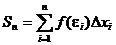 стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].
стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b].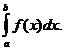
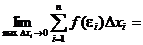
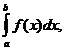 то функция называется интегрируемой на отрезке [a, b].
то функция называется интегрируемой на отрезке [a, b].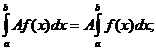
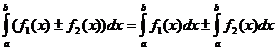 3).
3). 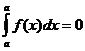
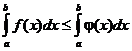
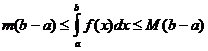
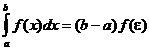
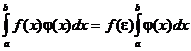
 нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.
нижний предел а = const, а верхний предел b изменяется. Очевидно, что если изменяется верхний предел, то изменяется и значение интеграла.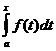 = Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х.
= Ф(х). Найдем производную функции Ф(х) по переменному верхнему пределу х. 
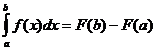
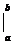 .
.