Примеры:
Чтобы получить список размещений без повторений, необходимо выполнить:
> permute([1,2,3],3);
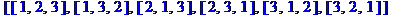
Чтобы получить список размещений c повторениями из n элементов по m,необходимо в списке n каждый элемент повторить m раз:
> permute([1,1,1,2,2,2,3,3,3],3);
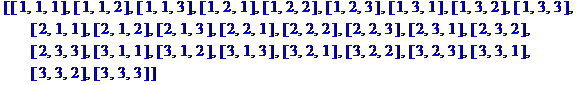
или тоже самое:
> permute([1$3,2$3,3$3],3);
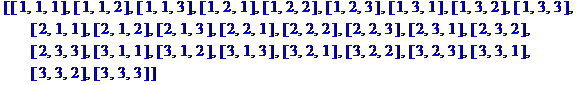
или тоже самое:
> permute(['$1..3'$3],3);

> numbperm([1,2,3],3);

> numbperm([1,1,1,2,2,2,3,3,3],3);

или тоже самое:
> numbperm([1$3,2$3,3$3],3);

или тоже самое:
> numbperm(['$1..3'$3],3);

Вычисление факториала:
Оператор:! -вычисляет факториал.
Пример:
> 5!;
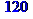
> 5!!;

Рассмотрим теперь решение конкретных задач.
Задача 1. Сколько разных 5-разрядных чисел можно составить из 10 цифр? Для упрощения задачи будем считать, что в первый разряд тоже можно поместить цифры от 0 до 9.
Решение: так как порядок цифр имеет значение и цифры могут повторяться, то это размещение с повторениями из 10 по 5.Поэтому:
> with(combinat):
> numbperm(['$1..10'$10],5);

Задача 2. Сколькими способами можно выбрать три различные
краски из имеющихся пяти?
Решение: Так как не имеет значение порядок выбора красок и краски различны, то это сочетание без повторений из 5 по 3. Поэтому:
> numbcomb(5,3);
или применяя другую функцию:
> binomial(5,3);
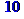
Задача3.
Предстоит выбрать команду четырех игроков в гольф из 5 профессиональных игроков и пяти любителей. Сколько разных команд может состоять из 3 профессионалов и 1 любителя?
Так как порядок выбора игроков не важен и нет повторений, то это задача на сочетание без повторений. Трех профессионалов мы можем выбрать  способами, кним
способами, кним  способами мы можем выбрать любителя. По правилу произведения имеем
способами мы можем выбрать любителя. По правилу произведения имеем  способов.
способов.
Задание:
1. Решить комбинаторные задачи 1, 2, 3, 5 согласно вашему варианту с использованием программы Maple.
2. Составить программу на С решения задачи 4 согласно варианту. Вычисление факториала оформить в виде функции. Пример использования функции в программе приведен в конце лабораторной работы.
Варианты заданий.
| №
вар.
| №
| Задача
|
| 1.
| 1.
| Вычислить максимальное количество чисел, которые можно представить в двоичной системе восьмиразрядным числом.
|
| 2.
| Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал пяти различных цветов?
|
| 3.
| Сколькими способами можно составить набор из 8 пирожных, если имеется 4 сорта пирожных?
|
| 4.
| Сколько существует перестановок элементов 1, 2,..., n, в которых элемент 1 находится не на своём месте?
|
| 5.
| При опросе 13 человек, каждый из которыхзнает, по крайней мере, один иностранный язык, выяснилось, что10 человек знают английский язык, 7- немецкий, 6 - испанский,5 - английский и немецкий, 4 - английский и испанский, 3 - немецкий и испанский. Сколько человек знают: а) всетри языка? б) ровно два языка? в) только английский?
|
|
| 1.
| Вычислить максимальное количество чисел, которые можно представить в шестнадцатеричной системе четырехразрядным числом.
|
| 2.
| Сколько четырехзначных чисел, не превосходящих 6000, можно составить, используя только нечетные числа?
|
| 3.
| Сколькими способами можно переставить буквы в слове «математика»
|
| 4.
| Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал пяти различных цветов и среди полос одна обязательно должна быть красной.
|
| 5.
| В НИИ работают 67 человек. Из них 47 человек знает английский язык, 35 – немецкий, 20 – французский, 12 человек знает английский и французский, 11 человек – немецкий и французский, 23 – английский и французский, 5 человек знает все три языка. Сколько человек в институте не знает ни одного языка?
|
| 3.
| 1.
| Пароль состоит из 3-х латинских букв и 5 цифр. Сколько паролей можно составить из этого набора?
|
| 2.
| Пассажир оставил вещи в автоматической камере хранения, а когда пришел получать вещи, выяснилось, что он забыл номер. Он только помнит, что в номере были числа 23 и 37. Чтобы открыть камеру нужно правильно набрать пятизначный номер. Какое наибольшее количество номеров нужно перебрать, чтобы открыть камеру?
|
| 3.
| Сколько имеется пятизначных чисел, которые делятся на 5?
|
| 4.
| Сколькими способами можно распределить 15 студентов по 3-м учебным группам по 5 студентов в каждой?
|
| 5.
| Сколькими способами можно переставить буквы в слове «математика»?
|
| 4.
| 1.
| Четверо студентов сдают экзамен. Сколькими способами могут быть поставлены им оценки (по пятибалльной системе), если известно, что никто не получил оценки “неудовлетворительно”?
|
| 2.
| Хоккейная команда насчитывает 18 игроков, 11 из них входит в основной состав. Подсчитайте количество возможных составов.
|
| 3.
| Перевертыш – это многозначное число, которое не поменяет своего значения, если все его цифры записать в обратном порядке. Сколько существует шестизначных перевертышей? Сколько существует семизначных?
|
| 4.
| При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?
|
| 5.
| Сколько различных «слов» можно получить из слова «абракадабра»? Сколько из них начинается на букву «к»?
|
| 5.
| 1.
| Сколько существует двузначных чисел, у которых обе цифры четные?
|
| 2.
| Сколько четырехбуквенных слов можно образовать из букв слова «интеграл»?
|
| 3.
| В роте имеется три офицера и сорок солдат. Сколькими способами может быть выделен наряд, состоящий из одного офицера и трех солдат?
|
| 4.
| Сколькими способами можно разместить 12 человек по трем комнатам, если в первую можно поместить два, во вторую шесть, а в третью четыре человека?
|
| 5.
| Сколькими способами можно расставить на шахматной доске 8 ладей так, чтобы они не могли бить друг друга?
|
| 6.
| 1.
| Сколько имеется пятизначных чисел, которые делятся на 5?
|
| 2.
| Сколько существует возможностей для присуждения первого, второго и третьего мест 14 участницам соревнований по гимнастике?
|
| 3.
| В концерте участвуют три певца и две певицы, каждый участник с одним номером. Сколькими способами можно составить программу, если концерт должен начинаться и заканчиваться выступлением певца?
|
| 4.
| Из колоды, содержащей 52 карты, вынули 10 карт. В скольких случаях среди этих карт окажется ровно один туз?
|
| 5.
| На диск сейфа нанесены 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова?
|
Пример (ОА и П):
15.Написать пpогpамму,котоpая выводит квадраты натуральных чисел
в виде таблицы 2 2 2 2 2
1 2 3 4 5
2 2 2 2 2
6 7 8 9 10
..........
2 2 2 2 2
96 97 98 99 100;
#pragma argsused
#include <conio.h>
#include <stdio.h>
int f(int n) //îïðåäåëåíèå ôóíêöèè f
{
n=n*n;
return n;
}
int main(int argc, char* argv[]) //îïðåäåëåíèå ôóíêöèè main
{
int m,i;
for(m=1;m<=20;m++)
{
for(i=m*5-4;i<=m*5;i++)printf(" %6.d ",f(i)); //â ôóíêöèè printf
printf("\n"); //âûçûâàåòñÿ ôóíêöèÿ f
};
getch();
return 0;
}





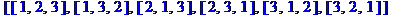
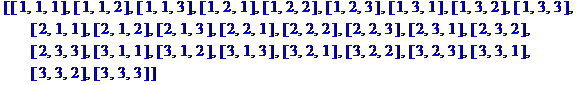



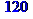


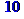
 способами, кним
способами, кним  способами мы можем выбрать любителя. По правилу произведения имеем
способами мы можем выбрать любителя. По правилу произведения имеем  способов.
способов.


