Пусть L – спрямляемая кривая комплексной плоскости с началом в точке А и концом в точке В. Если существует интегральной суммы  (где
(где  ) при max|
) при max|  |->0, то он называется интегралом функции комплексной переменной f(z) по кривой L и обозначается
|->0, то он называется интегралом функции комплексной переменной f(z) по кривой L и обозначается 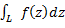 .
.
Пусть теперь L –гладкая кривая, заданная комплексным параметрическим уравнением z=z(t)=x(t)+iy(t), где t1 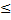 t
t 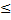 t2, а f(z)=u(x,y)+iv(x,y) – непрерывная и однозначная функция, определенная на L. Тогда
t2, а f(z)=u(x,y)+iv(x,y) – непрерывная и однозначная функция, определенная на L. Тогда  ,
,  . Следовательно
. Следовательно

Переходя к max|  получаем:
получаем:

Или 
Основные свойства интеграла:
1) Если кривую L ориентировать в обратную сторону (от В до А) то интеграл поменяет знак
2) Сумма подынтегральных функций равна сумме интегралов этих функций
3) Комплексное число помноженное на подынтегральную функцию можно вынести за знак интеграла
4) Если кривая L представлена в виде суммы двух кривых L1 и L2, то интеграл по кривой L будет равен сумме интегралов по L1 и L2
5) Если во всех точках кривой L справедливо неравенство |f(z)<M, то модуль интеграла будет меньше M*l, где l – длина кривой L.
Формула Ньютона-Лейбница
Интеграл от аналитической на односвязной области D функции не зависит от пути интегрирования, а зависит лишь от начальной и конечной точек этого пути.

Восстановление аналитической функции по ее вещественной (мнимой) части.
Если действительная (мнимая) часть аналитической функции является гармонической, то есть удовлетворяет уравнению Лапласа

Тогда из условия Коши-Римана можно попробовать восстановить не хватающую часть, путем дифференцирования имеющейся части по одной переменной, и последующим интегрированием по другой переменной.
Интегральная теорема Коши (в т.ч. для многосвязной области; правило обхода границы).
Теорема: если функция комплексной переменной f(z), аналитическая в односвязной области D, то интеграл от f(z) по любому кусочно-гладкому замкнутому контуру L, лежащему в области D, равен нулю.  .
.
Теорема: Пусть функция f(z) аналитическая на односвязной области D. Тогда интегралы от аналитической функции f(z) вдоль двух любых кривых, имеющих общее начало и конец, имеют равные значения.
Теорема для многосвязной области: пусть область D ограничена ориентированным кусочно-гладким контуром L. Тогда для функции f(z)аналитической на замкнутой области 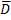 , справедливо равенство
, справедливо равенство  . Из этой теоремы получается следующая:
. Из этой теоремы получается следующая:
Теорема: пусть область D ограничена внешним контуром L и внутренними контурами L1,L2,…,Ln, которые ориентированы против часовой стрелки. Тогда для функции f(z), аналитической на замкнутой области 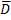 , справедливо утверждение, что интеграл функции по контуру L равен сумме интегралов внутренних контуров.
, справедливо утверждение, что интеграл функции по контуру L равен сумме интегралов внутренних контуров.
Если при обходе границы контура область D остается слева, то такой контур называют положительно ориентированным. И наоборот.



 (где
(где  ) при max|
) при max|  |->0, то он называется интегралом функции комплексной переменной f(z) по кривой L и обозначается
|->0, то он называется интегралом функции комплексной переменной f(z) по кривой L и обозначается 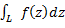 .
.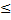 t
t  ,
,  . Следовательно
. Следовательно
 получаем:
получаем:



 .
.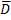 , справедливо равенство
, справедливо равенство 


