· В языке Математики малые и большие буквы различаются.
· Названия всех встроенных функций и констант начинаются с большой буквы; поэтому, во избежание недоразумений, рекомендуется вводимые пользователем идентификаторы начинать с малой буквы.
· Аргументы функций пишутся в квадратных скобках.
· Знак умножения (*) можно опускать, заменяя его в случае необходимости пробелом. Несколько примеров представления оператора умножения:
2a эквивалентно 2*a,
a b эквивалентно a*b,
a(x+y) эквивалентно a*(x+y),
Sin[x]2 эквивалентно 2 Sin[x], эквивалентно 2*Sin[x].
Однако, выражения " a2 ", " ab " воспринимаются Математикой как единые идентификаторы. Выражение " aSin[x] " воспринимается как идентификатор новой функции.
· Круглые скобки используются для объединения объектов или операндов, как это принято обычно в математических выражениях. При этом соблюдаются обычные соглашения о приоритетах математических операций, поэтому в ряде случаев скобки можно опускать. Например, Sin[x]^2/2 есть сокращенная запись более полного выражения ((Sin[x])^2)/2.
· Значения строковых переменных записываются в кавычках.
· Комментарии внутри активной ячейки выделяются знаками (* и *). Пример:
In[ ]: = (* Определим константу: *) a=Log[10, 2.] Out[ ] =0.30103
· Фигурные скобки используются при описании списков, в частности, массивов, и для задания пределов изменения переменной величины. Пример списка приведен во второй строке таблицы 5.1.
· Как правило, допустимы пробелы в выражениях. Например, Sin [Pi / 2] воспринимается как Sin[p/2]. Однако, пробелы в служебных словах – недопустимы. Пробелы в словах воспринимаются как знак умножения. Например, P i воспринимается уже не как число p, а как результат перемножения символов P и i.
·  Точка с запятой в конце выражения служит знаком запрета вывода результата на экран.
Точка с запятой в конце выражения служит знаком запрета вывода результата на экран.
· Косая черта " \ " в конце строки означает, что выражение продолжается в следующей строке. Этот знак можно опустить, если в строке помещено явно незаконченное выражение: отсутствует закрывающая скобка, отсутствует необходимый операнд и т.п. Отметим, что, если в конце строки стоит знак " \ ", то пустые позиции в начале следующей строки игнорируются.
Примеры выражений даны в таблице 5.1.
Основные константы:
E или <Esc>ee<Esc> – основание натуральных логарифмов; I – мнимая единица;
Infinity или <Esc>inf<Esc> – бесконечность; Pi или <Esc>p<Esc> – число "пи".
Символы указанных констант также могут быть взяты из палитры Basic Input.
Приведем некоторые наиболее часто используемые функции.
Floor[x], Ceiling[x] – целыечисла, ближайшие к действительному числу x (меньшее и большее).
Round[x, eps] – округление числа x до ближайшего числа с точностью eps.
Пример 5.1 In[]:= Round[20/3, 4] Out[]= 8,
In[]:= Round[20/3, 3] Out[]= 6,
In[]:= Round[20/3, 0.02] Out[]= 6.66,
In[]:= Round[20/3, 0.01] Out[]= 6.67.
x^y – x в степени y.
Exp[x] или E^x – экспоненциальная функция аргумента x;
Sin[x], Cos[x], Tan[x], Cot[x], ArcSin[x], ArcCos[x] и т.д. - прямые и обратные тригонометрические функции.
Log[z] – натуральный логарифм числа z.
Log[b, z] – логарифм числа z по основанию b.
Sqrt[a] – квадратный корень числа a.
Вычисление пределов:
Limit[ expr, x –> x0] – предельное значение выражения expr при x стремящемся к x0. Более полный формат команды: Limit[ expr, x –> x0, Direction –> 1] – нахождение предела при x стремящемся к x0 слева. Соответственно, Direction –> -1 – нахождение предела справа.
Пример 5.2 In[]:= f[t_]=Sin[t]/t; Limit[f[t], t->0] Out[]= 1,
In[]:= Limit[ Tan[fi], fi –> Pi / 2, Direction –> -1] Out[]= -Infinity.
Замечание. Функция вычисления пределов не вызывается автоматически. Если, например, в ходе вычислений встречается выражение вида 0/0, то вычисления прекращаются. Например, Математика отказывается вычислять f[0] в примере 5.2.
Правило преобразования Rule:
lhs –> rhs – левая часть выражения заменяется на правую.
Функция замещения ReplaceAll[expr, rule] – применяет правило преобразования rule (lhs –> rhs) к выражению expr – каждое вхождение lhs заменяется на rhs. Та же функция может быть записана более коротко с помощью оператора замещения “ /. ” (произносится “slash-dot”):
expr /. lhs –> rhs
Может быть задана последовательность правил преобразования:
expr /. {lhs1 –> rhs1, lhs2 –> rhs2,…}
Может также быть задан список списков правил: expr /. {{lhs –> rhs1}, {lhs –> rhs2},…}, –
в этом случае на выходе мы получим список результатов.
Пример 5.3
Простая замена: In[]:= 1 + x + x^2 /. x –> Sin[x] Out[]= 1 + Sin[x] + Sin[x]2.
Применение списка правил замены:
In[]:= {a, b, c} /. {a –> b, b –> d} Out[]= {b, d, c}.
Последовательное применение тех же правил замены дает другой результат:
In[]:= {a, b, c} /. a –> b /. b –> d Out[]= {d, d, c}.
Применение списка списков правил замены
In[]:= x + y /. {{x –> 2}, {y –> 5}}
дает список результатов: Out[]= {2 + y, 5 + x}.
Дифференцирование:
D[f, x] – производная функции f по аргументу x.
D[f, {x, n}] – производная порядка n.
D[f, x1, x2, …] – смешанная производная функции f по аргументам x1, x2, и т.д.
Другое обращение к производной:
f’[x], f’’[x], f’’’[x] – соответственно, первая, вторая и третья производная функции f[x].
Для обращения к производной можно воспользоваться также “заготовкой”, имеющейся в палитре Basic Math Input.
Пример 5.4 In[]:= D[Sin[x], x] Out[]=Cos [x],
I n[]:= D[Sin[x], x] /. x –> 0 Out[]= 1,
In[]:= Sin'[x] Out[]= Cos[x],
In[]:= Sin'[0] Out[]= 1.
Дифференцирование сложных функций:
In[]:= D[f[g[x]], x] Out[]= 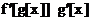 ,
,
In[]:= D[f[x, y[x]], x] Out[]= 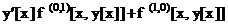 ,
,
In[]:= D[Sin[x^2], x] Out[]=2 x Cos[x2],
In[]:= D[x Log[x], x] Out[]=1 + Log[x].
Вычисление смешанной производной:
 In[]:= D[x^3 / y, {x, 2}, y] Out[]= - 6x / y2.
In[]:= D[x^3 / y, {x, 2}, y] Out[]= - 6x / y2.
Интегрирование:
Integrate[f, x] – неопределенныйинтеграл.
Integrate[f, {x, xmin, xmax}] – определенный интеграл на отрезке от xmin до xmax.
Integrate[f, {x, xmin, xmax}, {y, ymin, ymax}] – кратный интеграл.
NIntegrate – численное интегрирование.
“Заготовка” для интеграла имеется в палитре Basic Math Input.
Пример 5.5
In[ ]: = Integrate[ Exp[-x], {x, 0, Infinity}] Out[ ] = 1,
In[ ]: = NIntegrate[ 2 / Sqrt[2 Pi] Exp[-x^2 / 2], {x, 0, 3}] Out[ ] = 0.9973,
In[ ]: = Integrate[ 3 u Sin[v]^2 Cos[v]^2, {u, 0, a}, {v, 0, 2Pi}] Out[ ] = 3 a2 Pi / 8.
Нахождение экстремумов:
Функции FindMinimum[f, {x, x0}], FindMaximum[f, {x, x0}] позволяют найти локальный минимум или максимум функции f, ближайший к точке x0.
Функции возвращают список: {fmin, {x –> xmin}] – где xmin – точка экстремума, fmin – значение функции f в точке экстремума.
Пример 5.6
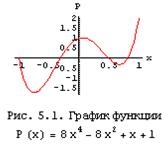
Нахождение экстремумов функции P[x_]=8x^4-8x^2+x+1 (рис. 5.1).
In[ ]: = FindMinimum[ P[x], {x, 2}] Out[ ] = {-0.309, {x –> 0.673}},
In[ ]: = FindMinimum[ P[x], {x, -2}] Out[ ] = {-1.722, {x –> -0.736}}.
In[ ]: = FindMaximum[ P[x], {x, 0}] Out[ ] = { 1.031, {x –> 0.063}}.
Функции FindMinimum[f, {x, x0}, {y, y0},…], FindMaximum[f, {x, x0}, {y, y0},…] позволяют найти локальные экстремумы функции нескольких аргументов.
Пример 5.7
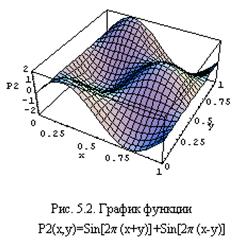
Нахождение локальных экстремумов функции двух переменных:
P2[x_,y_]=Sin[2Pi(x+y)]+Sin[2Pi(x-y)], (Рис. 5.2).
In[ ]: = FindMaximum[P2[x, y], {x, 0.5}, {y, 0.5}] Out[ ] = {2., {x®0.75,y®0.5}}
In[ ]: = FindMinimum[P2[x, y], {x, 0.5}, {y, 0.5}] Out[ ] = {-2., {x®0.25,y®0.5}}
 Генераторы случайных чисел:
Генераторы случайных чисел:
RandomReal[range] – дает псевдослучайное число типа Real с равномерным распределением в диапазоне range.
RandomInteger[range] – дает псевдослучайное число типа Integer со значениями в диапазоне range.
RandomComplex[range] – дает псевдослучайное число типа Complex со значениями в диапазоне range.
Для всех типов псевдослучайных чисел диапазон range задается списком, включающим минимальную и максимальную границы: {imin, imax}. Если диапазон не указан, то по умолчанию он равен {0, 1}.
Для комплексных псевдослучайных чисел диапазон range задается минимальным и максимальным комплексным числом. По умолчанию он равен {0+0 I, 1+1 I}.
Простейшие циклические операции:
Sum[f, {i, imin, imax, di}] – суммирование значений функции f по индексу i в пределах от imin до imax с шагом di;
Sum[f, {i, imin, imax}, {j, jmin, jmax}] – вычисление двойной суммы;
Product[f, {i, imin, imax}] – вычисление произведения.
В циклических операциях значения di и imin можно опускать, если эти значения равны единице; в тех случаях, когда значения функции f не зависят от индекса, индекс можно не указывать.
Пример 5.8
In[ ]: = Sum[x^i/i!, {i, 0, 3}] Out[ ] = 1 + x + x2/2+x3/6
In[ ]: = Product[x-i, {i, 0, 3}] Out[ ] = (-3+x) (-2+x) (-1+x) x
In[ ]:= Product[ x - Random[Integer, {-9, 9}], {3}] Out[ ] = (-7+x) (-2+x) (8+x) – один из возможных ответов.
Обратим внимание, что Математика соблюдает определенный порядок при выводе результатов; в частности, сомножители сортируются в порядке возрастания их значений.
Циклические операции могут быть описаны также с помощью математических символов, имеющихся в палитре Basic Math Input.
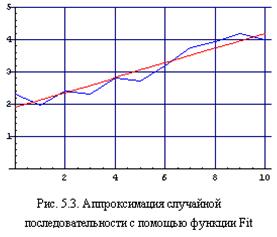
Функция Fit[data, funs, vars]. Эта функция находит такую линейную комбинацию функций, заданных в списке funs, которая аппроксимирует данные data с наименьшей среднеквадратичной ошибкой. Vars – список аргументов функций funs. Данные data могут быть заданы в виде списка {{x1, y1,…,f1}, {x2, y2,…,f2},…}, где количество координат x,y,… должно быть равно количеству аргументов функций funs.
Пример 5.9 Требуется аппроксимировать последовательность точек: data=
{{0, 2.3}, {1, 2.0}, {2, 2.4}, {3, 2.3}, {4, 2.8}, {5, 2.7}, {6, 3.2}, {7, 3.8}, {8, 3.9}, {9, 4.2}, {10, 4}}, –
 линейной зависимостью. Решение:
линейной зависимостью. Решение:
In[]: = Fit[ data, {1., x}, x]
Out[] = 1.90909 +0.229091 x
Аппроксимируемая последовательность точек (для наглядности соединенных ломаной синей линией) и аппроксимирующая прямая линия (красного цвета) показаны на рис. 5.3.
Функция Print[ expr1, expr2,… ] – печатает выражения expri, соединяя их.
Пример 5.10
In[ ]: = Print["Объем куба со стороной ",
v=4," равен ", v^3]
Out[] = Объем куба со стороной 4 равен 64
Обращение к функциям в системе Математика может быть записано в разных формах:
f[x] - стандартная форма (standard form),
 f@x - префиксная форма (prefix form),
f@x - префиксная форма (prefix form),
x//f - постфиксная форма (postfix form).
Примеры обращений даны в таблице 5.2.
Отметим, что префиксная форма имеет наиболее высокий приоритет, а постфиксная – самый низкий, так что Sin@x+y = y+Sin[x], а x+y//Sin = Sin[x+y].
Для функций нескольких переменных кроме стандартной существует также инфиксная форма. Обычная запись суммы (x+y) и произведения (x*y) является инфиксной формой. Примеры функций двух аргументов даны в таблице 5.3.
Функции, вводимые пользователем, также могут быть записаны в разных формах.
Получить информацию о любой функции можно с помощью команды: ?заголовок функции.
Напомним полезную команду меню Edit – Complete Selection (Ctrl+K), позволяющую автоматически закончить начатое слово. Достаточно написать начало слова и нажать клавиши Ctrl+K – появится список слов, из которого можно выбрать нужное слово, просто щелкнув на нем мышкой.
 6. Функции комплексного аргумента
6. Функции комплексного аргумента
Перечисленные в предыдущем разделе функции применимы также и к комплексному аргументу. Дополнительные функции комплексного аргумента:
Re[z], Im[z] - действительная и мнимая части числа z,
Arg[z] - аргумент числа z.
Пример 6.1
In[ ]: = Abs[1+I] Out[] = 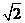
In[ ]: = Cos[I] Out[] = 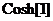
In[ ]: = Sqrt[2I] Out[] = 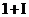 In[ ]: = Log[I] Out[] =
In[ ]: = Log[I] Out[] = 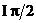
In[ ]: = E^(I p) Out[] = -1 In[ ]: = Arg[1+I] Out[] = 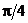
Замечание 1. В ряде случаев Математика по умолчанию не упрощает выходные выражения. Например, входное выражение 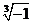 Математика просто переписывает в ином виде. Для упрощения выражений можно применить функцию ComplexExpand[expr] – вычисление всех степеней и произведений в выражении expr – либо где-нибудь в выражении expr поставить десятичную точку.
Математика просто переписывает в ином виде. Для упрощения выражений можно применить функцию ComplexExpand[expr] – вычисление всех степеней и произведений в выражении expr – либо где-нибудь в выражении expr поставить десятичную точку.
Пример 6.2. На языке пакета Математика напишем список из трех выражений для извлечения
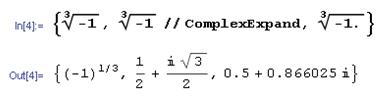
корня третьей степени:
Получим следующий ответ:
.
Замечание 2. При извлечении корня из комплексного числа Математика по умолчанию выдает значение корня с наименьшим (по абсолютной величине) значением аргумента.
Пример 6.3.
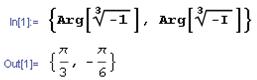 Найдем аргумент кубичного корня из –1 и –I. Запишем на языке пакета Математика:
Найдем аргумент кубичного корня из –1 и –I. Запишем на языке пакета Математика:
Получим ответ:
Чтобы найти все n значений корня степени n можно воспользоваться функциями для решения уравнений Solve, FindRoot или Roots.
Пример 6.4. Найдем все значения корня третьей степени из –1 и –I:
In[]: = Roots[x^3 == -1,x] //ComplexExpand,
Out [] = 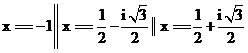 .
.
In[]: = Roots[x^3 == -I,x] //ComplexExpand,
Out [] = 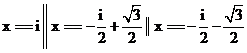 .
.
Циклические операции
7.1. Цикл For.
 Формат команды: For[start, test, incr, body]
Формат команды: For[start, test, incr, body]
Функция For имеет не более четырех аргументов. Аргумент start описывает предварительные действия. Test – проверка условия выполнения цикла. Необязательный аргумент incr – увеличение индекса – счетчика циклов. Body – тело цикла. Сначала выполняется start, затем повторно выполняются body и incr до тех пор, пока значение test есть ИСТИНА (True). Аргументы оператора For отделяются друг от друга запятыми, формулы внутри аргументов отделяются друг от друга знаком точка с запятой.
Пример 7.1
Программа, иллюстрирующая работу цикла For. Программа включает два оператора: цикл For, в котором подсчитывается значение целой величины I, и команду вывода на экран найденного значения.
In[]: = For[ i=1, i<5, i++]; i
Out [ ] = 5
Обратим внимание на момент окончания цикла. При i=4 условие i<5 выполнено, так что величина i еще раз увеличивается на единицу, и окончательное значение равно 5.
Пример 7.2
Составим программу вычисления “машинного эпсилон” – числа, которое определяет относительную точность арифметики, использующей представление чисел с плавающей запятой. По определению машинный эпсилон eps – это минимальное положительное число, для которого выполняется условие: 1. + eps > 1. Иначе говоря, это минимальное число, при котором правая и левая части в этом неравенстве различимы. Программа имеет вид:
In[]: = For[ep=1., 1.+ep>1., ep=ep/2]; 2 ep
Out [ ] = 2.84217*10-14
Сначала числуepприсваивается значение 1.0, затем это число многократно делится пополам до тех пор, пока не нарушится условие выполнения цикла. На печать выводится значение ep, полученное на предпоследнем шаге.
7.2. Цикл While.
Формат команды: While[test, body] – подсчитываются повторно условие test и тело цикла body до тех пор, пока истинность условия не нарушится.
7.3. Цикл Do.
Формат команды: Do[body, {i, imin, imax, di}] – подсчитывается выражение expr для значений i, принимающих значения от imin до imax с шагом di. Значения imin и di можно не указывать, если эти значения равны 1. Индекс i можно не указывать, если expr от него не зависит, так что минимальный формат цикла имеет вид: Do[expr, {imax}] – вычисления повторяются imax раз.
Do[ body, {i {i1, i2, i3, …}}] – для I используютя значения из списка значений.
Более общий формат команды: Do[body, {i, imin, imax}, {j, jmin, jmax}] – для каждого значения i вычисления повторяются при меняющихся значениях j.
Пример 7.3
Напишем еще одну программу вычисления “машинного эпсилон”:
In[ ]: = ep2=1.;Do[If[1.+ep2>1.,ep2=ep2/2,Break[]],{70}];2 ep2
Out[ ] = 2.84217*10-14
Алгоритм программы совпадает с алгоритмом предыдущей программы для вычисления машинного эпсилон, однако, поскольку цикл Do не содержит встроенной проверки условий выполнения операций цикла, программа включает условную функцию If. Eсли условие e2>1.0 выполнено, производятся действия цикла; как только условие нарушается, происходит выход из цикла по команде Break[ ].
7.4. Функция If
 Общий формат функции: If[test, then, else, unknown].Максимальное количество аргументов – четыре, но применимы также более короткие форматы: If[test, then, else] и If[test, then]. Если условие test выполнено, то вычисляется выражение then, иначе вычисляется else. Предусмотрен также случай, когда логическое значение условия test не может быть определено. Например, значение высказывания x<5 не определено, если не известно значение x. Более общая форма функции If учитывает эту возможность: если истинность условия test не определена, то вычисляется выражение unknown. Каждый из аргументов: then, else и unknown – может включать несколько операторов, отделенных друг от друга точкой с запятой. Функция If допускает вложения.
Общий формат функции: If[test, then, else, unknown].Максимальное количество аргументов – четыре, но применимы также более короткие форматы: If[test, then, else] и If[test, then]. Если условие test выполнено, то вычисляется выражение then, иначе вычисляется else. Предусмотрен также случай, когда логическое значение условия test не может быть определено. Например, значение высказывания x<5 не определено, если не известно значение x. Более общая форма функции If учитывает эту возможность: если истинность условия test не определена, то вычисляется выражение unknown. Каждый из аргументов: then, else и unknown – может включать несколько операторов, отделенных друг от друга точкой с запятой. Функция If допускает вложения.
Логические выражения
Язык пакета Математика содержит достаточное количество логических операторов, необходимых для составления условных выражений. Часть таких операторов приведена в таблице 7.1.
В таблице 7.2 приведены примеры логических выражений. Из высказываний, приведенных в первой строке, следует, что единица, записанная в формате чисел с плавающей запятой, равна единице, записанной в формате целых чисел, но не равна ей тождественно.
Значение высказывания во второй строчке таблицы определяется тем, что прибавляемое к единице число в левой части равенства меньше машинного эпсилон.
Значение высказывания в четвертой строке связано с тем, что в пакете Математика вводится особый формат чисел – Rational. В этом формате числа представляются точно, поэтому даже ничтожная прибавка к единице делает сумму отличной от единицы.



 Точка с запятой в конце выражения служит знаком запрета вывода результата на экран.
Точка с запятой в конце выражения служит знаком запрета вывода результата на экран.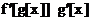 ,
,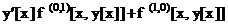 ,
, In[]:= D[x^3 / y, {x, 2}, y] Out[]= - 6x / y2.
In[]:= D[x^3 / y, {x, 2}, y] Out[]= - 6x / y2. Генераторы случайных чисел:
Генераторы случайных чисел: линейной зависимостью. Решение:
линейной зависимостью. Решение: f@x - префиксная форма (prefix form),
f@x - префиксная форма (prefix form), 6. Функции комплексного аргумента
6. Функции комплексного аргумента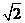
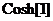
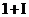 In[ ]: = Log[I] Out[] =
In[ ]: = Log[I] Out[] = 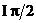
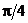
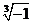 Математика просто переписывает в ином виде. Для упрощения выражений можно применить функцию ComplexExpand[expr] – вычисление всех степеней и произведений в выражении expr – либо где-нибудь в выражении expr поставить десятичную точку.
Математика просто переписывает в ином виде. Для упрощения выражений можно применить функцию ComplexExpand[expr] – вычисление всех степеней и произведений в выражении expr – либо где-нибудь в выражении expr поставить десятичную точку.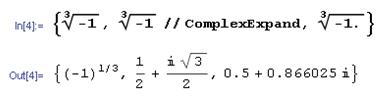
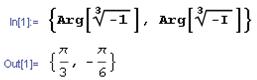 Найдем аргумент кубичного корня из –1 и –I. Запишем на языке пакета Математика:
Найдем аргумент кубичного корня из –1 и –I. Запишем на языке пакета Математика: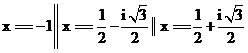 .
.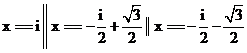 .
. Формат команды: For[start, test, incr, body]
Формат команды: For[start, test, incr, body] Общий формат функции: If[test, then, else, unknown].Максимальное количество аргументов – четыре, но применимы также более короткие форматы: If[test, then, else] и If[test, then]. Если условие test выполнено, то вычисляется выражение then, иначе вычисляется else. Предусмотрен также случай, когда логическое значение условия test не может быть определено. Например, значение высказывания x<5 не определено, если не известно значение x. Более общая форма функции If учитывает эту возможность: если истинность условия test не определена, то вычисляется выражение unknown. Каждый из аргументов: then, else и unknown – может включать несколько операторов, отделенных друг от друга точкой с запятой. Функция If допускает вложения.
Общий формат функции: If[test, then, else, unknown].Максимальное количество аргументов – четыре, но применимы также более короткие форматы: If[test, then, else] и If[test, then]. Если условие test выполнено, то вычисляется выражение then, иначе вычисляется else. Предусмотрен также случай, когда логическое значение условия test не может быть определено. Например, значение высказывания x<5 не определено, если не известно значение x. Более общая форма функции If учитывает эту возможность: если истинность условия test не определена, то вычисляется выражение unknown. Каждый из аргументов: then, else и unknown – может включать несколько операторов, отделенных друг от друга точкой с запятой. Функция If допускает вложения.


