Линейная зависимость векторов. Геометрический смысл линейной зависимости двух и трех векторов.
Вектор  называется линейной комбинацией векторов
называется линейной комбинацией векторов  ,
,  ,…,
,…,  , если он получен из этих векторов проведением над ними линейных операций его можно представить в виде
, если он получен из этих векторов проведением над ними линейных операций его можно представить в виде  , где
, где  ,
,  ,…,
,…,  − некоторые числа. Это равенство называют также разложением вектора
− некоторые числа. Это равенство называют также разложением вектора 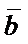 по векторам
по векторам  ,
,  ,…,
,…,  .
.
Векторы  ,
,  ,…,
,…,  являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например,
являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например,  . В противном случае (т.е. ни один из векторов
. В противном случае (т.е. ни один из векторов  ,
,  ,…,
,…,  не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.
не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.
Пара векторов на плоскости является линейно зависимой тогда и только тогда, когда эти векторы коллинеарные.
Тройка векторов в пространстве является линейно зависимой тогда и только тогда, когда эти векторы компланарны.
Необходимое и достаточное условие коллинеарности векторов
Для того что бы 2 не нулевых вектора были колинеларны необходимо и достаточно что бы они были линейно зависимы.
Необходимость:

Достаточность:

Необходимое и достаточное условие компланарности векторов:
Для того что бы 3 не нулевых вектора были компланарными необходимо и достаточно что бы они были линейно зависимы.
Необходимость: дано: 
Очевидно если хотя бы пара из них колинеарны, следовательно они компланарны т.е. линейно зависимы


Достаточность:

Формулы деления векторов в данном отношении.
Точка М делит отрезок АВ в отношении λ, если выполняется равенство  .
.
Если  ,
,  ,
,  , то
, то
 ,
,  ,
,  .
.
Особый интерес представляет случай, когда точка М делит отрезок АВ пополам. Тогда  =1 и координаты середины отрезка вычисляются по формулам
=1 и координаты середины отрезка вычисляются по формулам
 ,
,  ,
,  .
.
Скалярное произведение векторов.
Скалярным произведением двух векторов  и
и  называется число, равное произведению модулей этих векторов на косинус угла между ними
называется число, равное произведению модулей этих векторов на косинус угла между ними  .
.
Свойства скалярного произведения:
1)  (коммутативность);
(коммутативность);
2) 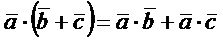 (дистрибутивность);
(дистрибутивность);
3)  , если
, если  или
или 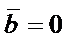 , или
, или 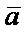 перпендикулярно
перпендикулярно  ;
;
4)  .
.
Первые три свойства показывают, что скалярное умножение суммы векторов на другую сумму можно производить по обычному правилу умножения многочленов.
Найдем выражение скалярного произведения векторов  и
и  в декартовых координатах. Для этого запишем разложение векторов
в декартовых координатах. Для этого запишем разложение векторов 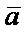 и
и  в базисе
в базисе 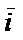 ,
,  ,
,  и с учетом свойства скалярного произведения получим
и с учетом свойства скалярного произведения получим


Учитывая, что
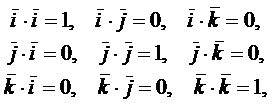
получим
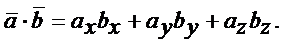
Таким образом, скалярное произведение равно сумме произведений одноименных координат.
Скалярное произведение векторов используется при решении ряда задач:
1) нахождение угла между векторами  и
и  :
:
 ;
;
2) вычисление проекции одного вектора на направление другого вектора:
 ;
;
3) проверка перпендикулярности двух векторов:

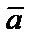 ׀
׀ 

 , т.е.
, т.е.  ;
;
4) вычисление работы постоянной силы  вдоль прямолинейного участка пути (вектор перемещения
вдоль прямолинейного участка пути (вектор перемещения  ):
):
 .
.
Определение точки пересечения прямой и плоскости


Для нахождения точки пересечения решаем систему из трех уравнений. Если решение единственное, то оно является корд. Точки пересечения. Если решений бесконечное мно-во, то прямая принадлежит плоскости. Если решений нет, то прямая не пересекается с плоскостью.
Скрещевающиесь прямые

Линейная зависимость векторов. Геометрический смысл линейной зависимости двух и трех векторов.
Вектор  называется линейной комбинацией векторов
называется линейной комбинацией векторов  ,
,  ,…,
,…,  , если он получен из этих векторов проведением над ними линейных операций его можно представить в виде
, если он получен из этих векторов проведением над ними линейных операций его можно представить в виде  , где
, где  ,
,  ,…,
,…,  − некоторые числа. Это равенство называют также разложением вектора
− некоторые числа. Это равенство называют также разложением вектора 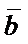 по векторам
по векторам  ,
,  ,…,
,…,  .
.
Векторы  ,
,  ,…,
,…,  являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например,
являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например,  . В противном случае (т.е. ни один из векторов
. В противном случае (т.е. ни один из векторов  ,
,  ,…,
,…,  не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.
не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.
Пара векторов на плоскости является линейно зависимой тогда и только тогда, когда эти векторы коллинеарные.
Тройка векторов в пространстве является линейно зависимой тогда и только тогда, когда эти векторы компланарны.



 называется линейной комбинацией векторов
называется линейной комбинацией векторов  ,
,  ,…,
,…,  , если он получен из этих векторов проведением над ними линейных операций его можно представить в виде
, если он получен из этих векторов проведением над ними линейных операций его можно представить в виде  , где
, где  ,
,  ,…,
,…,  − некоторые числа. Это равенство называют также разложением вектора
− некоторые числа. Это равенство называют также разложением вектора 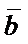 по векторам
по векторам  ,
,  ,…,
,…,  .
. ,
,  ,…,
,…,  являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например,
являются линейно зависимыми, если хотя бы один из них является линейной комбинацией остальных. Например,  . В противном случае (т.е. ни один из векторов
. В противном случае (т.е. ни один из векторов  ,
,  ,…,
,…,  не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.
не может быть представлен в виде линейной комбинации остальных) векторы являются линейно независимыми.





 .
. ,
,  ,
,  , то
, то ,
,  ,
,  .
. =1 и координаты середины отрезка вычисляются по формулам
=1 и координаты середины отрезка вычисляются по формулам ,
,  ,
,  .
. и
и  называется число, равное произведению модулей этих векторов на косинус угла между ними
называется число, равное произведению модулей этих векторов на косинус угла между ними  .
. (коммутативность);
(коммутативность);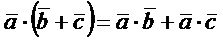 (дистрибутивность);
(дистрибутивность); , если
, если  или
или 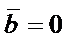 , или
, или 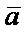 перпендикулярно
перпендикулярно  ;
; .
. и
и  в декартовых координатах. Для этого запишем разложение векторов
в декартовых координатах. Для этого запишем разложение векторов  в базисе
в базисе 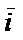 ,
,  ,
,  и с учетом свойства скалярного произведения получим
и с учетом свойства скалярного произведения получим

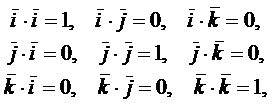
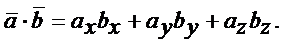
 и
и  :
: ;
; ;
;
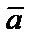 ׀
׀ 

 , т.е.
, т.е.  ;
; вдоль прямолинейного участка пути (вектор перемещения
вдоль прямолинейного участка пути (вектор перемещения  ):
): .
.




