Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...
Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
Топ:
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Интересное:
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Дисциплины:
 2017-12-12 |
 762 |
из
5.00
|
Заказать работу |
|
|
|
|
Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
|
Здесь x 1, x 2, …, xn — неизвестные, которые надо определить. a 11, a 12, …, amn — коэффициенты системы — и b 1, b 2, … bm — свободные члены — предполагаются известными. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[1].
Система (1) называется однородной, если все её свободные члены равны нулю (b 1 = b 2 = … = bm = 0), иначе — неоднородной.
Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.
Решение системы (1) — совокупность n чисел c 1, c 2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.
Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.
Совместная система вида (1) может иметь одно или более решений.
Решения c 1(1), c 2(1), …, cn (1) и c 1(2), c 2(2), …, cn (2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:
| c 1(1) = c 1(2), c 2(1) = c 2(2), …, cn (1) = cn (2). |
Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.
Метод Гаусса классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
|
|
Таким образом, процесс решения системы линейных алгебраических уравнений по методу Гаусса состоит из двух этапов. Первый этап (прямой ход метода) – система приводится к треугольному виду.Второй этап (обратный ход) – неизвестные определяются последовательно, начиная с последнего неизвестного и кончая первым.
Пример 2.13. Решить систему уравнений методом Гаусса:
x + y - 3z = 2,
3x - 2y + z = - 1,
2x + y - 2z = 0.
Решение. Выпишем расширенную матрицу данной системы
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
~ 
;
б) третью строку умножим на (-5) и прибавим к ней вторую:
.
В результате всех этих преобразований данная система приводится к треугольному виду:
x + y - 3z = 2,
-5y + 10z = -7,
- 10z = 13.
Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим
x = - 0,7.
8. Система линейных однородных уравнений.
Пусть дана система линейных однородных уравнений
Очевидно, что однородная система всегда совместна 
, она имеет нулевое (тривиальное) решение x1=x2=x3=...=xn=0.
Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r<n.
Необходимость:
Так как ранг не может превосходить размера матрицы, то, очевидно, r 
n. Пусть r=n. Тогда один из минеров размера nхn отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение:
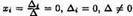
Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то r<n.
Достаточность:
Пусть r<n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения. Пусть дана однородная система n линейных уравнений с n неизвестными
|
|
Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель D был равен нулю, т. е. D=0.
Если система имеет ненулевые решения, то D=0. Ибо при D¹0 система имеет только единственное, нулевое решение. Если же D=0, то ранг r основной матрицы системы меньше числа неизвестных, т.е. r<n. И, значит, система имеет бесконечное множество (ненулевых) решений.
|
|
|
История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...
Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!