Случайная величина называется нормально распределенной, если ее плотность вероятности и функция распределения имеют вид:
 ,
,  ,
,
где  - функция Лапласа,
- функция Лапласа, 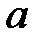 и
и  - параметры нормального распределения:
- параметры нормального распределения:
 (математическое ожидание),
(математическое ожидание),  (среднеквадратическое отклонение).
(среднеквадратическое отклонение).
Пример 15.
Прибор состоит из трех независимо работающих элементов. Вероятность отказа каждого элемента в одном испытании равна 0,2. Составить закон распределения числа отказавших элементов в одном опыте.
Решение.
Пусть случайная величина  - число отказавших деталей в одном опыте:
- число отказавших деталей в одном опыте:
 :
: 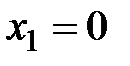 ,
,  ,
,  ,
,  .
.
Вероятность отказа указанного ( ) числа элементов вычисляется по формуле Бернулли, так как вероятности отказа каждого элемента равны между собой
) числа элементов вычисляется по формуле Бернулли, так как вероятности отказа каждого элемента равны между собой

 ,
,

 ,
,

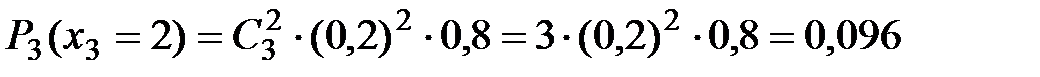 ,
,

 .
.
Проверим выполнение условия  :
:
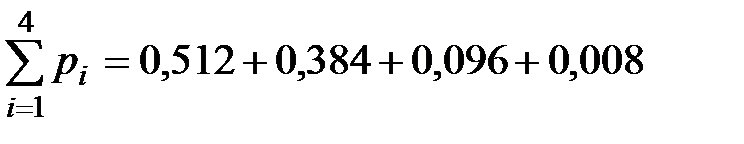 =1.
=1.
Составим ряд распределения случайной величины 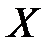 .
.

|
|
|
|
|

| 0,512
| 0,384
| 0,096
| 0,008
|
Пример 16.
Случайная величина  задана функцией распределения
задана функцией распределения  :
:

Найти функцию плотности распределения  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  , вычислить вероятность события
, вычислить вероятность события  , построить графики функций
, построить графики функций  и
и  .
.
Решение.
Функция плотность распределения 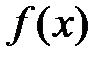 и функция распределения
и функция распределения  связаны равенством
связаны равенством  . Следовательно,
. Следовательно,

Построим график плотности распределения  :
:

Построим график функции распределения 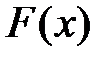 :
:

Найдем математическое ожидание  и дисперсию
и дисперсию  .
.
 ,
,
 .
.
События  и
и  противоположны, следовательно
противоположны, следовательно  , тогда
, тогда  .
.
Рассмотрим решение задач типового варианта.
Задание №1.
На полке стоят 10 книг, 7 из них по математике. Найти вероятность того, что среди 6-ти взятых наудачу книг 4 по математике.
Решение.
Пусть событие  – среди 6-ти взятых книг 4 по математике. Воспользуемся классическим определением вероятности. Искомая вероятность
– среди 6-ти взятых книг 4 по математике. Воспользуемся классическим определением вероятности. Искомая вероятность  равна отношению
равна отношению  – числа исходов, благоприятствующих событию
– числа исходов, благоприятствующих событию  , к
, к  – числу всех элементарных исходов:
– числу всех элементарных исходов:
 .
.
Общее число всех всевозможных элементарных исходов испытания равно числу способов, которыми можно извлечь 6 книг из 10 имеющихся, т.е. числу сочетаний из 10 элементов по 6 ( ).
).
Определим  – число исходов, благоприятствующих событию
– число исходов, благоприятствующих событию  . Четыре книги можно взять из 7 книг по математике
. Четыре книги можно взять из 7 книг по математике  способами; при этом остальные (
способами; при этом остальные ( ) книги должны быть не по математике. Взять же 2 книги нематематические из (
) книги должны быть не по математике. Взять же 2 книги нематематические из ( ) нематематических книг можно
) нематематических книг можно  способами. Следовательно, число благоприятствующих исходов
способами. Следовательно, число благоприятствующих исходов  . Таким образом, учитывая, что
. Таким образом, учитывая, что  , получаем:
, получаем:
 .
.
Ответ:  .
.
Задание №2.
Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна  , а для второго –
, а для второго –  . Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
Решение.
Пусть событие  – попадание в цель первым стрелком, событие
– попадание в цель первым стрелком, событие  – вторым, промах первого стрелка – событие
– вторым, промах первого стрелка – событие  , промах второго – событие
, промах второго – событие  . Тогда
. Тогда  ,
,  ,
,  ,
,  .
.
Вероятность того, что первый стрелок попадет в мишень, а второй – нет, равна  . Вероятность того, что второй стрелок попадет в цель, а первый – нет, равна
. Вероятность того, что второй стрелок попадет в цель, а первый – нет, равна  . Тогда вероятность попадания в цель только одним стрелком равна
. Тогда вероятность попадания в цель только одним стрелком равна  .
.
Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:  ;
; 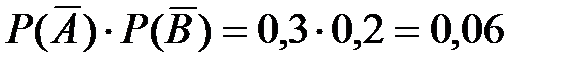 . Тогда вероятность того, что в цель попадет только один стрелок равна:
. Тогда вероятность того, что в цель попадет только один стрелок равна: 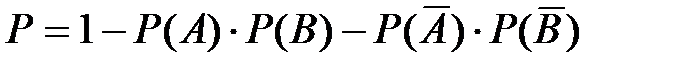
 .
.
Ответ:  .
.
Задание №3.
Изделия, производимые предприятием, попадают для проверки к двум контролерам. Вероятность того, что изделия попадут первому контролеру равна -  , а второму -
, а второму -  . Вероятность того, что бракованное изделие будет признано годным первым контролером равна
. Вероятность того, что бракованное изделие будет признано годным первым контролером равна  , а вторым -
, а вторым - 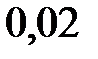 . Бракованное изделие было признано при приемке годным. Найти вероятность того, что бракованное изделие проверял первый контролер.
. Бракованное изделие было признано при приемке годным. Найти вероятность того, что бракованное изделие проверял первый контролер.
Решение.
Пусть событие 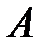 – бракованное изделие признано годным. Это событие может произойти при реализации одной из двух 2-х гипотез:
– бракованное изделие признано годным. Это событие может произойти при реализации одной из двух 2-х гипотез:  – изделие проверил первый контролер,
– изделие проверил первый контролер,  – изделие проверил второй контролер. Легко заметить, что эти гипотезы образуют полную группу событий и их вероятности по условию равны
– изделие проверил второй контролер. Легко заметить, что эти гипотезы образуют полную группу событий и их вероятности по условию равны 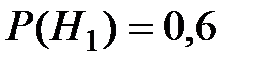 ,
,  .
.
В свою очередь, вероятность события  при условии реализации гипотезы
при условии реализации гипотезы  равна
равна  , а при условии реализации гипотезы
, а при условии реализации гипотезы  равна
равна  .
.
Определим вероятность реализации гипотезы  при условии, что событие
при условии, что событие  произошло, используя для этого формулу Байеса:
произошло, используя для этого формулу Байеса:
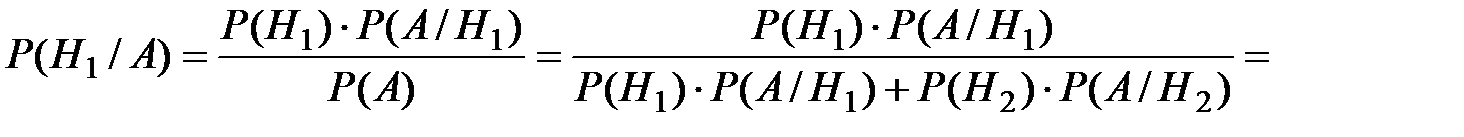

Ответ:  .
.
Задание №4.
По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела  . Найти вероятность того, что в цель попали не менее 3-х раз.
. Найти вероятность того, что в цель попали не менее 3-х раз.
Решение.
Пусть событие  – попадание в цель,
– попадание в цель,  – промах. По условию
– промах. По условию  , следовательно
, следовательно  . Можно считать, что производится 5 независимых испытаний (5 выстрелов). Поэтому будем использовать формулу Бернулли:
. Можно считать, что производится 5 независимых испытаний (5 выстрелов). Поэтому будем использовать формулу Бернулли:
 ,
,
 ,
,  ,
,  . Учитывая, что
. Учитывая, что
 ,
,
имеем


Ответ:  .
.
Задание №5.
Предприятие выпускает 20% изделий 2-го сорта. Найти вероятность того, что среди случайно отобранных  изделий окажется от 70-ти до 100 изделий 2-го сорта.
изделий окажется от 70-ти до 100 изделий 2-го сорта.
Решение.
Пусть событие  – проверяемое изделие 2-го сорта. Тогда
– проверяемое изделие 2-го сорта. Тогда  . Получаем схему Бернулли, где
. Получаем схему Бернулли, где  ,
,  .
.
Требуется найти  . Поскольку
. Поскольку  велико, применим интегральную формулу Муавра-Лапласа:
велико, применим интегральную формулу Муавра-Лапласа:
 , где
, где  ,
,  .
.
Вычислим:
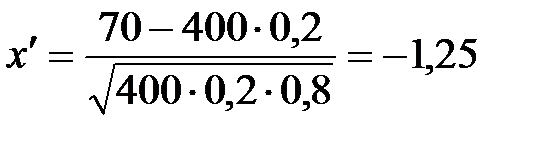 ,
,  .
.
Таким образом, имеем:
 .
.
По таблице 4 значений функции 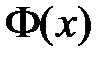 находим, что:
находим, что:

Следовательно,
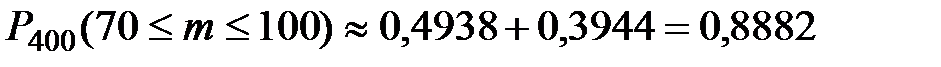 .
.
Ответ:  .
.
Задание №6.
На факультете учатся 300 студентов. Найти вероятность того, что 31 декабря является днем рождения: а) 2-х студентов; б) не менее 2-х студентов.
Решение.
Пусть событие  – случайно выбранный студент родился 31 декабря. Получаем схему Бернулли, где
– случайно выбранный студент родился 31 декабря. Получаем схему Бернулли, где  ,
,  . Поскольку
. Поскольку  велико, а
велико, а  – мало и
– мало и  , то воспользуемся формулой Пуассона, где
, то воспользуемся формулой Пуассона, где  .
.
а)  (по таблице 1);
(по таблице 1);
б)  (по таблице 2).
(по таблице 2).
Ответ:  ;
;  .
.
Задание №7.
В коробке 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают обратно и шары перемешивают. Приняв за случайную величину  - число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.
- число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.
Решение.
Т.к. шары в каждом опыте возвращаются обратно и перемешиваются, то испытания можно считать независимыми (результат предыдущего опыта не влияет на вероятность появления или не появления события в другом опыте). Таким образом, вероятность появления белого шара в каждом опыте постоянна и равна  , соответственно, вероятность появления черного шара
, соответственно, вероятность появления черного шара  . Значит, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз. Для составления закона распределения надо найти вероятности каждого из этих событий. Для этого будем использовать формулу Бернулли
. Значит, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз. Для составления закона распределения надо найти вероятности каждого из этих событий. Для этого будем использовать формулу Бернулли  .
.
1) Белый шар не появился вовсе:  .
.
2) Белый шар появился один раз:  .
.
3) Белый шар появиться два раза: 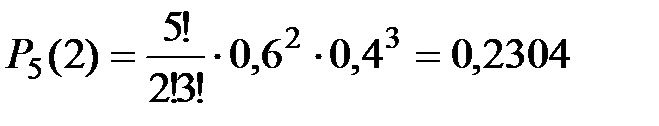 .
.
4) Белый шар появиться три раза:  .
.
5) Белый шар появиться четыре раза:  .
.
6) Белый шар появился пять раз: 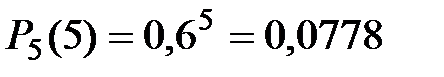 .
.
Получаем закон распределения случайной величины  .
.

|
|
|
|
|
|
|

|
|
|
|
|
|
|

| 0,0102
| 0,0768
| 0,2304
| 0,3456
| 0,2592
| 0,0778
|
Найдем математическое ожидание  :
:
 .
.
Вычислим дисперсию 
 ,
,

 ,
,
 .
.
Ответ:  ;
;  .
.
Задание №8.
Непрерывная случайная величина задана функцией распределения  :
:

Определить коэффициент  , найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина
, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина  попадет в интервал
попадет в интервал 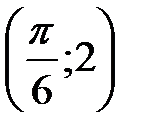 . Найти математическое ожидание и дисперсию.
. Найти математическое ожидание и дисперсию.
Решение.
Найдем коэффициент  , используя свойство функции плотности распределения
, используя свойство функции плотности распределения 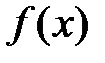 :
:  .
.
 .
.
Итак,  . Найдем функцию распределения:
. Найдем функцию распределения:
1) на интервале  :
:  ;
;
2) на интервале  :
:
 ;
;
3) на интервале  :
:
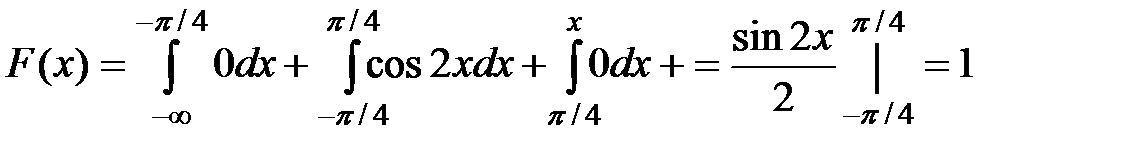 .
.
Таким образом,

 ;
;
Построим график плотности распределения  :
:
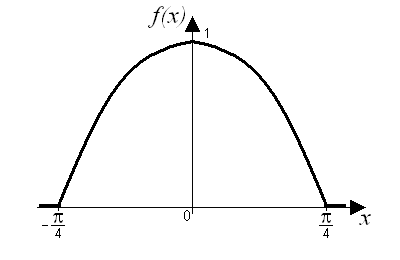
Построим график функции распределения  :
:

Найдем вероятность попадания случайной величины  в интервал
в интервал 
 .
.
Вероятность можно найти и другим способом:
 .
.
Вычислим математическое ожидание  .
.

Найдем дисперсию  .
.
 ,
,

 .
.
Ответ:  ;
;  ,
,  ,
,
 ,
, 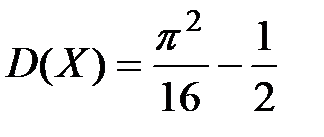 .
.
Задание №9.
Нормально распределенная величина  задана своими параметрами: математическое ожидание
задана своими параметрами: математическое ожидание  и среднеквадратическое отклонение
и среднеквадратическое отклонение  . Найти вероятность того, что а) значения случайной величины попадут в интервал
. Найти вероятность того, что а) значения случайной величины попадут в интервал  , б) случайная величина
, б) случайная величина  отклонится по модулю от математического ожидания не более чем на
отклонится по модулю от математического ожидания не более чем на  .
.
Решение.
а) Так как случайная величина  распределена по нормальному закону, то вероятность, что значения этой случайной величины попадут в интервал
распределена по нормальному закону, то вероятность, что значения этой случайной величины попадут в интервал  , находится по формуле:
, находится по формуле:
 ,
,
где  - математическое ожидание,
- математическое ожидание, 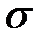 - среднеквадратическое отклонение, а значения функции
- среднеквадратическое отклонение, а значения функции  находим по таблице 4.
находим по таблице 4.

б) Вероятность, что нормально распределенная величина  отклонится по модулю от математического ожидания
отклонится по модулю от математического ожидания 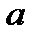 не более чем на
не более чем на  находится по формуле:
находится по формуле:

 .
.
Ответ: а)  , б)
, б)  .
.
ФОРМУЛА БАЙЕСА
Основные определения и формулы
Случайным событием называется такое событие, которое может произойти или не произойти в результате некоторого опыта.
Случайные события называют несовместными в данном испытании, если появление одного из них исключает появление других событий в одном и том же испытании.
Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие несовместное с ними.
Вероятностью Р события А называется отношение числа m благоприятствующих случаев к числу всех возможных случаев

(1)
Сумма вероятностей случайных событий B1, B2,…Bn,

образующих полную группу, равна единице
Событие А называется зависимым от события В, если вероятность появления события А зависит от того, произошло или не произошло событие В.

Вероятность того, что произошло событие А при условии,что произошло событие В, будем обозначать P(A/B) и называть условной вероятностью события А при условии В.
Рассмотрим полную группу несовместных событий В1, В2, …, Вn, вероятности появления которых P(B1), P(B2), …, P(Bn). Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Событие А может наступить в каком-либо опыте вместе с одной из гипотез событий В1, В2, …, Вn. Вероятность события А вычисляется по формуле полной вероятности

(2)

После опыта (апостериорно) стало известно, что событие А появилось, следует выяснить, вместе с какой из гипотез B1,…, Bn оно произошло. По постановке задача напоминает диагностику причины по известному следствию.
P(Bi), i=1,…n - априорные (доопытные) вероятности гипотез
P(Bi / A), i=1,…n - апостериорные вероятности гипотез (сформировавшиеся после опыта)
Найдем апостериорные вероятности гипотез P(Bi / A), i=1,…n.
По формуле умножения вероятностей найдем вероятность совмещения событий B и А
P(Bi A)=P(Bi) P(A / Bi)=P(A) P(Bi/A).
Из последнего равенства выразим апостериорную вероятность гипотезы В

(3)
Получили формулы Байеса. Формулы Байеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, т.е. провести коррекцию вероятностей априорных гипотез, используя экспериментальные данные.
I. Задача.
Имеются три одинаковые на вид урны. В первой урне – 2 белых и 1 черный шар, во второй – 3 белых и 1 черный, в третьей – 2 белых и 2 черных. Некто наудачу вынимает шар из урны. Найти вероятность того, что шар белый.
Решение. Событие А – извлечение белогошара.
Выдвинем гипотезы:
B1 – шар выбран из первой урны;
B2 – шар выбран из второй урны;
B3 – шар выбран из третьй урны.
Гипотезы равновероятны, т.е. во всех случаях m=1, n=3.
P(B1)=P(B2)=P(B3)=1/3.
Вероятность извлечения белого шара из первой урны –условную вероятность - найдем по формуле классического определения вероятности (формула (1)), если m=2, n=3, P(А/B1)=2/3;
из второй урны - m=3, n=4, P(А/B2)=3/4;
из третьей урны - m=2, n=4, P(А/B3)=2/4;
По формуле полной вероятности (2) находим вероятность появления события А
Р(А)=1/3*2/3+1/3*3/4+1/3*1/2.
Пусть теперь событие А произошло - из урны извлечен белый шар.
Найдем вероятность того, что этот шар извлечен из первой урны Р(В1/А) по формуле (3).
Р(В1/А)=(1/3*2/3)/Р(А).
Вычисления выполним на компьютере в программе EXCEL.
Для запуска программы EXCEL щелкнуть на кнопке Пуск-Программы –Microsoft Excel.
Выполнение работы.
1.В столбце А выделить ячейку А1, для этого подвести курсор мыши к ячейке и щелкнуть левой клавишей мыши. Записать с клавиатуры в ячейке А1 заголовок гипотезы Вi, нажать клавишу ENTER, ячейку A2 выделить, записать - В1, повторить для В2, В3. Чтобы разместить заголовок в две строки (или больше строк), нажмите клавиши ALT+ ENTER в том месте текста, где вы хотите перейти на другую строку. (Рис. 1).

Рис.1.
2. В столбце В записать: 1) заголовок в ячейке В1 - данные для расчета вероятностей гипотез( см.п.1), нажатием клавиши ENTER перейти к В2;
(Заголовок занимает ячейки В1-Е1. Объединение ячеек заголовка выполняется следующим образом: выделить мышью ячейки, содержащие текст; использовать команду меню Формат – Ячейки – Выравнивание.. В открывшемся окне щелчком мыши поставить точку – напротив окна центрировать по выделению.)
2) в ячейке В2записать символы n=.
3. Выделить ячейку С2, записать число, равное значению n ( см.п.1).
4. Выделить ячейку D2 ( см.п.1), записать заголовок m1=, в ячейках D3, D4 соответственно записать заголовки m2=, m3=.
5. В ячейках Е2-Е4 записать соответствующие значения mi.
6. В столбце G 1) в ячейке G1 записать заголовок данные для расчета у словных вероятностей Р(Вi/А), 2) в ячейках G2 – G4 записать соответственно n1=, n2=, n3= (Рис. 2).

Рис.2.
7. В ячейках Н2 - Н4 записать соответствующие значения ni.
8. В ячейках I2 – I4 записать m1=, m2=, m3=.
9. В ячейках J2 - J4 записать соответствующие значения mi.
10. В столбце F выделить ячейку F1, записать заголовок Р(Вi), нажав клавишу ENTER перейти к ячейке F2, рассчитать вероятность гипотезы В1 по формуле (1). Для этого щелкнуть мышью на ячейке В2 и вычислить значение вероятности (равное 1 /3), т.е. набрать на клавиатуре знак =, щелкнуть мышью на ячейке Е2, содержащей значение m1, набрать знак деления /, щелкнуть мышью на ячейке С2, содержащей значение n, нажатием клавиши ENTER получить результат. (Проследите, чтобы в ячейке F2 была записана формула =Е2/С2.) В ячейках F3, F4 рассчитать вероятности аналогично (Рис. 3).
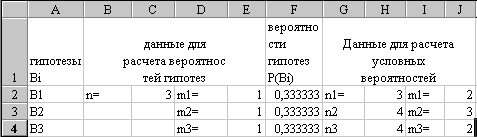
Рис.3.
11. В столбце K записать:1) в ячейке K1 заголовок условные вероятности P(A/Bi); 2) в ячейках K2 – K4 вычислить условные вероятности P(A/Bi) по формуле (1), т.е. в ячейке K2 набрать формулу =J2/H2 (см.п.10), в ячейках K3, K4 рассчитать условные вероятности аналогично.
12. В столбце L записать 1) в ячейке L1 заголовок полная вероятность P(A); 2) в ячейке L2 вычислить значение полной вероятности по формуле (2), щелкнуть мышью на ячейке L2, набрать формулу =F2*L2+F3*L3+F4*L4, нажатием клавиши ENTER получить результат (Рис. 4).
13. В столбце M записать 1) в ячейке M1 заголовок апостериорная вероятность P(Bi/A); 2) в ячейках M2-M4 вычислить значения апостериорных вероятностей P(Bi/A) по

Рис.4
формулам (3), выделить ячейку M2, набрать формулу =F2*K2/L2, нажатием клавиши ENTER получить результат (Рис.5).
Большее число в ячейках M2-M4 укажет более вероятную гипотезу.

14. Выбрать из полученных чисел наибольшее. Наиболее вероятную гипотезу и ее вероятность выделить жирным шрифтом.. (Для того, чтобы выделить всю строку, щелкните по номеру строки).
Рис. 5.
Для решения аналогичных задач достаточно изменить значения n и m в столбцах С, Е, H, J. При этом количество несовместных событий – гипотез Вi - должно соответствовать смыслу задачи.
II. Решить задачи, используя таблицу.
I уровень:
При отклонении от нормального режима работы автомата сигнализатор С-1 реагирует на сбой в 50 случаях 40 раз, а сигнализатор С-11 – в 50 случаях 50 раз. Из 10 автоматов снабжены сигнализатором С-1 - 6, а сигнализатором С-11 - 4. Получен сигнал от автомата. Что вероятнее: автомат снабжен сигнализатором С-1 или С-11?
II уровень:
Событие А может появиться при условии появления одного из несовместных событий (гипотез) B1, B2, B3, образующих полную группу событий. После появления события А произошло перераспределение вероятностей, были найдены условные вероятности гипотез Р(А/В1)=0,6; Р(А/В2)=0,3. Чему равна условная вероятность гипотезы В3?
Два из трех независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов равны соответственно 0,2; 0,4; 0,3.
ЗАДАЧИ И УПРАЖНЕНИЯ
1. При игре в кости бросаются два игральных кубика и подсчитывается сумма выпавших очков. Найти вероятность событий: А - сумма равна 5; В - сумма равна 7.
Ответ: Р(А) = 0,1111, Р(В) = 0,1667
2. Из имеющихся 15 телевизоров 10 готовы к продаже, а 5 требуют дополнительной регулировки. Найти вероятности событий: А - из случайно отобранных трёх телевизоров все хорошие, В - два хорошие и один нет, С - один хороший и два нет, D - хороших нет.
Ответ: Р(А) = 0,2637, Р(В) = 0,4945, Р(С) = 0,2198, Р(D) = 0,022.
3. Из изготовленных N изделий M стандартные (M £ N). Найти вероятность того, что из n случайно отобранных изделий ровно m стандартные (m £ n).
Ответ: Р(А) =  .
.
4. В студенческой группе из 30 студентов 20 успевают на хорошо и отлично, 5 - удовлетворительно и остальные плохо. Найти вероятность того, что из пяти случайно отобранных студентов: А - все успевают на хорошо и отлично; В - 3 хорошо и отлично, 1 удовлетворительно и 1 плохо; С - 3 удовлетворительно и 2 плохо.
Ответ: Р(А) =0,1088, Р(В) = 0,2, Р(С) = 0,0007.
5. В книжной лотерее разыгрываются 30 билетов, из них 10 - выигрышные. Определить вероятность того, что из двух купленных билетов окажутся: А - оба выигрышные, В - один выигрышный, другой нет; С - оба проигрышные.
Ответ: Р(А) = 0,1034, Р(В) = 0,4598, Р(С) = 0,4368.
6. Абонент забыл три цифры нужного ему телефонного номера и набирает их наудачу. Найти вероятность того, что номер будет набран правильно, если: А - абонент помнит, что все эти цифры различные, В - ничего не помнит об этих цифрах.
Ответ: Р(А) = 0,0014, Р(В) = 0,001.
7. Две бригады получили 10 инструментов, из которых 2 новых и 8 старых. Найти вероятность того, при делении их случайным образом каждой бригаде достанется 1 новый и 4 старых.
Ответ: Р(А) =0,5556.
8. В лотерее разыгрывается 30 билетов, из них 5 “счастливые”. Найти вероятность того, что из 4 купленных случайным образом билетов 2 будут счастливыми.
Ответ: Р(А) = 0,1095.
9. В спортлото (5 из 36) надо отметить 5 чисел из 36. Найти вероятность того, что случайным образом удастся угадать: 0, 1, 2, 3, 4, 5 пять чисел из пять заранее выбранных (но не известных играющему) чисел.
Ответ: Р(0) = 0,4507, Р(1) = 0,4173, Р(2) = 0,1192, Р(3) = 0,01233,
Р(4) = 0,0004111, Р(5) = 0,000002653.
10. Рассматриваются всевозможные пятизначные числа. Найти вероятность того, что: А - случайно выбранное число записано различными цифрами; В - не содержит цифры 5.
Ответ: Р(А) = 0,3024, Р(В) = 0,5832.
11. Студенческая группа состоит из 15 юношей и 4 девушек. По жребию (случайным образом) выбирают 4 дежурных. Найти вероятность того, что будут выбраны 2 девушки и 2 юноши.
Ответ: Р(А) = 0,1625
12. В партии из 20 часов 3 дефектные. Найти вероятность того, что из 4 случайно купленных часов все хорошие.
Ответ: Р(А) = 0,4912.
13. Имеются два цифровых замка. На первом размещено 6 дисков, на каждом из которых находится 5 символов; на втором - 5 дисков с 6 символами на каждом. Какой из них лучше?
Ответ: Р(А) = 0,000064 < Р(В) = 0,000129 (первый лучше).
14. Буквы, составляющие слово РЕМОНТ выписаны каждая на отдельной карточке и тщательно перемешаны. Найти вероятность того, что: А - при последовательном отборе четырёх карточек сразу получится слово МОРЕ; В - из отобранных карточек можно составить это слово.
Ответ: Р(А) = 0,002778, Р(В) = 0,06667.
15. На четырёх карточках выписаны две буквы М и две буквы А. Найти вероятность того, что при случайном отборе карточек сразу получится слово МАМА.
Ответ: Р(А) =0,1667.
16. Буквы, составляющие слово ОДЕССА выписаны на отдельных карточках и тщательно перемешаны. Найти вероятность того, что при последовательном отборе трёх карточек появятся буквы составляющие слова: А - САД, В - АСС, С - ОСА; D - четырех карточек - слово СОДА.
Ответ: Р(А) = 0,0167, Р(В) = 0,0167, Р(С) = 0,0167, Р(D) = 0,0056.
17. Решить предыдущую задачу считая, что по извлечённой карточке записывается буква, а сама карточка возвращается и все карточки снова тщательно перемешиваются.
Ответ: Р(А) = 0,0093, Р(В) = 0,0185, Р(С) = 0,0093, Р(D) = 0,0015.
18. Сетка с прямоугольными ячейками сварена из прутков диаметром 1см, с горизонтальным шагом 10 и вертикальным - 15см. Найти вероятность того, что шарик радиуса 1см, брошенный не прицельно, перпендикулярно сетке, пройдёт через неё без столкновений.
Ответ: Р(А) =0,56.
19. Перпендикулярно фарватеру установлен один ряд мин, расстояние между которыми равно 100 метров. Найти вероятность того, что: А - судно с наибольшей шириной 30м пройдёт линию заграждения без столкновения с миной; В - судно будет двигаться под углом 30о к фарватеру?
Ответ: Р(А) = 0,7, Р(В) = 0,6564.
20. На отрезок АВ длины L брошена точка М так, что её любое положение на отрезке равновозможно. Найти вероятность того, что меньший из отрезков (АМ или МВ) имеет длину, большую чем L\3.
Ответ: Р(А) = 0,3333.
21. Плоскость разделена параллельными прямыми на полосы шириной 10см каждая. На плоскость случайным образом брошен круг радиуса 2см. Найти вероятность того, что круг не пересечёт прямые.
Ответ: Р(А) = 0,6.
22. На отрезок АВ длины L брошены точки М и N так, что любое их положение на этом отрезке равновозможно. Найти вероятность того, что длина отрезка MN меньше длины наименьшего из отрезков АМ или АN.
Ответ: Р(А) = 0,5.
23. Задача о встрече. Два студента М и Д договорились встретиться в определённом месте между 18 и 19 часами. Если первым приходит М, то он ждёт не более 20 минут и затем уходит, если первой приходит Д, то ждёт не более 10 минут. Найти вероятность того, что встреча состоится, если каждый из них выбирает момент своего прихода наудачу.
Ответ: Р(А) = 0,4306.
24. Пол выложен прямоугольными плитками размерами 15 на 20см. Найти вероятность того, что брошенная на пол случайным образом монета (круг радиуса 2см) не пересечёт границ одной плитки.
Ответ: Р(А) = 0,5867.
 25. В круг случайным образом брошена точка так, что любое её положение в круге равновозможно. Найти вероятность того, что она окажется внутри: А - вписанного в круг квадрата; В - вписанного в круг равностороннего треугольника.
25. В круг случайным образом брошена точка так, что любое её положение в круге равновозможно. Найти вероятность того, что она окажется внутри: А - вписанного в круг квадрата; В - вписанного в круг равностороннего треугольника.
Ответ: Р(А) = 0,6366, Р(В) = 0,4135.
26. Опыт заключается в случайном бросании точки на квадрат (достоверное событие W), а попадание точки в области А, В и С - есть события А, В и С. Указать (заштриховать соответствующую область) события:  ;
; 
|
|
|



 ,
,  ,
, - функция Лапласа,
- функция Лапласа, 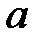 и
и  - параметры нормального распределения:
- параметры нормального распределения: (математическое ожидание),
(математическое ожидание),  (среднеквадратическое отклонение).
(среднеквадратическое отклонение). - число отказавших деталей в одном опыте:
- число отказавших деталей в одном опыте: :
: 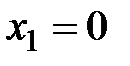 ,
,  ,
,  ,
,  .
. ) числа элементов вычисляется по формуле Бернулли, так как вероятности отказа каждого элемента равны между собой
) числа элементов вычисляется по формуле Бернулли, так как вероятности отказа каждого элемента равны между собой
 ,
,
 ,
,
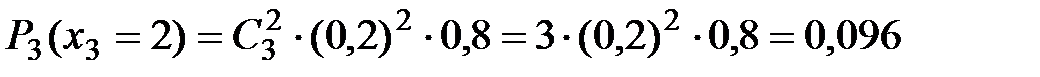 ,
,
 .
. :
: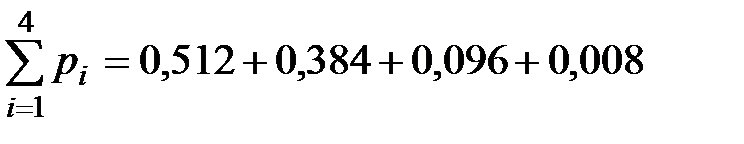 =1.
=1.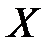 .
.

 задана функцией распределения
задана функцией распределения  :
:
 , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  , вычислить вероятность события
, вычислить вероятность события  , построить графики функций
, построить графики функций  и
и  .
.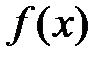 и функция распределения
и функция распределения  связаны равенством
связаны равенством  . Следовательно,
. Следовательно,
 :
:
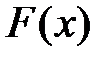 :
:
 и дисперсию
и дисперсию  .
. ,
, .
. и
и  противоположны, следовательно
противоположны, следовательно  , тогда
, тогда  .
. – среди 6-ти взятых книг 4 по математике. Воспользуемся классическим определением вероятности. Искомая вероятность
– среди 6-ти взятых книг 4 по математике. Воспользуемся классическим определением вероятности. Искомая вероятность  равна отношению
равна отношению  – числа исходов, благоприятствующих событию
– числа исходов, благоприятствующих событию  , к
, к  – числу всех элементарных исходов:
– числу всех элементарных исходов: .
. ).
). – число исходов, благоприятствующих событию
– число исходов, благоприятствующих событию  . Четыре книги можно взять из 7 книг по математике
. Четыре книги можно взять из 7 книг по математике  способами; при этом остальные (
способами; при этом остальные ( ) книги должны быть не по математике. Взять же 2 книги нематематические из (
) книги должны быть не по математике. Взять же 2 книги нематематические из ( ) нематематических книг можно
) нематематических книг можно  способами. Следовательно, число благоприятствующих исходов
способами. Следовательно, число благоприятствующих исходов  . Таким образом, учитывая, что
. Таким образом, учитывая, что  , получаем:
, получаем: .
. .
. , а для второго –
, а для второго –  . Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков. – попадание в цель первым стрелком, событие
– попадание в цель первым стрелком, событие  – вторым, промах первого стрелка – событие
– вторым, промах первого стрелка – событие  , промах второго – событие
, промах второго – событие  . Тогда
. Тогда  ,
,  ,
,  ,
,  .
. . Вероятность того, что второй стрелок попадет в цель, а первый – нет, равна
. Вероятность того, что второй стрелок попадет в цель, а первый – нет, равна  . Тогда вероятность попадания в цель только одним стрелком равна
. Тогда вероятность попадания в цель только одним стрелком равна  .
. ;
; 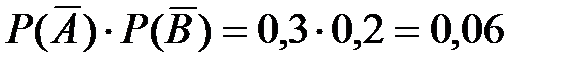 . Тогда вероятность того, что в цель попадет только один стрелок равна:
. Тогда вероятность того, что в цель попадет только один стрелок равна: 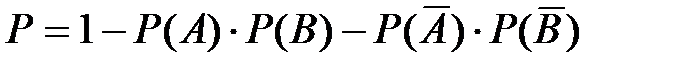
 .
. .
. , а второму -
, а второму -  . Вероятность того, что бракованное изделие будет признано годным первым контролером равна
. Вероятность того, что бракованное изделие будет признано годным первым контролером равна  , а вторым -
, а вторым - 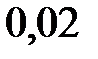 . Бракованное изделие было признано при приемке годным. Найти вероятность того, что бракованное изделие проверял первый контролер.
. Бракованное изделие было признано при приемке годным. Найти вероятность того, что бракованное изделие проверял первый контролер.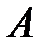 – бракованное изделие признано годным. Это событие может произойти при реализации одной из двух 2-х гипотез:
– бракованное изделие признано годным. Это событие может произойти при реализации одной из двух 2-х гипотез:  – изделие проверил первый контролер,
– изделие проверил первый контролер,  – изделие проверил второй контролер. Легко заметить, что эти гипотезы образуют полную группу событий и их вероятности по условию равны
– изделие проверил второй контролер. Легко заметить, что эти гипотезы образуют полную группу событий и их вероятности по условию равны 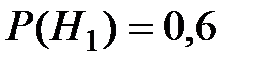 ,
,  .
. при условии реализации гипотезы
при условии реализации гипотезы  равна
равна  , а при условии реализации гипотезы
, а при условии реализации гипотезы  равна
равна  .
. при условии, что событие
при условии, что событие  произошло, используя для этого формулу Байеса:
произошло, используя для этого формулу Байеса: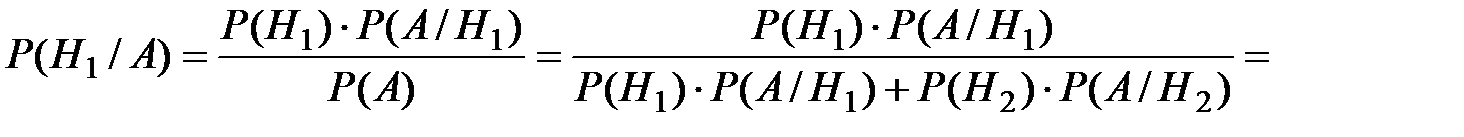

 .
. . Найти вероятность того, что в цель попали не менее 3-х раз.
. Найти вероятность того, что в цель попали не менее 3-х раз. – попадание в цель,
– попадание в цель,  – промах. По условию
– промах. По условию  , следовательно
, следовательно  . Можно считать, что производится 5 независимых испытаний (5 выстрелов). Поэтому будем использовать формулу Бернулли:
. Можно считать, что производится 5 независимых испытаний (5 выстрелов). Поэтому будем использовать формулу Бернулли: ,
, ,
,  ,
,  . Учитывая, что
. Учитывая, что ,
,

 .
. изделий окажется от 70-ти до 100 изделий 2-го сорта.
изделий окажется от 70-ти до 100 изделий 2-го сорта. – проверяемое изделие 2-го сорта. Тогда
– проверяемое изделие 2-го сорта. Тогда  . Получаем схему Бернулли, где
. Получаем схему Бернулли, где  ,
,  .
. . Поскольку
. Поскольку  велико, применим интегральную формулу Муавра-Лапласа:
велико, применим интегральную формулу Муавра-Лапласа: , где
, где  ,
,  .
.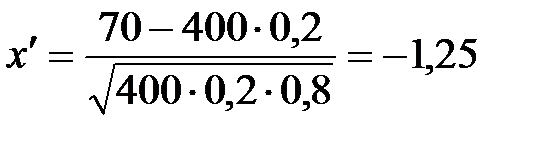 ,
,  .
. .
.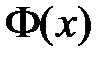 находим, что:
находим, что:
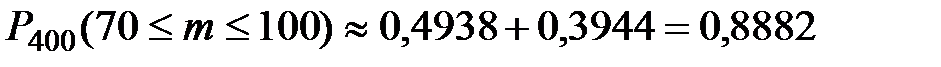 .
. .
. – случайно выбранный студент родился 31 декабря. Получаем схему Бернулли, где
– случайно выбранный студент родился 31 декабря. Получаем схему Бернулли, где  ,
,  . Поскольку
. Поскольку  велико, а
велико, а  – мало и
– мало и  , то воспользуемся формулой Пуассона, где
, то воспользуемся формулой Пуассона, где  .
. (по таблице 1);
(по таблице 1); (по таблице 2).
(по таблице 2). ;
;  .
. - число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию.
- число извлеченных белых шаров, составить закон распределения этой величины, определить ее математическое ожидание и дисперсию. , соответственно, вероятность появления черного шара
, соответственно, вероятность появления черного шара  . Значит, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз. Для составления закона распределения надо найти вероятности каждого из этих событий. Для этого будем использовать формулу Бернулли
. Значит, в результате пяти последовательных испытаний белый шар может не появиться вовсе, появиться один раз, два, три, четыре или пять раз. Для составления закона распределения надо найти вероятности каждого из этих событий. Для этого будем использовать формулу Бернулли  .
. .
. .
.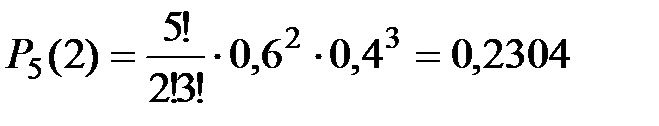 .
. .
. .
.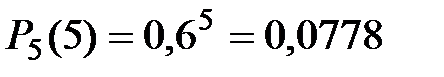 .
. .
.


 :
: .
.
 ,
,
 ,
, .
. ;
;  .
. :
:
 , найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина
, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина  попадет в интервал
попадет в интервал 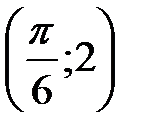 . Найти математическое ожидание и дисперсию.
. Найти математическое ожидание и дисперсию. , используя свойство функции плотности распределения
, используя свойство функции плотности распределения 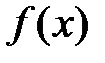 :
:  .
. .
. . Найдем функцию распределения:
. Найдем функцию распределения: :
:  ;
; :
: ;
; :
: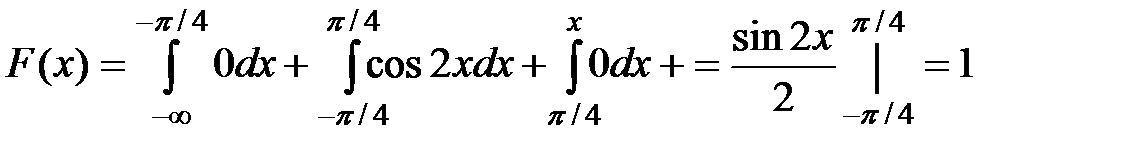 .
.
 ;
; :
:
 :
:
 в интервал
в интервал 
 .
. .
. .
.
 .
. ,
,
 .
. ;
;  ,
,  ,
, ,
, 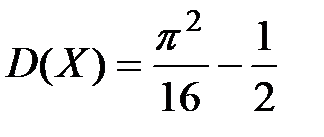 .
. задана своими параметрами: математическое ожидание
задана своими параметрами: математическое ожидание  и среднеквадратическое отклонение
и среднеквадратическое отклонение  . Найти вероятность того, что а) значения случайной величины попадут в интервал
. Найти вероятность того, что а) значения случайной величины попадут в интервал  , б) случайная величина
, б) случайная величина  отклонится по модулю от математического ожидания не более чем на
отклонится по модулю от математического ожидания не более чем на  .
. распределена по нормальному закону, то вероятность, что значения этой случайной величины попадут в интервал
распределена по нормальному закону, то вероятность, что значения этой случайной величины попадут в интервал  , находится по формуле:
, находится по формуле: ,
, - математическое ожидание,
- математическое ожидание, 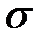 - среднеквадратическое отклонение, а значения функции
- среднеквадратическое отклонение, а значения функции  находим по таблице 4.
находим по таблице 4.
 отклонится по модулю от математического ожидания
отклонится по модулю от математического ожидания 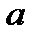 не более чем на
не более чем на  находится по формуле:
находится по формуле:
 .
. , б)
, б)  .
.









 .
. 25. В круг случайным образом брошена точка так, что любое её положение в круге равновозможно. Найти вероятность того, что она окажется внутри: А - вписанного в круг квадрата; В - вписанного в круг равностороннего треугольника.
25. В круг случайным образом брошена точка так, что любое её положение в круге равновозможно. Найти вероятность того, что она окажется внутри: А - вписанного в круг квадрата; В - вписанного в круг равностороннего треугольника. ;
; 


