Квазиполным графом Q(q) называют граф Q, для минимальной раскраски которого необходимо q-красок, а при раскраске любого собственного частичного графа Q`ÌÌQ достаточно q`-красок, где q`<q
Число красок при этом называется квазиплотностью и определяется выражением:
q(G)=max qi(Qi), QiÌ G
Порядок квазиполного графа это число k(Q) = q(Q)-p(Q), где p(Q) – плотность графа.
Если хроматическое число меняется при удалении одной вершины, то этот граф критический.
Плотность графа – максимальная мощность полного подграфа. (Полный граф – такой граф, в котором все вершины смежны)
Основное свойство квазиполных графов – при удалении хотя бы одного ребра хроматическое число уменьшается на единицу.
Повышение порядка квазиполного графа:
1.Для построения Q(p,k) необходимо построить Q(p,k-1)
2.Для всех ViÎV(Q(p,k-1) создать вершину Vi’ такую, что "Vi’: О(Vi’) = О(Vi)
3.Создать вершину Vо; О(Vо)={ Vi’}, для всех i
Вершины Vi’ называются замещающими, Vо – замыкающая вершина.
Теорема: Сумма квазиполных графов является квазиполным графом.
Для квазиполных графов справедливо свойство включаемости:
Q(p,k)ÌQ(p+1,k+1)
Например:Q(2,0)ÌQ(2,1)ÌQ(2,2)ÌQ(3,2)
Гиперкуб
Гиперкуб – это математическая модель дискретного пространства.
Гиперкуб – это граф, носитель которого соответствует точкам математического пространства, и две вершины смежны в том случае, если соответствующие им точки пространства имеют общую границу, т.е. расстояние по Хэммингу между координатами этих точек =1.
Иначе говоря, гиперкуб – это математическая модель дискретного пространства размерности n, представляющая собой граф, носителем которого являются вершины, каждая из которых соответствует точке пространства, и два вершины соединяются ребром, если между точками, соответствующими этим вершинам, есть различие и только в одном разряде. Мощность его носителя равна 2n, мощность сигнатуры равна n*2n-1.
Для булевого пространства, т.е. пространства, в котором каждая координата может принимать значение 0 или 1, расстояние по Хэммингу равно количеству различных координат (различных разрядов в координатах).
Свойства гиперкуба, вытекающие из ярусной упорядоченности вершин гиперкуба:
Если вершины в гиперкубе упорядочены по ярусам таким образом, что в одном ярусе сгруппированы вершины, в кодах которых одинаковое количество нулей или единиц, то:
1)количество ярусов = n+1, где n – размерность гиперкуба.
2) количество вершин в каждом ярусе  , n – размерность, k - значность
, n – размерность, k - значность
3) вершины в ярусе смежны только с вершинами из верхнего яруса или из нижнего яруса.
+
4) степень вершины гиперкуба размерности n равна n.
5) размерность n содержит 2nвершин
3) H=2 для любого гиперкуба с k=2 (если значность k гиперкуба равна 2, то хроматическое число H равно 2.
Гиперкубы находят применение в теории кодирования при передаче данных и при проектировании автоматов.
Вложение графа в гиперкуб
Большой практический интерес представляет проблема вложения графов в другие графы, имеющие специальные структурные свойства. Важным классом таких графов является класс n-мерных кубов. Они находят применение в теории кодирования при передаче данных и при проектировании автоматов. Обозначим n-мерный куб через Hn. Мощность его носителя равна 2n, мощность сигнатуры – n*2n-1. Множество вершин n-куба вместе с введенной таким образом метрикой, является метрическим пространством, которое назовем булевым пространством. Граф  называется вложимым в булево пространство Нn<VH,UH> или кубируемым, если существует соответствие ϕ между вершинами графа G и гиперкуба Hnтакое, что если (
называется вложимым в булево пространство Нn<VH,UH> или кубируемым, если существует соответствие ϕ между вершинами графа G и гиперкуба Hnтакое, что если ( .Так как n-куб является двудольным графом, то в соответствии с теоремой Кёнига все его простые циклы четны, и поэтому любой граф, который содержит подграф, являющийся нечетным циклом, некубируем. Следовательно циклы нечетной длины и граф Кёнига К2,3
.Так как n-куб является двудольным графом, то в соответствии с теоремой Кёнига все его простые циклы четны, и поэтому любой граф, который содержит подграф, являющийся нечетным циклом, некубируем. Следовательно циклы нечетной длины и граф Кёнига К2,3  являются запрещенными фигурами вложения графа в булево пространство. Под запрещенной фигурой в данном случае понимаем критически невложимый граф, т.е. некубируемый граф, у которого все частичные графы кубируемые.
являются запрещенными фигурами вложения графа в булево пространство. Под запрещенной фигурой в данном случае понимаем критически невложимый граф, т.е. некубируемый граф, у которого все частичные графы кубируемые. 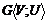 ;
;  называется изоморфным если существует такое взаимно однозначное соответствие между вершинами V и V’, что вершины Va и Vв соединены дугой (Va,Vв) в одном из графов в том и только в том случае когда соответствующие им вершины V’a и V’в соединены дугой (V’a,V’в) в другом графе.
называется изоморфным если существует такое взаимно однозначное соответствие между вершинами V и V’, что вершины Va и Vв соединены дугой (Va,Vв) в одном из графов в том и только в том случае когда соответствующие им вершины V’a и V’в соединены дугой (V’a,V’в) в другом графе.  граф G изоморфен графу G’. Два графа гомеоморфные если они изоморфны с точностью степени два. Вложить граф в гиперкуб это значит установить изоморфизм между графом и гиперкубом. Гиперкубом – называется граф каждая вершина которого соответствует области пространства, и две вершины соединены ребром если они соответствуют соседним областям имеющих общую границу. Размерность пространства- размерность гиперкуба, n-значность логики.
граф G изоморфен графу G’. Два графа гомеоморфные если они изоморфны с точностью степени два. Вложить граф в гиперкуб это значит установить изоморфизм между графом и гиперкубом. Гиперкубом – называется граф каждая вершина которого соответствует области пространства, и две вершины соединены ребром если они соответствуют соседним областям имеющих общую границу. Размерность пространства- размерность гиперкуба, n-значность логики.
Алгоритм вложения графа в гиперкуб.
1)устраняем запрещенные фигуры – структура в графе мешающая решению поставленной задачи-циклы нечетной длины, запрещенные фигуры при вложении графа в гиперкуб. Удаление запрещенных фигур осуществляется путем навешивания дополнительных вершин на соответствующие ребра.
2)Устанавливаем размерность а)maxS(V1); в) ] log2|V| [; из а и в выбираем мах- это и будет размерность гиперкуба: n = max(maxS(V1), ] log2|V| [)
3)Ярусно упорядочиваем граф начиная с вершины с мах
степенью устанавливаем изоморфизм между графом и гиперкубом размерности n. При необходимости размерность куба может быть увеличена.
Если при установке изоморфизма невозможно установить соответствие между какой-либо вершиной графа и вершиной гиперкуба из-за топологических свойств, можно удалить какое-либо ребро графа путем навешивания 2-х дополнительных вершин на это ребро.
Планарный граф. Вложение графа в плоскость
Планарный граф — граф, который может быть изображен на плоскости без пересечения ребер. Граф укладывается на некоторой поверхности, если его можно на ней нарисовать без пересечения ребер. Уложенный граф называется геометрическим, его вершины — это точки плоскости, а ребра — линии на ней. Области, на которые граф разбивает поверхность, называются гранями. Плоский граф — граф, уложенный на плоскость. Граф называется планарным, если он изоморфен некоторому плоскому графу
*я незнаю нужно ли это или нет
Топология исследует свойства графов, инвариантные относительно гомеоморфных преобразований. Эти свойства определяются топологическими инвариантами. Два графа гомеоморфны, если они изоморфны с точностью до вершин степени 2. Другими словами, два графа гомеоморфны, если они преобразуются до графов, изоморфных друг другу, заменой некоторых ребер цепями соответствующей длины. Род поверхности – это наибольшее число простых замкнутых кривых на поверхности, которые не разъединяют эту поверхность. Сфера и плоскость являются поверхностями нулевого рода, поскольку их разъединяет любая замкнутая прямая. Тор поверхность первого рода. Любая поверхность p-го рода эквивалентна сфере с p ручками.
Граф называется планарным, если он изображается на плоскости так, что его ребра пересекаются только в вершинах. Теорема: Граф планарен тогда и только тогда, когда он не содержит подграфа, гомеоморфного F5 или К3,3 или графов стягиваемых к F5 или к К3,3. Толщиной графа G называется наименьшее число планарных графов, объединение которых дает G. Толщина планарного графа равна 1. Нижняя оценка толщины t(G) графа  определяется неравенством
определяется неравенством  , где ] [ -целая часть, |V|=n, si- степень i –ой вершины. Чтобы определить, какие ребра необходимо удалить для преобразования графа в планарный, выделим все запрещенные фигуры и построим двумерную таблицу, каждая строка которой взаимно однозначно соответствует запрещенной фигуре Qi, a столбец – ребру Pi. тогда покрытие строк столбцами этой таблицы определит, какие ребра необходимо удалить, чтобы граф стал планарным. Минимальное покрытие будет соответствовать минимальному решению, так как удаление любого ребра выводит запрещенную фигуру из класса подграфов, гомеоморфных F5 или К3,3.
, где ] [ -целая часть, |V|=n, si- степень i –ой вершины. Чтобы определить, какие ребра необходимо удалить для преобразования графа в планарный, выделим все запрещенные фигуры и построим двумерную таблицу, каждая строка которой взаимно однозначно соответствует запрещенной фигуре Qi, a столбец – ребру Pi. тогда покрытие строк столбцами этой таблицы определит, какие ребра необходимо удалить, чтобы граф стал планарным. Минимальное покрытие будет соответствовать минимальному решению, так как удаление любого ребра выводит запрещенную фигуру из класса подграфов, гомеоморфных F5 или К3,3.



 , n – размерность, k - значность
, n – размерность, k - значность называется вложимым в булево пространство Нn<VH,UH> или кубируемым, если существует соответствие ϕ между вершинами графа G и гиперкуба Hnтакое, что если (
называется вложимым в булево пространство Нn<VH,UH> или кубируемым, если существует соответствие ϕ между вершинами графа G и гиперкуба Hnтакое, что если ( .Так как n-куб является двудольным графом, то в соответствии с теоремой Кёнига все его простые циклы четны, и поэтому любой граф, который содержит подграф, являющийся нечетным циклом, некубируем. Следовательно циклы нечетной длины и граф Кёнига К2,3
.Так как n-куб является двудольным графом, то в соответствии с теоремой Кёнига все его простые циклы четны, и поэтому любой граф, который содержит подграф, являющийся нечетным циклом, некубируем. Следовательно циклы нечетной длины и граф Кёнига К2,3  являются запрещенными фигурами вложения графа в булево пространство. Под запрещенной фигурой в данном случае понимаем критически невложимый граф, т.е. некубируемый граф, у которого все частичные графы кубируемые.
являются запрещенными фигурами вложения графа в булево пространство. Под запрещенной фигурой в данном случае понимаем критически невложимый граф, т.е. некубируемый граф, у которого все частичные графы кубируемые. 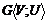 ;
;  называется изоморфным если существует такое взаимно однозначное соответствие между вершинами V и V’, что вершины Va и Vв соединены дугой (Va,Vв) в одном из графов в том и только в том случае когда соответствующие им вершины V’a и V’в соединены дугой (V’a,V’в) в другом графе.
называется изоморфным если существует такое взаимно однозначное соответствие между вершинами V и V’, что вершины Va и Vв соединены дугой (Va,Vв) в одном из графов в том и только в том случае когда соответствующие им вершины V’a и V’в соединены дугой (V’a,V’в) в другом графе.  граф G изоморфен графу G’. Два графа гомеоморфные если они изоморфны с точностью степени два. Вложить граф в гиперкуб это значит установить изоморфизм между графом и гиперкубом. Гиперкубом – называется граф каждая вершина которого соответствует области пространства, и две вершины соединены ребром если они соответствуют соседним областям имеющих общую границу. Размерность пространства- размерность гиперкуба, n-значность логики.
граф G изоморфен графу G’. Два графа гомеоморфные если они изоморфны с точностью степени два. Вложить граф в гиперкуб это значит установить изоморфизм между графом и гиперкубом. Гиперкубом – называется граф каждая вершина которого соответствует области пространства, и две вершины соединены ребром если они соответствуют соседним областям имеющих общую границу. Размерность пространства- размерность гиперкуба, n-значность логики. определяется неравенством
определяется неравенством  , где ] [ -целая часть, |V|=n, si- степень i –ой вершины. Чтобы определить, какие ребра необходимо удалить для преобразования графа в планарный, выделим все запрещенные фигуры и построим двумерную таблицу, каждая строка которой взаимно однозначно соответствует запрещенной фигуре Qi, a столбец – ребру Pi. тогда покрытие строк столбцами этой таблицы определит, какие ребра необходимо удалить, чтобы граф стал планарным. Минимальное покрытие будет соответствовать минимальному решению, так как удаление любого ребра выводит запрещенную фигуру из класса подграфов, гомеоморфных F5 или К3,3.
, где ] [ -целая часть, |V|=n, si- степень i –ой вершины. Чтобы определить, какие ребра необходимо удалить для преобразования графа в планарный, выделим все запрещенные фигуры и построим двумерную таблицу, каждая строка которой взаимно однозначно соответствует запрещенной фигуре Qi, a столбец – ребру Pi. тогда покрытие строк столбцами этой таблицы определит, какие ребра необходимо удалить, чтобы граф стал планарным. Минимальное покрытие будет соответствовать минимальному решению, так как удаление любого ребра выводит запрещенную фигуру из класса подграфов, гомеоморфных F5 или К3,3.


