

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Пример 10.1. Вычислить 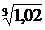
► Рассмотрим функцию y = 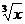 . Вычислим ее производную в точке x = 1: y`(1) = 1/3.
. Вычислим ее производную в точке x = 1: y`(1) = 1/3.
По формуле малых приращений имеем (Dx = 0,02):
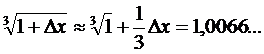 ◄
◄
Пример 10.2. Вычислить sin 290
► Рассмотрим функцию y = sinx. Ее производная в точке x = p/6 = 300 равна 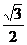 . Тогда по формуле малых приращений получим (Dx =-p/180)
. Тогда по формуле малых приращений получим (Dx =-p/180)
sin29 = sin(p/6-p/180)» sinp/6 – 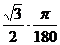 = 1/2(1 –
= 1/2(1 – 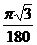 ) = 0,484 ….◄
) = 0,484 ….◄
1) sin60015' 2) cos60015' 3) tg60015' 4) ctg60015'
5) 20.013' 6) 50.012 7) 90.501 8) 2.013
9) 5.012 10) 91/3 11) 801/4 12) 1001/8
13) 10001/11 14) lg11 15) arctg1.05 16) sin46
17) cos 44 18) (7.01)3 19) (7.01)4 20) (7.01)7
21) arcsin0.99 22) arccos0.09 23) cos29 24) tg44
25) ctg46 26) arctg0.99 27) 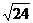 28)
28) 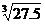
29) 160.503 30) sin14.5cos14.5
11. Найти уравнение касательной к графику функции y=f(x) в точке с абсциссой x0. Сколько общих точек имеет график данной функции с искомой касательной
Пример 11.1. y = x2/2 x0 = 0
► y`=x по формуле уравнения касательной получим y = 0 + 0 = 0 Þ y = 0.
Найдем точки пересечения графика функции и касательной
x2/2 = 0 Þ x = 0 единственная точка совпадения графика функции с касательной – точка (0,0).◄
Пример 11.2. y = sinx, x0 = p/2.
►y`=cosx, y(x0)=1, y`(x0) = 0. Запишем уравнение касательной y = 1. Таким образом в точках пересечения графика функции и касательной получаем уравнение
sinx = 1 Þ x = p/2+2pk, kÎZ.
То есть, график функции имеет бесконечное число общих точек со своей касательной. Легче было решить эту задачу графически, так как, очевидно, что прямая y =1 будет касаться графика y = sinx во всех его «верхних» точках, а таких точек на всей числовой оси бесконечно много. ◄
1) y = sin3x +2, при x0 = 0. 2) y = cos5px +6, при x0 = 1
3) y = sin5(x - 2), при x0 = 2 4) y = cos5px +8, при x0 = 1
5) y = tgpx +2, при x0 = 1 6) y= ctg(px/2) +2, при x0 =1
7) y = arctg2x +4, при x0 = 1 8) y= arcctg3x +6, при x0 = 1/6
9) y = ax2+bx +c, при x0 = –b/(2a) 10) y = ax+b, при x0 = –b/(2a)
11) y = 1/x2, при x0 = –1 12) y = x3+bx +c, при x0 = 0
13) y = (x+1)/(x-1), при x0 = –1/2 14) y = x2/(1+x), при x0 = –1
15) y = (x+1)/(3-x)1/3, при x0 = 2 16) y = sin4x – 1, при x0 = p/8
|
|
17) y = sin2(x - 1), при x0 = 3 18) y = cos2x +3, при x0 = 0
19) y = tg4px +2, при x0 = 1 20) y= ctg(3px/2) +2, при x0 = 1
21) y = arctgx/2 +1, при, x0 = 1 22) y= arcctg3x/4 +6, при x0 = 1/8
23) y = 3/2x2, при x0 = 7/2 24) y = x2+5x +23/24, при x0 = 5/4
25) y = (2x+3)/(7x-15), при x0 = 7/5 26) y = x4/2(4+2x), при x0 = 1/2
27) y = tg46x –1/e, при x0 = 2e 28) y = ctg(3x/8) -5, при x0 = 1
29) y = (3x+9)/(6-2x)1/5, при x0 =–2/3 30) y = sin4x/11 – 2, при x0 = 11p/8
12. Найти k-ю производную от функции y = f(x)
Пример 12.1. y=ax-m, k=3
► Последовательно дифференцируя, имеем:
y` = –max-m-1;
y`` = –ma(x-m-1)` = am(m+1)x-m-2;
y``` = am(m+1)(x-m-2)`= –am(m+1)(m+2)x-m-3◄
Пример 12.2. y= 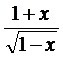 , k = 100.
, k = 100.
► Преобразуем данную функцию к удобному для дифференцирования виду
y = 2(1-x)-1/2-(1-x)1/2
После 100-кратного дифференцирования получаем:
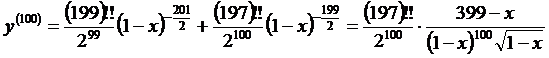 ◄
◄
1) k = 38, y = xex 2) k = 45, y = ex2
3) k = 30, y = sinx +ex 4) k = 39, y = cosx+ex
5) k = 68, y = cos2x +ex 6) k = 100, y = ln2x +ex
7) k = 50, y = 2x+ex 8) k = 618, y = (3x)121+ex
9) k = 63, y = 1+ex 10) k = 87, y = +ex+1/(x+1)
11) k = 88, y = 1/(1-x2)+ex 12) k = 98, y = 1/x+ex
13) k = 78, y = 756x8+56x6+ex 14) k = 6, y = 1+cos(x)ex
15) k = 5, y = +sin(x)ex 16) k = 6, y = x(2x–1)2(x+3)3
17) k = 3, y =  18) k = 100, y =
18) k = 100, y = 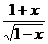
19) k = 20, y = x2e2x 20) k = 10, y = 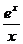
21) k = 6, y = sin2xlnx 22) k =100, y = xshx
23) k = 10, y = sinxsin2xsin3x 24) k = 50, y = x2sin2x
25) k = 5, y = xlnx 26) k = 5, y = 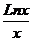
27) k = 8, y = 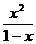 28) k = 10, y =
28) k = 10, y = 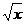
29) k = 6, y = cosxchx 30) k = 10, y = (2x–1)23x32x
13. С помощью правила ЛОПИТАЛЯ найти предел функции y =f(x) при x 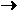 x0.
x0.
Пример 13.1. 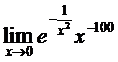
►Непосредственное применение правила Лопиталя не эффективно, поэтому, произведя замену 1/x2 = y и применив правило Лопиталя к полученному выражению получим
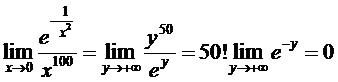 ◄
◄
Пример 13.2. 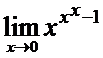
► Здесь имеется неопределенность вида 00, поэтому предварительно воспользуемся представлением  (u>0, v>0), а также соотношением
(u>0, v>0), а также соотношением 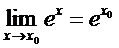 , вытекающим из непрерывности функции ex.
, вытекающим из непрерывности функции ex.
После очевидных преобразований и применения правила Лопиталя получаем
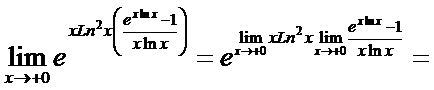
 ◄
◄
1) x0 = +0 y = xx. 2) x0 = a y = (ax–xa)/(x–a)
3) x0 = п/2 y = tg(3x)/tgx. 4) x0 = 0 y = (tg(x)–x)/(x–sinx).
5) x0 = 0 y = sinax/sinbx. 6) x0 =1 y = x1/(1–x).
7) x0 = +0 y = (ln(1/x))x. 8) x0 = 0 y = xalnx (a>0).
9) x0 = 0 y = ((1+x)1/x-e)/x. 10) x0 = 0 y = (1-cos(x2))/(x2sin(x2)).
11) x0 =¥ y = lnx/xa(a>0). 12) x0 = 0 y = sinax/tgbx.
13) x0=0 y = ln(sin(ax))/ln(sin(bx)). 14) x0 = 0 y = ln(cos(bx))/ln(cos(ax))
15) x0 = 0 y = (cos(sinx))-cosx)/x4. 16) x0 = 0 y = 
17) x0=0 y= 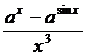 18) x0 = 1 – 0 y = lnx×ln(1-x)
18) x0 = 1 – 0 y = lnx×ln(1-x)
19) x0=0 y= 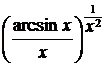 20) x0 ® +¥ y = (thx)x
20) x0 ® +¥ y = (thx)x
21) x0 = 0 y = 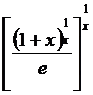 22) x0 = 0 y =
22) x0 = 0 y = 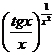
23) x0 = 0 y =  24) x0 = 0 y =
24) x0 = 0 y = 
25) x0 = 0 y =  26) x0 = 0 y =
26) x0 = 0 y = 
|
|
27) x0 = 1 y = 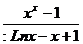 28) x0 = 0 y =
28) x0 = 0 y = 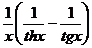
29) x0 = +0 y = 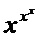 -1 30) x0 = p/4 y = (tgx)tg2x
-1 30) x0 = p/4 y = (tgx)tg2x
14.Найти второй дифференциал функции y = f(x) определяемой уравнением
Пример 14.1. y=lnx
► Находим последовательно
dy = – dx/x;
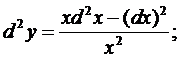
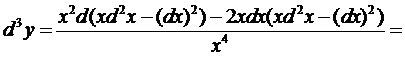

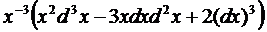 ◄
◄
Пример 14.2. y = f(x), где x – функция от некоторой независимой переменной.
► Исходя из определения дифференциалов высших порядков, имеем:
dy = f`dx; d2y = d(f`dx) = f``(dx)2 + f`d2x;
d3y = d(f``(dx)2 + f`d2x) =
f```(dx)3 + 2f``dxd2x + f``dxd2x + f`d3x = f```(dx)3 + 3d2xdxf`` + f`d3x.◄
1) sin(x + y) =y 2) tg(x + y) = y
3) exy + x + y = 0 4) log3(x + y) = x + y
5) log4(x2 + y) = 1-y 6) arccos(3x4 + y2) = y
7) (1 + x2 + y2)1/3= x-y2 8) arctg(x4 + 3y) = x + y6
9) arcctg(x5 + 2y) = x + y3 10) 2xy + y= xy + x
11) 31/(x + y)= xy 12) xy= x + y
13) yx = x2 + y3 14) (x + y)(x + y) = x4 + y7
15) logxy = x+y2 16) sin2(x + y) = 3y
17) logxy = (x+y)2 18) 3x + y + 2x + 5y = 0
19) y3 = x3 + 3y 20) arctg(x – y) = x + y
21) x2y = xx 22) ln(2x + 3y) = x – 2y2
23)  = x2-y2 24) cos(xy) = sin(x + y)
= x2-y2 24) cos(xy) = sin(x + y)
25) tg(cosxy) = lnx3 26) (x + y)3 = xy
27) log3xx + y = y2 28) 2x + y = xy
29) lncos(x3 + y) = x + y5 30) x3x + y3 = 2xy
15. Построить с помощью элементарных преобразований графики функций
1. 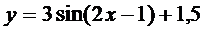
| 2. 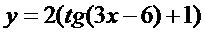
|
3. 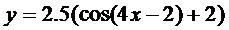
| 4. 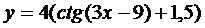
|
5. 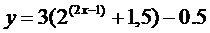
| 6. 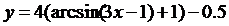
|
7. 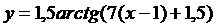
| 8. 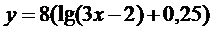
|
9. 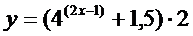
| 10. 
|
11. 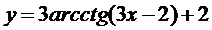
| 12. 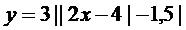
|
13. 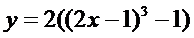
| 14. 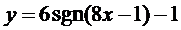
|
15. 
| 16. 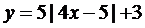
|
17. 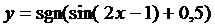
| 18. 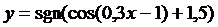
|
19. 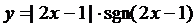
| 20. 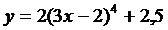
|
21. 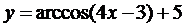
| 22. 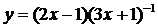
|
23. 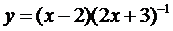
| 24. 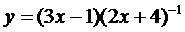
|
25. 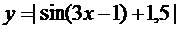
| 26. 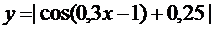
|
27. 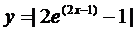
| 28. 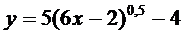
|
29. 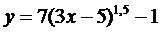
| 30. 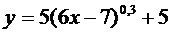
|
|
|
|

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!