Полным приращением функции  в точке
в точке  соответствующим приращениям аргументов
соответствующим приращениям аргументов  называется разность
называется разность
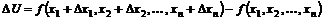
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  если всюду в некоторой окрестности этой точки полное приращение функции может быть представлено в виде
если всюду в некоторой окрестности этой точки полное приращение функции может быть представлено в виде

где  – числа, не зависящие от
– числа, не зависящие от  .
.
Дифференциалом  1–ого порядка функции
1–ого порядка функции  в точке
в точке  называется главная часть полного приращения этой функции в рассматриваемой точке, линейная относительно
называется главная часть полного приращения этой функции в рассматриваемой точке, линейная относительно  , т.е.
, т.е.
 .
.
Дифференциалы независимых переменных по определению принимаются равными их приращениям:
 .
.
Для дифференциала функции  справедлива формула
справедлива формула
 .
.
Функции нескольких переменных подчиняются обычным правилам дифференцирования:
 ;
;
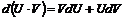 ;
;
 ;
;
Дифференциалы высших порядков функции двух переменных  имеют вид:
имеют вид:
 ;
;
 .
.
Аналогично,  ,
,  .
.
Пример.
Найти полное приращение и дифференциал функции 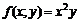 в точке
в точке 
Решение.


 .
.

Основное свойство первого дифференциала
При достаточно малых приращениях аргумента для дифференцируемой функции  имеет место приближеннее равенство
имеет место приближеннее равенство
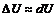 .
.
Или



Пример.
Вычислить приближенно  .
.
Решение.
Рассмотрим функцию:  .
.
 ;
;
 ;
;
 ;
;
 ;
;  ;
;

Тогда  .
.
Задачи.
11.27. Найти полное приращение и дифференциал функции  если x изменяется от 2 до 2,1, а y от 1 до 1,2.
если x изменяется от 2 до 2,1, а y от 1 до 1,2.
Найти дифференциалы функций:
11.28.  ; 11.29.
; 11.29.  ;
;
11.30.  ; 11.31.
; 11.31. 
Вычислить приближенно:
11.32.  ;
;
11.33.  ;
;
11.34.  ;
;
11.35.  ;
;
11.36.  ;
;
11.37.  .
.
Формула Тейлора для функции двух переменных
Если функция  дифференцируема (
дифференцируема ( ) раз в некоторой окрестности точки
) раз в некоторой окрестности точки  , то для любой точки
, то для любой точки 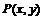 из этой окрестности справедлива формула Тейлора:
из этой окрестности справедлива формула Тейлора:


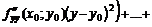
 , где
, где  .
.
Или
 .
.
В частном случае, при  , получим формулу Маклорена:
, получим формулу Маклорена:


 .
.
Пример.
Функцию  разложить по формуле Тейлора в окрестности точки
разложить по формуле Тейлора в окрестности точки 
Решение.
Имеем,  Вычислим последовательно частные производные данной функции и их значения в точке
Вычислим последовательно частные производные данной функции и их значения в точке 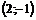 :
:

 ;
;

 ;
;
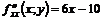 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
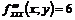 ;
;  .
.
Все последующие производные тождественно равны 0.
В результате, получим

 .
.
Задачи.
11.38. Функцию  разложить по формуле Тейлора в окрестности точки
разложить по формуле Тейлора в окрестности точки 
11.39. Функцию  разложить по формуле Тейлора в окрестности точки
разложить по формуле Тейлора в окрестности точки 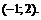
11.40. Разложить по формуле Маклорена до членов 4–го порядка включительно функцию 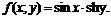
11.41. Разложить по формуле Тейлора в окрестности точки (1,1) до членов 3–го порядка включительно функцию  .
.
11.42. Разложить по формуле Маклорена до членов 2–го порядка включительно функцию  .
.
Экстремум функции двух переменных
Функция  имеет максимум (минимум) в точке
имеет максимум (минимум) в точке  , если существует такая окрестность точки
, если существует такая окрестность точки  для всех точек P которой, отличных от точки
для всех точек P которой, отличных от точки  выполняется неравенство
выполняется неравенство  (соответственно
(соответственно  ).
).
Максимум и минимум функции называется ее экстремумом.
Необходимое условие экстремума
Если дифференцируемая функция  достигает экстремума в точке
достигает экстремума в точке  то в этой точке
то в этой точке
 и
и  .
.
Точки, в которых выполняются необходимые условия экстремума, называются стационарными точками функции  .
.



 в точке
в точке  соответствующим приращениям аргументов
соответствующим приращениям аргументов  называется разность
называется разность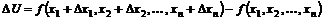
 называется дифференцируемой в точке
называется дифференцируемой в точке  если всюду в некоторой окрестности этой точки полное приращение функции может быть представлено в виде
если всюду в некоторой окрестности этой точки полное приращение функции может быть представлено в виде
 – числа, не зависящие от
– числа, не зависящие от  .
. 1–ого порядка функции
1–ого порядка функции  называется главная часть полного приращения этой функции в рассматриваемой точке, линейная относительно
называется главная часть полного приращения этой функции в рассматриваемой точке, линейная относительно  .
. .
. справедлива формула
справедлива формула .
. ;
;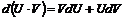 ;
; ;
; имеют вид:
имеют вид: ;
; .
. ,
,  .
.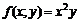 в точке
в точке 


 .
.
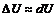 .
.


 .
. .
. ;
; ;
; ;
; ;
;  ;
;
 .
. если x изменяется от 2 до 2,1, а y от 1 до 1,2.
если x изменяется от 2 до 2,1, а y от 1 до 1,2. ; 11.29.
; 11.29.  ;
; ; 11.31.
; 11.31. 
 ;
; ;
; ;
; ;
; ;
; .
. дифференцируема (
дифференцируема ( ) раз в некоторой окрестности точки
) раз в некоторой окрестности точки  , то для любой точки
, то для любой точки 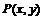 из этой окрестности справедлива формула Тейлора:
из этой окрестности справедлива формула Тейлора:

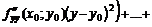
 , где
, где  .
. .
. , получим формулу Маклорена:
, получим формулу Маклорена:

 .
. разложить по формуле Тейлора в окрестности точки
разложить по формуле Тейлора в окрестности точки 
 Вычислим последовательно частные производные данной функции и их значения в точке
Вычислим последовательно частные производные данной функции и их значения в точке 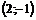 :
:
 ;
;
 ;
;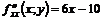 ;
;  ;
; ;
;  ;
; ;
;  ;
;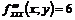 ;
;  .
.
 .
. разложить по формуле Тейлора в окрестности точки
разложить по формуле Тейлора в окрестности точки 
 разложить по формуле Тейлора в окрестности точки
разложить по формуле Тейлора в окрестности точки 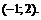
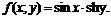
 .
. .
. имеет максимум (минимум) в точке
имеет максимум (минимум) в точке  для всех точек P которой, отличных от точки
для всех точек P которой, отличных от точки  (соответственно
(соответственно  ).
). достигает экстремума в точке
достигает экстремума в точке  и
и  .
.


