Пусть в уравнении
y ¢ = f (x, y)
функция f (x, y) может быть разложена на множители, каждый из которых зависит только от одной переменной х или у:
f (x, y) = f 1(x) f 2(у)
или в уравнении
M (x, y) dx + N (x, y) dy = 0
коэффициенты при dx и dy представляются в виде M (x, y) = M 1(x) M 2(у), N (x, y) = N 1(x) N 2(у). Путем деления соответственно на f 2(у) и на
N 1(x) M 2(у) эти уравнения приводятся соответственно к виду
f 1(x) dx = 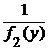 dy,
dy, 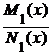 dx = –
dx = – 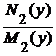 dy.
dy.
Интегрируя левые части этих уравнений по х, а правые по у, приходим в каждом из них к общему интегралу исходного дифференциального уравнения.
Пример 1. Решить задачу Коши 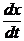 = k (a – x) (b – x), x (0) = 0,
= k (a – x) (b – x), x (0) = 0,
полученную в примере составления дифференциального уравнения в задании с практической задачей.
• Исходное уравнение - это уравнение с разделяющимися переменными:
 = k dt.
= k dt.
Преобразуем полученное уравнение к виду
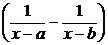
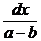 = k dt.
= k dt.
Интегрируем правую и левую части и получаем:
ln | x – a | – ln | x – b | = k (a – b) t + ln | C | => 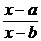 = C e k (a – b) t .
= C e k (a – b) t .
Из начальных условий (x (0) = 0) имеем: С = 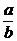 , поэтому
, поэтому
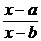 =
= 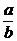 e k (a – b) t ,
e k (a – b) t ,
откуда x (t) = a b  .
.
Пример 2. Решить уравнение 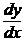 =
= 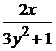 .
.
• Разделяем переменные (3 y 2 + 1) dy = 2 x dx. Интегрируем:
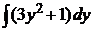 =
= 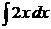
и получаем общий интеграл уравнения у 3 + у – х 2 = С.
Однородные уравнения
Дифференциальное уравнение 1-го порядка называется однородным,
если его можно привести к виду
y ¢ = f 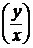 (5)
(5)
или к виду
M (x, y) dx + N (x, y) dy = 0, (6)
где M (x, y) и N (x, y) – однородные функции одного порядка, т.е. существует такое k  Z, что M (t x, t y) = t k M (x, y) и N (t x, t y) = t k N (x, y).
Z, что M (t x, t y) = t k M (x, y) и N (t x, t y) = t k N (x, y).
С помощью подстановки 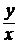 = u (x) (y = xu => y ¢ = u + x u ¢) однородные уравнения (5) и (6) преобразуются в уравнения с разделяющимися переменными.
= u (x) (y = xu => y ¢ = u + x u ¢) однородные уравнения (5) и (6) преобразуются в уравнения с разделяющимися переменными.
Пример 3. Решить уравнение y ¢ = 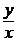 + cos
+ cos 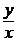 .
.
• Положим 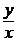 = u или y = xu. Тогда y ¢ = u + x u ¢, что после подстановки в исходное уравнение дает уравнение с разделяющимися переменными
= u или y = xu. Тогда y ¢ = u + x u ¢, что после подстановки в исходное уравнение дает уравнение с разделяющимися переменными
u + x u ¢ = u + cos u или x 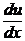 = cos u.
= cos u.
Разделяем переменные
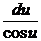 =
= 
и интегрируем
tg  = Cx.
= Cx.
Получаем общее решение
u = 2 arctg Cx – 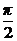 + 2 πn, n
+ 2 πn, n  Z.
Z.
Возвращаясь к функции у, находим:
у = х  , n
, n  Z.
Z.
При делении на cos u были потеряны решения у = х  , k
, k  Z.
Z.
Добавляя их к полученному семейству решений, окончательно находим
у = х  , n
, n  Z; у = х
Z; у = х  , k
, k  Z.
Z.
Линейные уравнения
Линейным дифференциальным уравнением 1-го порядка называется
уравнение вида
y ¢ + p (x) y = q (x), (7)
где p (x) и q (x) – заданные и непрерывные на некотором промежутке функции.
Существует несколько методов интегрирования уравнения (7). Рассмотрим самый распространенный из них – метод Бернулли, называемый «методом u на v». Суть метода в том, что решение этого уравнения ищется в виде произведения
у = u v, (8)
где u = u (x), v = v (x) – неизвестные функции х, причем одна из этих функций произвольна (но не равна тождественно нулю).
Подставляя решение у = u v и его производную у ¢ = u ¢ v + u v ¢ в уравнение (7), получим
u ¢ v + u v ¢ + p (x) u v = q (x) или u ¢ v + u (v ¢ + p (x) v) = q (x). (9)
Пользуясь произвольностью в выборе функции v (x), выберем ее так, чтобы выражение в скобках стало равным нулю
v ¢ + p (x) v = 0. (10)
Это уравнение с разделяющимися переменными. Решив его и подставив выражение для v в (9), получим следующее уравнение относительно u
u ¢ v = q (x). (11)
Решаем это уравнение, находим u = u (x, C). Таким образом, общее решение линейного уравнения (7) у = u (x, C) v.
Пример 4. Найти частное решение дифференциального
уравнения (решить задачу Коши) у ¢ = 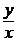 –
– 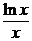 с начальными условиями у (1) = 1.
с начальными условиями у (1) = 1.
• Это линейное уравнение вида у ¢ + p (x) y = q (x), в котором p (x) = –  , q (x) = –
, q (x) = – 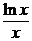 . Общее решение ищем в виде y = uv. Тогда y = u ¢ v + uv ¢. Имеем:
. Общее решение ищем в виде y = uv. Тогда y = u ¢ v + uv ¢. Имеем:
u ¢ v + uv ¢ –  = –
= – 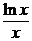 => u ¢ v + u
=> u ¢ v + u 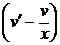 = –
= – 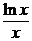 .
.
Подберем функцию v так, чтобы v ¢ –  = 0; тогда u ¢ v = –
= 0; тогда u ¢ v = – 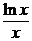 . Интегрируя первое из этих уравнений, получим:
. Интегрируя первое из этих уравнений, получим:
v ¢ –  = 0 =>
= 0 =>  =
=  =>
=> 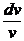 =
=  => ln | v | = ln | x | => v = х.
=> ln | v | = ln | x | => v = х.
Подставив полученное выражение для v во второе уравнение, получим:
u ¢ х = – 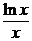 => du = –
=> du = –  dx.
dx.
Интегрируем обе части данного уравнения:  = –
= –  dx.
dx.
Второй интеграл берем по частям:
–  dx =
dx =  =
=  –
–  =
=  +
+  + C.
+ C.
Таким образом, u =  +
+  + C, а общее решение исходного уравнения
+ C, а общее решение исходного уравнения
y = uv = x  = ln x + 1 + Cx.
= ln x + 1 + Cx.
Подставим в это общее решение начальное условие:
1 = ln 1 + 1 + C ∙ 1 = 0 + 1 + C = 1 + C.
Отсюда получаем, что С = 0.
Таким образом, искомое частное решение имеет вид y = ln x + 1.
Уравнение Бернулли
Уравнением Бернулли называется дифференциальное уравнение 1-го порядка вида
y ¢ + p (x) y = q (x) yn, (12)
где n ≠ 0, n ≠ 1 (при n = 0 уравнение (12) является линейным, а при n = 1 – уравнением с разделяющимися переменными). Проинтегрировать уравнение Бернулли можно так же, как и линейное уравнение с помощью подстановки у = u v.
Пример 5. Решить дифференциальное уравнение у ¢ = 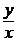 +
+  .
.
• Это уравнение Бернулли. Полагая у = u v, приведем исходное уравнение к виду u ¢ v + u  =
=  .
.
Решаем первое уравнение v ¢ –  = 0:
= 0:
v ¢ –  = 0 =>
= 0 =>  =
=  =>
=> 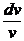 =
=  => ln | v | = ln | x | => v = х.
=> ln | v | = ln | x | => v = х.
Второе уравнение примет вид u ¢ х =  или u ¢ =
или u ¢ = 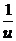 .
.
Решаем его: u ¢ = 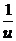 => u du = dx => u 2 = 2 x + C => u =
=> u du = dx => u 2 = 2 x + C => u =  . Перемножая u и v, получим общее решение исходного уравнения
. Перемножая u и v, получим общее решение исходного уравнения
у = х  .
.



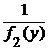 dy,
dy, 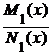 dx = –
dx = – 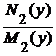 dy.
dy.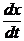 = k (a – x) (b – x), x (0) = 0,
= k (a – x) (b – x), x (0) = 0, = k dt.
= k dt.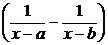
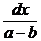 = k dt.
= k dt.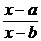 = C e k (a – b) t .
= C e k (a – b) t .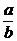 , поэтому
, поэтому .
.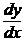 =
= 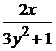 .
.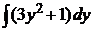 =
= 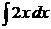
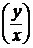 (5)
(5) Z, что M (t x, t y) = t k M (x, y) и N (t x, t y) = t k N (x, y).
Z, что M (t x, t y) = t k M (x, y) и N (t x, t y) = t k N (x, y).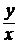 = u (x) (y = xu => y ¢ = u + x u ¢) однородные уравнения (5) и (6) преобразуются в уравнения с разделяющимися переменными.
= u (x) (y = xu => y ¢ = u + x u ¢) однородные уравнения (5) и (6) преобразуются в уравнения с разделяющимися переменными.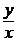 + cos
+ cos 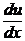 = cos u.
= cos u.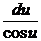 =
= 
 = Cx.
= Cx.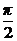 + 2 πn, n
+ 2 πn, n  , n
, n  , k
, k  , n
, n 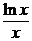 с начальными условиями у (1) = 1.
с начальными условиями у (1) = 1. , q (x) = –
, q (x) = –  = –
= – 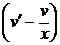 = –
= –  = 0; тогда u ¢ v = –
= 0; тогда u ¢ v = –  =
= 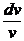 =
=  dx.
dx. = –
= –  dx.
dx. =
=  –
–  =
=  + C.
+ C. = ln x + 1 + Cx.
= ln x + 1 + Cx. .
. =
=  .
. или u ¢ =
или u ¢ = 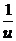 .
. . Перемножая u и v, получим общее решение исходного уравнения
. Перемножая u и v, получим общее решение исходного уравнения


