Задача. Имеется таблица значений некоторой функции:
| x
| f(x)
| x
| f(x)
|
| 0,41
| 2,63
| 2,67
| 4,87
|
| 1,55
| 3,75
| 3,84
| 5,03
|
Требуется получить значение этой функции в точке X=1,91.
Решение осуществляем с учетом формулы (20):

Результат:

f (1,91) ≈4,15
Метод наименьших квадратов. Применяется при обработке экспериментально полученных зависимостей, когда есть ряд значений параметра (хi) и соответствующий ему ряд значений неизвестной функции (yi). Лучшим аналитическим представлением этой зависимости будет функция φ(х), выбранная таким образом, чтобы сумма квадратов отклонений экспериментальных значений yi от φ(х), была минимальной, т. е.

Пусть дан ряд значений независимого аргумента Х (диапазон А1:А15) и соответствующих ему значений зависимого аргумента Y (функции) в диапазоне В1:В15.
| | А
| В
| С
| D
| E
| F
|
|
| Xi
| Yi
| Xi
| Yi
| m
| n
|
|
|
| 0,5
|
| 23,00
| | |
|
|
| 3,3
|
| 17,00
| | |
|
|
| 1,98
|
| 19,9
| | |
|
|
|
|
| 22,00
| | |
|
|
| 4,0
|
| 27,0
| | |
|
|
| 11,09
|
| 30,0
| | |
|
|
| 12,75
|
| 27,76
| | |
| | | |
|
| | |
(Результат: m=2,304393, n=-1,68314, a=1,208189; b=2,51309)
m=2,357964 n=-2,31171 a=1,264018 b=1,659488
Задача: Для заданного набора пар данных независимой переменной Хi и функции Yi определить наилучшее линейное приближение в виде прямой с уравнением y=mx+n и показательное приближение в виде линии с уравнением y=baх.
Решение:
1. Ячейка Е1 – текущая. Левой кнопкой мыши изменить формулу в строке формул (щелкнуть по кнопке с символом «=»). Раскрыть список в левом краю строки формул и выбрать Другие функции.
2. В окне Мастера функции (МФ) выбрать категорию Ссылки и массивы, и функцию ИНДЕКС, ОК. В новом диалоговом окне выбрать первый вариант набора параметров, ОК (массив, номер строки, номер столбца).
3. Установить текстовый курсор в первое поле для ввода параметров (массив) и снова выбрать Другие функции в раскрывшемся списке в строке формул.
4. С помощью МФ выбрать функцию ЛИНЕЙН категории СТАТИСТИЧЕСКИЕ, ОК.
5. В качестве первого параметра функции ЛИНЕЙН (изв_знач_у) выбрать диапазон, содержащий значения функции(столбец В).
6. В качестве второго параметра функции ЛИНЕЙН (изв_знач_х) выбрать диапазон, содержащий значения независимой переменной (столбец А), ОК. На появившемся сообщении – ОК.
7. Поместить текстовый курсор в строке формул между двумя закрывающимися скобками и нажать «;1». Это третий недостающий параметр функции ИНДЕКС. Единица указывает на необходимость возвращения первого коэффициента линейной зависимости, т.е. m. ЛКМ на ОК на палитре формул.
Функция ЛИНЕЙН возвращает коэффициенты уравнения прямой в виде массива из двух элементов. С помощью функции ИНДЕКС выбирается нужный элемент.
8. F1 – текущая ячейка. Повторить операции пп.1-7, чтобы в итоге в этой ячейке появилась формула
=ИНДЕКС(ЛИНЕЙН(В1:В15;А1:А15);2).
Эту формулу можно ввести и вручную.
Теперь в ячейке F1 – второй коэффициент наилучшей прямой, т.е. n.
9. Найдем коэффициенты показательного приближения
Ячейка G1 – текущая. Повторим операции пп.1-7, но аргументом функции ИНДЕКС выбираем функцию ЛГРФПРИБЛ. Теперь в ячейке G1 содержится первый коэффициент наилучшего показательного приближения, т.е. а. Действуя аналогично, указав третьим параметром функции ИНДЕКС цифру 2, в ячейке Н1 получим второй коэффициент наилучшего показательного распределения, т.е. b.
Для интерполяции или экстраполяции оптимальной кривой без явного определения ее параметров можно использовать функцию ТЕНДЕНЦИЯ для линейной зависимости и РОСТ для показательной зависимости.
Для построения наилучшей кривой другим способом – Сервис – Анализ данных.
10. В списке Инструменты анализа – пункт Регрессия. ЛКМ на ОК.
11. В поле Выходной интервал Y методом протягивания указать диапазон, содержащий значения функции (столбец В).
12. В поле Входной интервал Х указать столбец А.
13. Установить переключатель НовыйРЛ, имя – Результат.
Открыть Расчетный лист Результаты расчета и убедиться, что вычисленные коэффициенты совпали с полученными первым методом.
Практическая часть
Задание 1. Построить многочлен Лагранжа и вычислить его значение в указанных точках.

Задание 2. По таблице задания 1 построить многочлен Ньютона и найти значение в указанных точках.
Задание 3. Для функции, заданной таблицей в задании 1, найти значение производной первого и второго порядков в указанных точках.
Задание 4. Для таблицы метода наименьших квадратов построить квадратичное приближение.
Вопросы к защите лабораторной работы №4
«Приближение функций. Численное дифференцирование»
1. Постановка задач приближения функций.
2. Полиномиальная интерполяция. Многочлен в форме Лагранжа.
3. Многочлен в форме Ньютона.
4. Погрешность интерполяции.
5. Интерполяция с кратными узлами.
6. Метод наименьших квадратов.
7. Численное дифференцирование на основе интерполяции.
ЛАБОРАТОРНАЯ РАБОТА №5
Численное интегрирование
Теоретическая часть
Постановка задачи численного интегрирования. Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой. Обычный прием механической квадратуры состоит в том, что данную функцию f(x) на рассматриваемом отрезке [a, b] заменяют интерполирующей или аппроксимирующей функцией φ(x) простого вида, а затем приближенно полагают:  Функция φ(x) должна быть такова, чтобы интеграл
Функция φ(x) должна быть такова, чтобы интеграл  вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности.
вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности.
Составные квадратурные формулы. Приведем ряд простейших квадратурных формул, используемых в практике численного интегрирования функции f(x) на некотором интервале [a, b], разбитого на n равных отрезков точками a0=a, a1=a+h, a2=a+2h, …, an=a+nh+b, где n=0,1, …, k и  Положим f(xn)=yn=f(a+nh).
Положим f(xn)=yn=f(a+nh).
Формула прямоугольников:
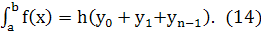
Погрешность формулы определяется выражением:
 где
где  . (15)
. (15)
Формула трапеций:

Погрешность формулы определяется выражением:
 где
где  . (17)
. (17)
Формула Симпсона:

где  . (18)
. (18)
Погрешность формулы определяется выражением:
 где
где  . (19)
. (19)







 Функция φ(x) должна быть такова, чтобы интеграл
Функция φ(x) должна быть такова, чтобы интеграл  вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности.
вычислялся непосредственно. Если функция f(x) заданна аналитически, то ставится вопрос об оценке погрешности. Положим f(xn)=yn=f(a+nh).
Положим f(xn)=yn=f(a+nh).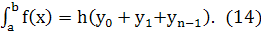
 где
где  . (15)
. (15)
 где
где  . (17)
. (17)
 . (18)
. (18) где
где  . (19)
. (19)


