1.  (антикоммутативность).
(антикоммутативность).
Доказательство: Из определения следует, что векторы  и
и  имеют одинаковую длину и противоположные направления:
имеют одинаковую длину и противоположные направления:
 .
.
2.  (ассоциативность).
(ассоциативность).
Докажем это свойство для 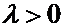 : вектор
: вектор  имеет то же направление, что и вектор
имеет то же направление, что и вектор 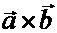 . Вектор
. Вектор  при
при 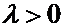 имеет то же направление. Длины этих векторов также совпадают:
имеет то же направление. Длины этих векторов также совпадают:  ,
,  . Аналогично проводится доказательство для случая
. Аналогично проводится доказательство для случая  .
.
3.  (дистрибутивность).
(дистрибутивность).
Без доказательства.
.6. Геометрический смысл векторного произведения: Модуль векторного произведения равен площади параллелограмма, построенного на перемножаемых векторах.
10. Смешанное произведение трех векторов и его геометрический смысл. Условие компланарности векторов.
Определение 4.3. Векторы, параллельные одной плоскости, называются компланарными. Очевидно, что два вектора всегда компланарны.
Теорема. Для того чтобы три вектора были компланарны, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
Определение 4.2. Смешанным произведением трех векторов  ,
,  и
и  называется число, равное
называется число, равное  , т.е. скалярному произведению векторного произведения первых двух на третий вектор.
, т.е. скалярному произведению векторного произведения первых двух на третий вектор.
Свойства смешанного произведения.
1.  .
.
Доказательство этих соотношений проводится аналогично выводу формулы (4). Чтобы их запомнить заметим, что при «циклической перестановке» векторов (вектор передвигается на следующее место, а последний – на первое) знак не меняется, а при перестановке двух соседних векторов знак смешанного произведения меняется.
2. Геометрический смысл смешанного произведения.Модуль смешанного произведения равен объему параллелепипеда, построенного на этих векторах, как на ребрах.
Параметрическое и каноническое уравнения прямой на плоскости.
Так как координаты вектора  и известны координаты вектора
и известны координаты вектора  , то можно записать векторное уравнение прямой (1) в координатах:
, то можно записать векторное уравнение прямой (1) в координатах:  Полученную систему называют параметрическим уравнением прямой.
Полученную систему называют параметрическим уравнением прямой.
Выражая параметр  из каждого уравнения параметрической системы (2), получим
из каждого уравнения параметрической системы (2), получим
 Û
Û 
Опуская  , получим каноническое уравнение прямой:
, получим каноническое уравнение прямой:
 , (3)
, (3)
где 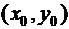 - координаты точки, через которую проходит прямая, а
- координаты точки, через которую проходит прямая, а  - координаты направляющего вектора.
- координаты направляющего вектора.
Приведенное и общее уравнения прямой. Угол между прямыми. Расстояние от точки до прямой. Критерий перпендикулярности.
общее уравнение прямой
 .
.
приведенное уравнение прямой  , где
, где  ,
,  .
.
Таким образом, угол между прямыми находится по формуле:
 . (9)
. (9)
В частности, если угол составляет  , то
, то  . Это возможно, если
. Это возможно, если  . Получаем критерий перпендикулярности прямых
. Получаем критерий перпендикулярности прямых
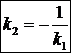 или
или  (10)
(10)
Критерием параллельности двух невертикальных прямых на плоскости  и
и 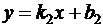 является равенство:
является равенство:
 , (11)
, (11)
т.к. 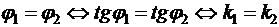 .
.
Уравнения прямой в пространстве.
Прямую в пространстве можно задать как пересечение двух плоскостей, т.е. системой:

Уравнения плоскости в пространстве.
 , где
, где  .
.
Уравнение (5) называется общим уравнением плоскости.



 (антикоммутативность).
(антикоммутативность). и
и  имеют одинаковую длину и противоположные направления:
имеют одинаковую длину и противоположные направления: .
. (ассоциативность).
(ассоциативность).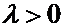 : вектор
: вектор  имеет то же направление, что и вектор
имеет то же направление, что и вектор 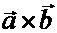 . Вектор
. Вектор  при
при  ,
,  . Аналогично проводится доказательство для случая
. Аналогично проводится доказательство для случая  .
. (дистрибутивность).
(дистрибутивность). ,
,  и
и  называется число, равное
называется число, равное  , т.е. скалярному произведению векторного произведения первых двух на третий вектор.
, т.е. скалярному произведению векторного произведения первых двух на третий вектор. .
. и известны координаты вектора
и известны координаты вектора  , то можно записать векторное уравнение прямой (1) в координатах:
, то можно записать векторное уравнение прямой (1) в координатах:  Полученную систему называют параметрическим уравнением прямой.
Полученную систему называют параметрическим уравнением прямой. из каждого уравнения параметрической системы (2), получим
из каждого уравнения параметрической системы (2), получим Û
Û 
 , (3)
, (3)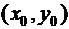 - координаты точки, через которую проходит прямая, а
- координаты точки, через которую проходит прямая, а  - координаты направляющего вектора.
- координаты направляющего вектора. .
. , где
, где  ,
,  .
. . (9)
. (9) , то
, то  . Это возможно, если
. Это возможно, если  . Получаем критерий перпендикулярности прямых
. Получаем критерий перпендикулярности прямых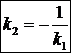 или
или  (10)
(10) и
и 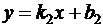 является равенство:
является равенство: , (11)
, (11)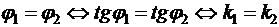 .
.
 , где
, где  .
.


