Сравнение рекурсии и итерации. Оценка сложности вычисления n-го числа Фибоначчи рекурсивным и итерационным способами.

В отличие от итерации, рекурсия не является существенной для программирования на PL/SQL. Любая проблема, которая может быть решена рекурсией, может быть решена и итерацией. Далее, концепцию итерации легче усвоить, поскольку примеры рекурсии не столь часты в повседневной жизни. Как следствие, итеративную версию подпрограммы обычно легче спроектировать, чем рекурсивную версию той же программы. Однако рекурсивная версия обычно проще, меньше, и потому ее легче отладить. Сравните следующие функции, которые вычисляют n-й член ряда Фибоначчи:

-- рекурсивная версия

FUNCTION fib (n POSITIVE) RETURN INTEGER IS

BEGIN

IF (n = 1) OR (n = 2) THEN

RETURN 1;

ELSE

RETURN fib(n - 1) + fib(n - 2);

END IF;

END fib;

 

-- итеративная версия

FUNCTION fib (n POSITIVE) RETURN INTEGER IS

pos1 INTEGER:= 1;

pos2 INTEGER:= 0;

cum INTEGER;

BEGIN

IF (n = 1) OR (n = 2) THEN

RETURN 1;

ELSE

cum:= pos1 + pos2;

FOR i IN 3..n LOOP

pos2:= pos1;

pos1:= cum;

cum:= pos1 + pos2;

END LOOP;

RETURN cum;

END IF;

END fib;

Рекурсивная версия функции fib более элегантна. Однако итеративная версия эффективнее; она работает быстрее и использует меньше памяти. Причина этого в том, что каждый рекурсивный вызов требует дополнительного времени и памяти. Чем больше число рекурсивных вызовов, тем больше разница в эффективности. Тем не менее, если вы ожидаете, что число рекурсивных вызовов будет невелико, можно предпочесть рекурсивную версию из-за ее читабельности.

 

 

Реализация построения кривой Гильберта.

На рисунке кривые первого, второго и третьего порядка.

§ Каждый последующий порядок образуется с предыдущем

§ При переходе на следующий уровень вершины уменьшаются в два раза.

Правило построение кривой: А

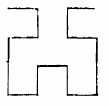В С D

Для реализации, А = gl, B=gu, C = gr, D = gd.

 

program z1;

uses crt,graph;

var a,h,s,ex,x,y,r,d,gm,o:integer;

procedure gd(n:integer);forward;

procedure gu(n:integer);forward;

procedure gr(n:integer);forward;

 

procedure gl(n:integer);

begin

if n>0 then

begin

gd(n-1);x:=x-h;LineTo(x,y);

gl(n-1);y:=y+h;LineTo(x,y);

gl(n-1);x:=x+h;LineTo(x,y);

gu(n-1);

end;

end;

procedure gu(n:integer);

begin

if n>0 then

begin

gr(n-1);y:=y-h;LineTo(x,y);

gu(n-1);x:=x+h;LineTo(x,y);

gu(n-1);y:=y+h;LineTo(x,y);

gl(n-1);

end;

end;

procedure gr(n:integer);

begin

if n>0 then

begin

gu(n-1);x:=x+h;LineTo(x,y);

gr(n-1);y:=y-h;LineTo(x,y);

gr(n-1);x:=x-h;LineTo(x,y);

gd(n-1);

end;

end;

procedure gd(n:integer);

begin

if n>0 then

begin

gl(n-1);y:=y+h;LineTo(x,y);

gd(n-1);x:=x-h;LineTo(x,y);

gd(n-1);y:=y-h;LineTo(x,y);

gr(n-1);

end;

end;

function pow2(a:integer):integer;

var i,p:integer;

begin

p:=1;

for i:=1 to a do p:=p*2;

pow2:=p;

end;

 

begin clrscr;

ex:=1;

while ex=1 do

begin

write('Input Grade Of Graphic ');readln(a);

write('Side of square');readln(s);

write('Orientation(1-u,2-r,3-d,4-l)');readln(o);

d:=Detect;

InitGraph(d,gm,'');

s:=round(s*GetMaxY/100);

h:=round(s/(pow2(a)-1));

x:=GetMaxX div 2;

y:=GetMaxY div 2;

r:=s div 2;

case o of

1: begin

x:=x - r;

y:=y + r;

moveto(x,y);

gu(a);

end;

2:begin

x:=x - r;

y:=y + r;

moveto(x,y);

gr(a);

end;

3: begin

x:=x + r;

y:=y - r;

moveto(x,y);

gd(a);

end;

4: begin

x:=x + r;

y:=y - r;

moveto(x,y);

gl(a);

end;

end;

readln;

closegraph;

Writeln('Proceed? (1/0)');

readln(ex);

end;

 

end

.