В данной работе продемонстрирован процесс создания различных цифровых регуляторов. Созданные цифровые регуляторы предназначены для управления скоростью двигателя постоянного тока. В целях упрощения, контур тока исключен.
Перед тем, как перейти к разработке регулятора для двигателя, попробуем разработать систему регулирования тока в RL-цепочке посредством цифрового регулятора. Для начала разработаем модель RL цепочки за счет численного решения дифференциального уравнения: U=R*i+L*di/dt. Для решения данного уравнения на компьютере его необходимо дискретизировать, то есть перейти к уравнению в конечно-разностной форме и решить его. Технология такого перехода будет показана на примере апериодического звена, которое, как известно, описывается практически той же передаточной функцией, что и RL-цепочка:
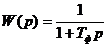 ,
,
где Тф – постоянная времени инерционного звена (фильтра). Если обозначить входной сигнал как 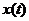 , а выходное управляющее воздействие, подаваемое на вход объекта управления, как
, а выходное управляющее воздействие, подаваемое на вход объекта управления, как 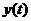 , то передаточной функции инерционного звена будет соответствовать дифференциальное уравнение:
, то передаточной функции инерционного звена будет соответствовать дифференциальное уравнение:
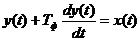 .
.
Особенность расчетов любой цифровой системы, в том числе и при моделирование на ЭВМ в среде Симулинк, состоит в том, что от момента получения информации о состоянии входных величин, в данном случае 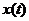 , до момента выдачи, рассчитанного в соответствии с заданным алгоритмом значения управляющего воздействия
, до момента выдачи, рассчитанного в соответствии с заданным алгоритмом значения управляющего воздействия 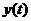 , проходит определенное время. Следующую выборку данных можно получить только спустя некоторое время, называемое интервалом квантования по времени или периодом дискретизации по времени T. Таким образом, входная информация доступна только в фиксированные моменты времени
, проходит определенное время. Следующую выборку данных можно получить только спустя некоторое время, называемое интервалом квантования по времени или периодом дискретизации по времени T. Таким образом, входная информация доступна только в фиксированные моменты времени 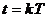 , где
, где  – целое число 0, 1, 2,..., представляющее собой номер очередной выборки данных. Значения входной
– целое число 0, 1, 2,..., представляющее собой номер очередной выборки данных. Значения входной 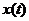 и выходной
и выходной 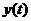 функций определены только в дискретные моменты времени
функций определены только в дискретные моменты времени 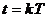 . Такие дискретные функции называются решетчатыми, а уравнения, связывающие между собой дискретные переменные - дискретными разностными уравнениями. Согласно теореме Котельникова (или Шеннона в западном варианте), если цифровой регулятор или цифровой фильтр имеет частоту дискретизации по крайней мере вдвое большую, чем максимальная частота входного сигнала, то он может быть реализован без существенных погрешностей на базе своего аналогового прототипа. При выполнении этого условия существует переход от дифференциального уравнения к разностному — значения непрерывных величин заменяются дискретными, а значения дифференциалов непрерывных функций — так называемыми разностями, то есть величинами приращений дискретных переменных за период дискретизации T.
. Такие дискретные функции называются решетчатыми, а уравнения, связывающие между собой дискретные переменные - дискретными разностными уравнениями. Согласно теореме Котельникова (или Шеннона в западном варианте), если цифровой регулятор или цифровой фильтр имеет частоту дискретизации по крайней мере вдвое большую, чем максимальная частота входного сигнала, то он может быть реализован без существенных погрешностей на базе своего аналогового прототипа. При выполнении этого условия существует переход от дифференциального уравнения к разностному — значения непрерывных величин заменяются дискретными, а значения дифференциалов непрерывных функций — так называемыми разностями, то есть величинами приращений дискретных переменных за период дискретизации T.
Аналогом дифференциала первого порядка для непрерывной функции при этом является первая обратная разность (первая левая разность):

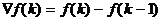 .
.
Для перехода от непрерывного уравнения к разностному заменим непрерывные переменные дискретными, дифференциалы этих переменных – разностями, а приращение времени 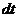 – величиной интервала квантования по времени T. Получим:
– величиной интервала квантования по времени T. Получим:
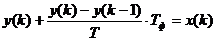 .
.
После преобразований дискретное уравнение примет вид:
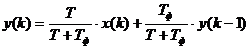 .
.
Обозначим коэффициенты:
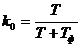 и
и 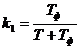 .
.
Тогда, с учетом полученных коэффициентов 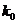 и
и 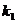 , дискретное уравнение инерционного звена выглядит следующим образом:
, дискретное уравнение инерционного звена выглядит следующим образом:
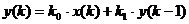
Задание для самостоятельной работы
Перейдите от дифференциального уравнения RL-цепочки U=R*L+L*di/dt к конечно-разностной форме и получите формулу для расчета текущего значения тока.
Реализуем модель RL цепочки посредством механизма S-функции Симулинка. На вход такой S-функции будет подаваться сигнал напряжения, на выходе – сигнал тока. Текст такой S-функции приведен ниже.
float static R=3.6;
float static L=0.034;
float static i=0;
float static di=0;
float static u=0;
float static t=0;
float static dt=0.001;
u=u0[0];// забираем входной сигнал - напряжение
t=t+dt; // расчитываем текущее время
i=i+(u-R*i)/L*dt; // расчитываем ток
y0[0]=i;// выдача результата
Примечание
1. При повторном запуске модели Симулинка, необходимо заново перетранслировать S-функцию посредстом нажатия кнопки Build в окне S-function builder для задания нулевых начальных условий модели. Если применяются несколько компонентов S-функций, необходимо перетранслировать заново каждый перед началом каждого моделирования.
2. float static используется для задания имени новой переменной, применяемой в модели.
При генерации S-функции установите дискретный характер вычислений компонента, период дискретизации 0.001 секунда.
Результаты моделирования показаны на рис.1.
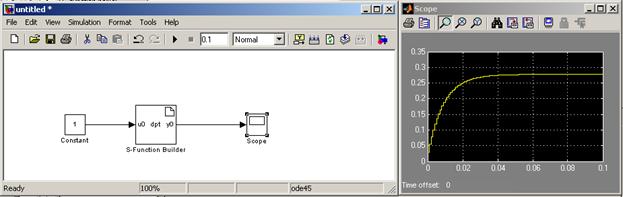
Рис.1.
Повторим моделирование с увеличенным напряжением (рис.2.):
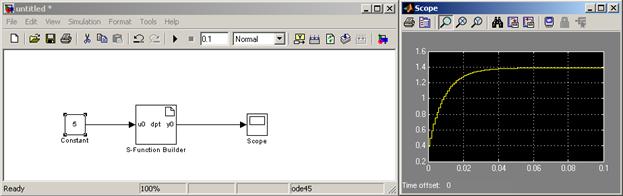
Рис.2
Как можно видеть, при увеличении входного сигнала происходит соответствующее увеличение выходного сигнала, форма выходного сигнала одинакова и соответствует реальному поведению тока в RL-цепочке.
Для регулирования тока можно применить простейший цифровой регулятор, который работает по принципу: если выходной сигнал меньше заданного, то увеличиваем напряжение, если больше – то уменьшаем.
В классической теории автоматического управления принято управлять по ошибке (рассогласованию между входной и выходной координатами). С учетом этого, указанный принцип несколько модифицируется:
если ошибка по току меньше нуля, то уменьшаем текущее напряжение на определенное значение, если больше – то увеличиваем.
Для реализации регулятора создадим S-функцию reg, содержимое которой представлено ниже.
float static input=0;
float static output=0;
input=u0[0];
if (input<0) output=output-0.01;
if (input>0) output=output+0.01;
y0[0]=output;
Создадим систему управления током RL-цепочки с использованием этих разработанных S-функций. Модель системы управления показана на рис.3. Как можно видеть, для регулирования используется сигнал обратной связи по току, который вычитается из заданного сигнала. При этом в обратной связи применен компонент Z-1, который обеспечивает задержку в передаче выходного сигнала на сумматор на одну дискрету, то есть на сумматор подается значение, которое было рассчитано при предыдущем шаге расчета.
Задание для самостоятельной работы
В показанной модели установите время моделирования inf (бесконечность), запустите моделирование, и изменяя задания на ток, наблюдайте его изменение в модели RL-цепочки.
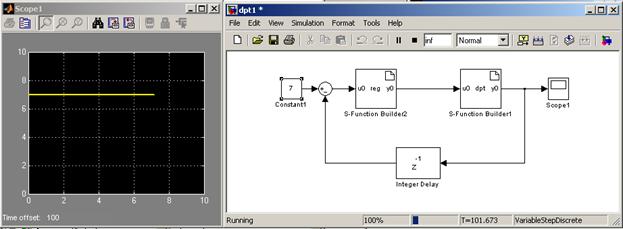
Рис.3
Перейдем теперь к разработке цифровой системы управления двигателем постоянного тока. За основу возьмем двигатель 2ПБ132МГ со следующими характеристиками:
Номинальная мощность 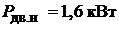 .
.
Номинальное напряжение 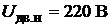 .
.
Сопротивление якорной цепи  .
.
Индуктивность якорной цепи 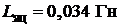 .
.
Момент инерции двигателя 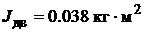 .
.
Коэффициент ЭДС при номинальном потоке возбуждения 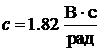 .
.
Изначально необходимо создать модель двигателя.
ДПТ может быть описан дифференциальными уравнениями

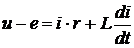 ,
,
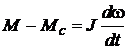 ,
,
где 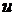 – напряжение на якоре, В;
– напряжение на якоре, В;
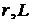 – активное сопротивление, Ом; индуктивность якорной цепи, Гн;
– активное сопротивление, Ом; индуктивность якорной цепи, Гн;
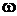 – угловая скорость вращения двигателя,
– угловая скорость вращения двигателя, 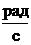 ;
;
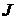 – момент инерции якоря двигателя;
– момент инерции якоря двигателя;
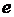 – ЭДС двигателя, В;
– ЭДС двигателя, В;
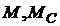 – момент двигателя и статической нагрузки,
– момент двигателя и статической нагрузки, 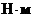 ;
;
Момент и ЭДС двигателя определяются по выражениям:
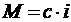 ;
;
Задание для самостоятельной работы
Преобразуйте дифференциальные уравнения, описывающие поведение двигателя постоянного тока в конечно-разностную форму и предложите формулу для расчета тока и скорости двигателя.
Реализация модели двигателя постоянного тока с помощью S-функции может быть выполнена следующим образом:
float static R=3.6;
float static L=0.034;
float static i=0;
float static u=0;
float static t=0;
float static dt=0.001;
float static w=0;
float static Mc=0;
float static Me=0;
float static c=1.82;
float static J=0.038+0.0;
u=u0[0];// забираем входной сигнал - напряжение
Mc=u1[0];
t=t+dt; // расчитываем текущее время
i=i+(u-R*i-c*w)/L*dt; // расчитываем ток
Me=i*c;
w=w+(Me-Mc)/J*dt;
y0[0]=i;// выдача результата
y1[0]=w;
Для регулирования скорости применим тот же самый регулятор, который был разработан для RL-цепочки. С учетом ограничения на максимальное напряжение, которое можно приложить к двигателю, введем программное ограничение на выходное значение регулятора. Текст программы такого регулятора с ограничением выходного значения показан ниже:
float static input=0;
float static output=0;
input=u0[0];
if (input<0) output=output-0.01;
if (input>0) output=output+0.01;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Задание для самостоятельной работы
Соберите модель, показанную на рис.4., установите время моделирования 10 секунд и смоделируйте пуск двигателя при различных заданиях на скорость (компонент Constatnt) и заданиях на момент (компонент Constant2).
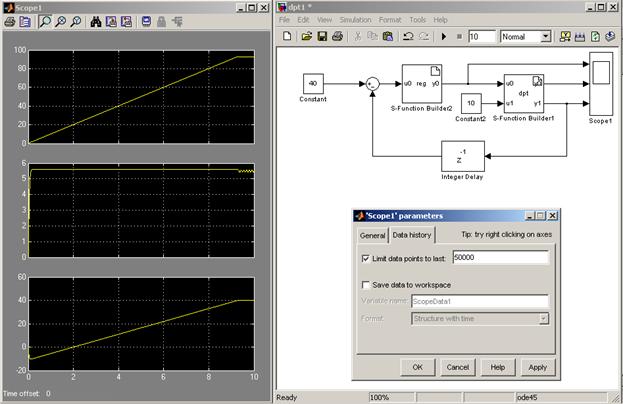
Рис.4.
Как можно увидеть при выполнении задания, двигатель выходит на заданную скорость при задании различных моментов, то есть система астатична, что объясняется интегрирующими свойствами примененного регулятора. Недостатком данного регулятора является низкое быстродействие – время выхода на заданную скорость составляет порядка 10 секунд (см.рис.4).
Задание для самостоятельной работы
Предложите свой способ увеличения быстродействия системы.
Применим пропорциональный регулятор с коэффициентом усиления 10. Для этого содержимое S-функции регулятора должно принять следующий вид:
float static input=0;
float static output=0;
input=u0[0];
output=10*input;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Установите время моделирования 0,2 секунды. В результате должны получиться графики переходных процессов, идентичные представленным на рис.5. Как видно из графиков, установившаяся скорость отличается от заданной (42 против 50). При увеличении нагрузки (рис.6) различие увеличивается. Данный пример демонстрирует отсутствие астатизма П-регулятора.
Задание для самостоятельной работы
Предложите способ уменьшения ошибки регулирования при применении П-регулятора.
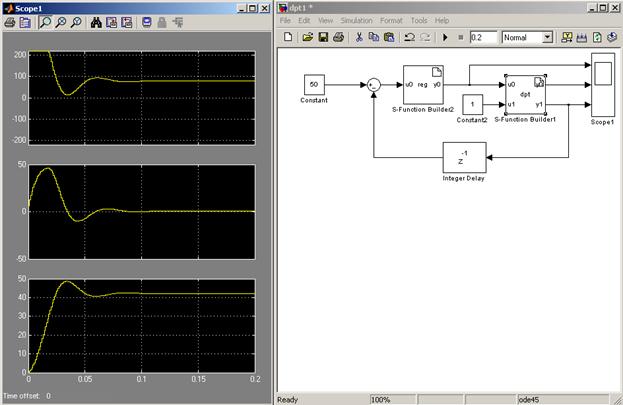
Рис.5
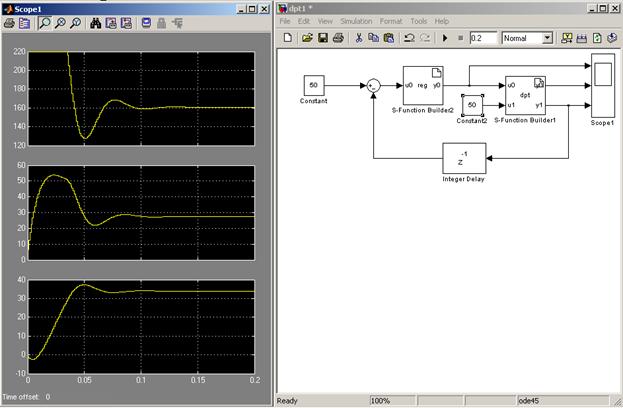
Рис.6
Еще одним простейшим регулятором является релейный. Его реализация будет выглядеть следующим образом:
float static input=0;
float static output=0;
input=u0[0];
if (input<0) output=-220;
if (input>=0) output=220;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Релейный регулятор характеризуется резкими переключениями при регулировании, что ведет к колебательности процессов при срабатываний регулятора (см.рис.7).
Задание для самостоятельной работы
1. Упростите предложенный регулятор.
2. Изменяя задание на скорость и момент нагрузки, определите, является ли релейный регулятор астатичным.
3. Предложите способы устранения колебаний координат управляемой системы, возникаемых при работе релейного регулятора.
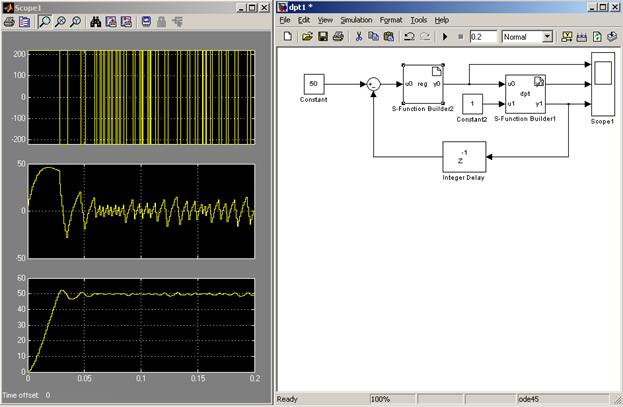
Рис.7
Одним из способов устранения недостатков работы релейного регулятора является введение зоны гистерезиса. Реализация такого регулятора будет следующей (ширина гистерезиса – от -3 до 3):
float static input=0;
float static output=0;
input=u0[0];
if (input<-3) output=-220;
if (input>3) output=220;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Результат работы такого регулятора показан на рис.8.
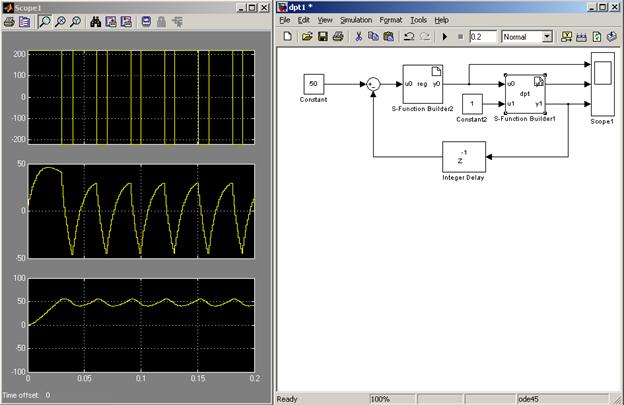
Рис.8
На практике очень распространен ПИ-регулятор.
Передаточная функция непрерывного ПИ-регулятора, реализуемого на аналоговой технике (например, на базе операционных усилителей), имеет вид:
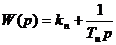 ,
,
где 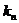 – коэффициент передачи пропорциональной части,
– коэффициент передачи пропорциональной части, 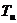 – постоянная интегрирования. Если обозначить входной сигнал, который обычно является величиной рассогласования между заданным значением регулируемой величины и ее фактическим значением, снимаемым с датчика обратной связи, как
– постоянная интегрирования. Если обозначить входной сигнал, который обычно является величиной рассогласования между заданным значением регулируемой величины и ее фактическим значением, снимаемым с датчика обратной связи, как  , а выходное управляющее воздействие, подаваемое на вход объекта управления, как
, а выходное управляющее воздействие, подаваемое на вход объекта управления, как 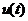 , то передаточной функции ПИ-регулятора будет соответствовать дифференциальное уравнение:
, то передаточной функции ПИ-регулятора будет соответствовать дифференциальное уравнение:
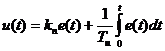 .
.
Продифференцируем исходное уравнение непрерывного ПИ-регулятора, чтобы избавиться от интеграла:
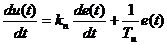 .
.
Для перехода от непрерывного уравнения к разностному заменим непрерывные переменные дискретными, дифференциалы этих переменных – разностями, а приращение времени 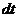 – величиной интервала квантования по времени T. Получим:
– величиной интервала квантования по времени T. Получим:
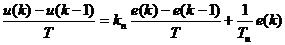 .
.
После очевидных алгебраических преобразований разностное уравнение ПИ-регулятора примет вид:
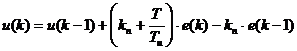 .
.
Обозначим коэффициенты:
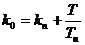 и
и 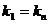 .
.
С учетом полученных коэффициентов уравнение будет выглядеть следующим образом:
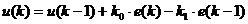 .
.
На рис.9 представлена структурная схема ПИ-регулятора с неявновыраженной интегральной составляющей и общим ограничением, где Звено 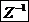 — запаздывание на такт.
— запаздывание на такт.
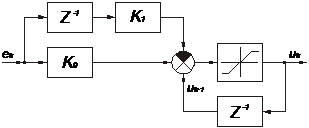
Рис.9
Реализация ПИ-регулятора в Симулинке выглядит следующим образом:
float static input=0;
float static output=0;
float static k0=2+0.001/0.01;
float static k1=2;
float static input_prev=0;
input=u0[0];
output=output+k0*input-k1*input_prev;
input_prev=input;
if (output>220) output=220;
if (output<-220) output=-220;
y0[0]=output;
Как видно из рис.10 и 11, при работе ПИ-регулятора ошибка регулирования для установившегося значения, в отличии от П-регулятора, равна практически нулевому значению при различных моментах сопротивления нагрузки.

Рис.10
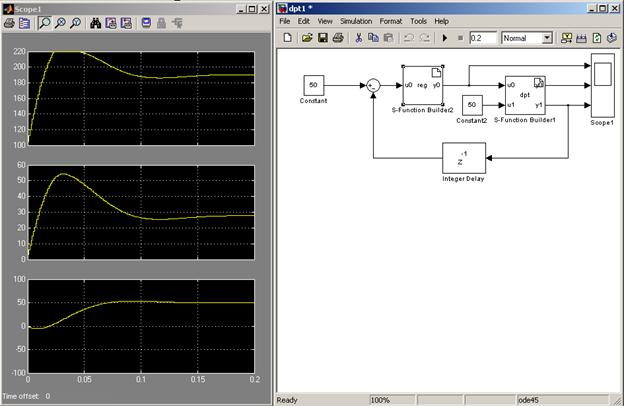
Рис.11
Задание для самостоятельной работы
Введите контур тока в рассматриваемую модель и реализуйте его на базе ПИД-регулятора.



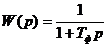 ,
,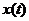 , а выходное управляющее воздействие, подаваемое на вход объекта управления, как
, а выходное управляющее воздействие, подаваемое на вход объекта управления, как 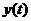 , то передаточной функции инерционного звена будет соответствовать дифференциальное уравнение:
, то передаточной функции инерционного звена будет соответствовать дифференциальное уравнение: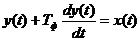 .
.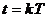 , где
, где  – целое число 0, 1, 2,..., представляющее собой номер очередной выборки данных. Значения входной
– целое число 0, 1, 2,..., представляющее собой номер очередной выборки данных. Значения входной 
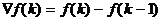 .
.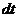 – величиной интервала квантования по времени T. Получим:
– величиной интервала квантования по времени T. Получим: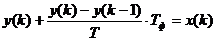 .
.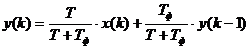 .
.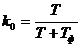 и
и 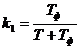 .
.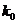 и
и 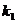 , дискретное уравнение инерционного звена выглядит следующим образом:
, дискретное уравнение инерционного звена выглядит следующим образом: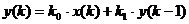



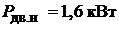 .
.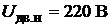 .
. .
.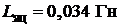 .
.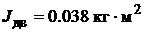 .
.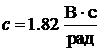 .
.
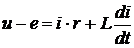 ,
,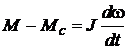 ,
,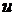 – напряжение на якоре, В;
– напряжение на якоре, В;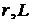 – активное сопротивление, Ом; индуктивность якорной цепи, Гн;
– активное сопротивление, Ом; индуктивность якорной цепи, Гн;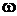 – угловая скорость вращения двигателя,
– угловая скорость вращения двигателя, 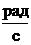 ;
;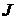 – момент инерции якоря двигателя;
– момент инерции якоря двигателя;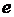 – ЭДС двигателя, В;
– ЭДС двигателя, В;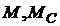 – момент двигателя и статической нагрузки,
– момент двигателя и статической нагрузки, 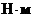 ;
;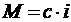 ;
;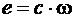





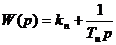 ,
,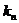 – коэффициент передачи пропорциональной части,
– коэффициент передачи пропорциональной части, 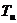 – постоянная интегрирования. Если обозначить входной сигнал, который обычно является величиной рассогласования между заданным значением регулируемой величины и ее фактическим значением, снимаемым с датчика обратной связи, как
– постоянная интегрирования. Если обозначить входной сигнал, который обычно является величиной рассогласования между заданным значением регулируемой величины и ее фактическим значением, снимаемым с датчика обратной связи, как  , а выходное управляющее воздействие, подаваемое на вход объекта управления, как
, а выходное управляющее воздействие, подаваемое на вход объекта управления, как 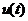 , то передаточной функции ПИ-регулятора будет соответствовать дифференциальное уравнение:
, то передаточной функции ПИ-регулятора будет соответствовать дифференциальное уравнение: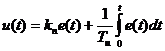 .
.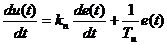 .
.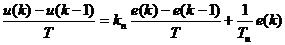 .
.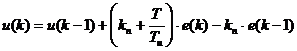 .
.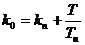 и
и 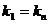 .
.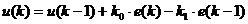 .
. — запаздывание на такт.
— запаздывание на такт.





