Цели:
– научиться вычислять арккосинус числа a;
– научиться находить значения арккосинусов отрицательных чисел через значения арккосинусов положительных чисел;
– научиться решать простейшие уравнения вида
Оснащение занятия: учебник, конспект, справочник.
Порядок выполнения работы:
Задание 1. Повторение теоретического материала.
1. Какова область значений косинуса?
2. При каком значении, а, уравнение имеет корни?
3. По какой формуле находятся корни уравнения?
4. Сколько корней имеет уравнение и почему?
5. Что называется, арккосинусом числа, а?
6. По какой формуле можно находить значения арккосинусов отрицательных чисел через значения арккосинусов положительных чисел?
Задание 2. Выполните № 568 (неч.), № 569 (неч.), № 571-№ 573 (неч.).
Задание 3. Запишите формулу сложения и выполните №574.
Задание 4. Разберите решение задачи 4 (стр.167) и выполните № 576 (неч.).
Литература: Алимов Ш. А. Алгебра и начала анализа стр. 165.
Практическая работа № 29
Тема: Методы решения тригонометрических уравнений
Цели:
– научиться решать тригонометрические уравнения
а) сводящиеся к квадратным;
б) уравнение вида;
в) разложением левой части на множители.
– рассмотреть решение системы тригонометрических уравнений.
Оснащение занятия: учебник, конспекты, справочник.
Порядок выполнения работы:
Задание 1. Организуйте работу парами и ответьте на вопросы:
– Какие тригонометрические уравнения называются простейшими?
– Что понимают под решением тригонометрического уравнения?
– По каким формулам находятся решения простейших тригонометрических уравнений?
– Перечислите основные способы решения тригонометрических уравнений.
– Как решаются уравнения, сводящиеся к квадратным?
– Как решаются уравнения вида?
Задание 2. Вспомните, как решаются уравнения, сводящиеся к квадратным?
Решите уравнение: В-1. № 621(1), № 622 (3). В-2. № 621 (3), № 622(4).
Задание 3. Вспомните, как решаются уравнения вида аsin x+ вcosx =c?
Решите уравнение: В-1. № 624 (3), № 663 (1). В – 2. № 624(2), № 663(3).
Задание 4.
а) Вспомните формулы: сумма и разность синусов, сумма и разность косинусов и решите уравнение: В-1 № 626(2). В-2. № 626(1).
б) Каким способом можно решить следующее уравнение?
В-1. №660 (1), В-2 № 660(3).
в) Для каких углов не определен?
Выполните В-1. №612(6) В-2. №612(5).
Задание 5. Разберите решение задачи 15 на стр.188 и решите в парах № 645.
Дополнительное задание № 678 (1, 3, 4).
Литература: Алимов Ш. А. Алгебра и начала анализа стр.181.
Практическая работа № 30
Тема: Вычисление пределов
Цель: закрепить навыки вычисления пределов
Предел функции. ЧислоL называется пределом функции y = f (x) при x, стремящемся к a:
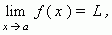 если для любого
если для любого 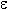 > 0 найдётся такое положительное число
> 0 найдётся такое положительное число 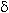 =
= 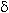 (
(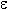 ), зависящее от
), зависящее от 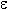 , чтоиз условия | x - a | <
, чтоиз условия | x - a | < 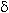 следует | f (x) – L | <
следует | f (x) – L | < 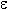 .
.
Это определение означает, что L есть предел функции y = f (x), если значение функции неограниченно приближается к L, когда значение аргумента x приближается к a. Геометрически это значит, что для любого 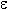 > 0 можно найти такое число
> 0 можно найти такое число 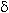 , что если x находится в интервале (a -
, что если x находится в интервале (a - 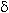 , a +
, a + 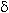 ), то значение функции лежит в интервале (L -
), то значение функции лежит в интервале (L - 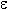 , L +
, L + 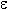 ). Отметим, что в соответствии с этим определением аргумент функции лишь приближается к a, не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.
). Отметим, что в соответствии с этим определением аргумент функции лишь приближается к a, не принимая этого значения! Это следует учитывать при вычислении предела любой функции в точке её разрыва, где функция не существует.
Пример. Найти
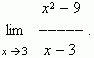
Решение.Подставляя х = 3 в выражение 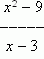 получим не имеющее смысла выражение
получим не имеющее смысла выражение 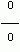 . Поэтому решим по-другому:
. Поэтому решим по-другому:
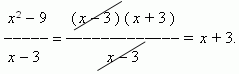
Сокращение дроби в данном случае корректно, так как x  3, он лишь приближается к 3. Теперь мы имеем:
3, он лишь приближается к 3. Теперь мы имеем: 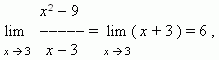
поскольку, еслиx стремится к 3, то x + 3 стремится к 6.
Замечательные пределы
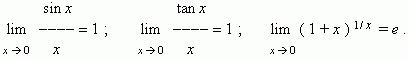
Бесконечно малая и бесконечно большая величины. Если предел некоторой переменной равен 0, то эта переменная называется бесконечно малой.
П р и м е р. Функция y = 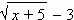 является бесконечно малой при x,
является бесконечно малой при x,
стремящемсяк 4, так как 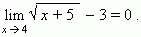
Если абсолютное значение некоторой переменной неограниченно возрастает, то эта переменная называется бесконечно большой.

Бесконечно большая величина не имеет конечного предела, но она имеет так называемый бесконечный предел, что записывается как:
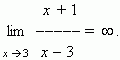
Символ 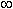 (“бесконечность”) не означает некоторого числа, он означает только, что дробьнеограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может бытькак положительной (при x > 3), так и отрицательной (при x < 3). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x
(“бесконечность”) не означает некоторого числа, он означает только, что дробьнеограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может бытькак положительной (при x > 3), так и отрицательной (при x < 3). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x 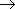 0 функция y = x- 2 бесконечно большая, но она положительна как при x > 0, так и при x < 0; это выражается так:
0 функция y = x- 2 бесконечно большая, но она положительна как при x > 0, так и при x < 0; это выражается так:
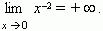
Наоборот, функция y = - x - 2 всегда отрицательна, поэтому 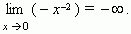
В соответствии с этим, результат в нашем примере можно записать так: 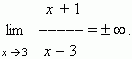

Самостоятельная работа
Вариант 1.
1.Найдите пределы последовательностей:
1. 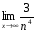 ; 3)
; 3) 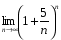 ;
;
2. 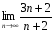 ; 4)
; 4) 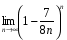 .
.
2.Найдите пределы функций:
1. 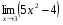 ;
;
2. 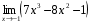 ;
;
3. 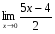 ;
;
4. 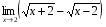 ;
;
5. 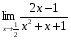 .
.
3. Раскрытие неопределенностей вида 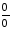 . Найдите пределы:
. Найдите пределы:
1. 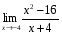 ; 3)
; 3) 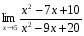 ;
;
2) 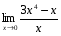 ; 4)
; 4) 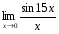 .
.
4. Раскрытие неопределенностей вида 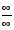 . Найдите пределы:
. Найдите пределы:
1) 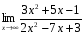 ; 2)
; 2) 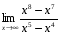 .
.
Практическая работа № 31
Тема: Производная функции
Цели:
– научиться находить производную, используя определение производной;
– научиться находить производную степенной функции;
– научиться находить производную, используя правила дифференцирования.
Оснащение занятия: учебники, конспекты, таблица производных.
Порядок выполнения работы
Задание 1. Дайте определение производной функции и запишите её формулу.
Задание 2. Выполните в парах №780(1,3).
Задание 3.Повторите формулы для нахождения производной степенной функции.
Задание 4.Выполните №787-№790(нечётные).
Задание 5.Запишите формулу 2 на с.233 и рассмотрите решение задачу 4 на с.234.
Задание 6. Выполните №791-№792(неч.).
Задание 7. Рассмотрите решение задачи 3, стр.233 и выполните №793(неч.).
Задание 8. Используя правила дифференцирования суммы, произведения и частного
выполните № 803(неч.), № 810(1,2),№814.
Контроль знаний студентов
Вариант-1. № 806(1,2), № 809(3), № 811(1), № 815(2), №825(1), №826(2,3).
Вариант-2. № 806(3,4), № 809(5), № 811(2), № 815(1), №825(2), №826(1,4).
Литература: Алимов Ш. А. Алгебра и начала анализа стр.225, стр.232, стр.236.
Вариант-1. № 869(5;8), № 871(1), № 872(5), № 873(3), № 876(4).
Вариант-2. № 869(6;7), № 871(3), № 872(3), № 873(4), № 876(1).
Литература: Алимов Ш. А. Алгебра и начала анализа стр.238, стр.241.
Практическая работа № 32



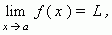 если для любого
если для любого 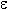 > 0 найдётся такое положительное число
> 0 найдётся такое положительное число 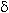 =
= 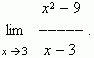
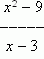 получим не имеющее смысла выражение
получим не имеющее смысла выражение 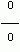 . Поэтому решим по-другому:
. Поэтому решим по-другому: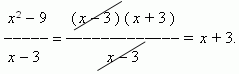
 3, он лишь приближается к 3. Теперь мы имеем:
3, он лишь приближается к 3. Теперь мы имеем: 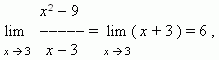
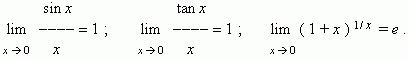
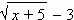 является бесконечно малой при x,
является бесконечно малой при x,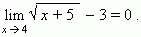

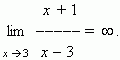
 (“бесконечность”) не означает некоторого числа, он означает только, что дробьнеограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может бытькак положительной (при x > 3), так и отрицательной (при x < 3). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x
(“бесконечность”) не означает некоторого числа, он означает только, что дробьнеограниченно возрастает при x, стремящемся к 3. Следует отметить, что дробь может бытькак положительной (при x > 3), так и отрицательной (при x < 3). Если бесконечно большая величина может быть только положительной при любых значениях x, это отражается в записи. Например, при x 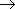 0 функция y = x- 2 бесконечно большая, но она положительна как при x > 0, так и при x < 0; это выражается так:
0 функция y = x- 2 бесконечно большая, но она положительна как при x > 0, так и при x < 0; это выражается так: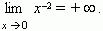
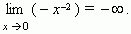
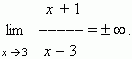

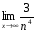 ; 3)
; 3) 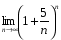 ;
;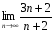 ; 4)
; 4) 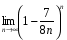 .
.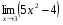 ;
;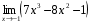 ;
;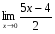 ;
;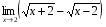 ;
;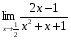 .
.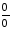 . Найдите пределы:
. Найдите пределы: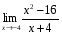 ; 3)
; 3) 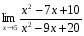 ;
;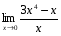 ; 4)
; 4) 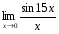 .
.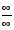 . Найдите пределы:
. Найдите пределы: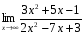 ; 2)
; 2) 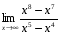 .
.


