Определение центра тяжести плоских фигур.

Цель работы – определить центр тяжести сложной фигуры аналитическим и опытным путями.

Теоретическое обоснование. Материальные тела состоят из элементарных частиц, положение которых в пространстве определяется их координатами. Силы притяжения каждой частицы к Земле можно считать системой параллельных сил, равнодействующая этих сил называется силой тяжести тела или весом тела. Центр тяжести тела – это точка приложения силы тяжести.

Центр тяжести – это геометрическая точка, которая может быть расположена и вне тела (например, диск с отверстием, полый шар и т.п.). Большое практическое значение имеет определение центра тяжести тонких плоских однородных пластин. Их толщиной обычно можно пренебречь и считать, что центр тяжести расположен в плоскости. Если координатную плоскость xOy совместить с плоскостью фигуры, то положение центра тяжести определяется двумя координатами:

;

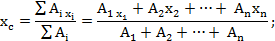
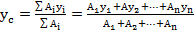где 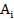- площадь части фигуры, ();

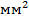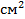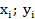– координаты центра тяжести частей фигуры, мм (см).

 

Сечение фигуры	А, мм2	Xc,мм	Yc, мм
	bh	b/2	h/2
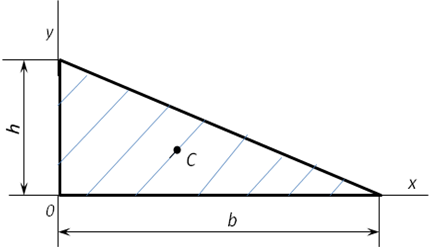
	bh/2	b/3	h/3
	R2a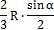
При 2α = π πR2 /2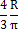

 

Порядок проведения работы.

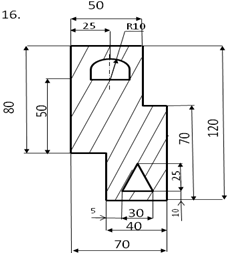
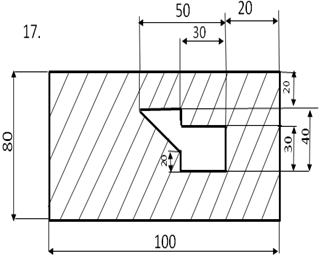
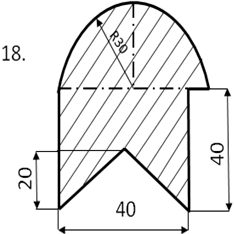
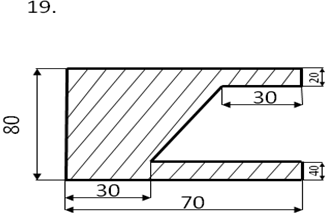
Начертить фигуру сложной формы, состоящую из 3-4 простых фигур (прямоугольник, треугольник, круг и т.п.) в масштабе 1:1 и проставить ее размеры.

Провести оси координат так, чтобы они охватывали всю фигуру, разбить сложную фигуру на простые части, определить площадь и координаты центра тяжести каждой простой фигуры относительно выбранной системы координат.

Вычислить координаты центра тяжести всей фигуры аналитически. Вырезать данную фигуру из тонкого картона или фанеры. Просверлить два отверстия, края отверстий должны быть гладкими, а диаметр отверстий несколько больше диаметра иглы для подвешивания фигуры.

Подвесить фигуру сначала в одной точке (отверстии), прочертить карандашом линию, совпадающую с нитью отвеса. То же повторить при подвешивании фигуры в другой точке. Центр тяжести фигуры, найденный опытным путем, должны совпадать.

Задание

Задача

Определить координаты центра тяжести тонкой однородной пластины аналитически. Проверку произвести опытным путем

 

Алгоритм решения

1. Аналитический способ.

а) Чертеж вычертить в масштабе 1:1.

б) Сложную фигуру разбить на простые

в) Выбрать и провести оси координат (если фигура симметричная, то – по оси симметрии, в противном случае – по контору фигуры)

г) Вычислить площадь простых фигур и всей фигуры

д) Отметить положение центра тяжести каждой простой фигуры на чертеже

е) Вычислить координаты центра тяжести каждой фигуры

(по оси x и y)

ж) Вычислить координаты центра тяжести всей фигуры по формуле

з) Отметить положение центра тяжести на чертеже С (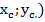

2. Опытное определение.

Правильность решения задачи проверить опытным путем. Вырезать данную фигуру из тонкого картона или фанеры. Просверлить три отверстия, края отверстий должны быть гладкими, а диаметр отверстий несколько больше диаметра иглы для подвешивания фигуры.

Подвесить фигуру сначала в одной точке (отверстии), прочертить карандашом линию, совпадающую с нитью отвеса. То же повторить при подвешивании фигуры в других точках. Значение координат центра тяжести фигуры, найденных при подвешивании фигуры в двух точках: 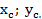. Центр тяжести фигуры, найденный опытным путем, должны совпадать.

3.Заключение о положении центра тяжести при аналитическом и опытном определении.

 

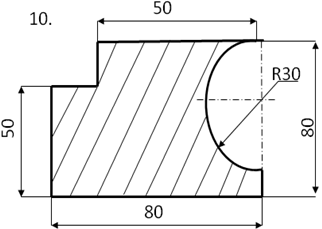
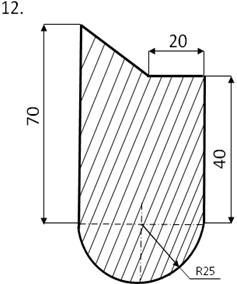
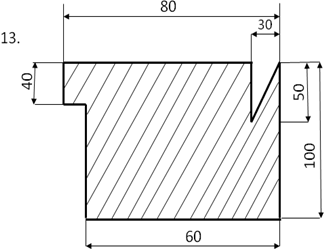
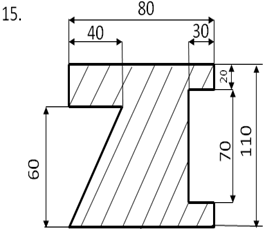
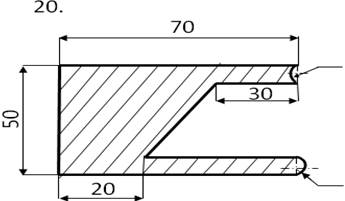
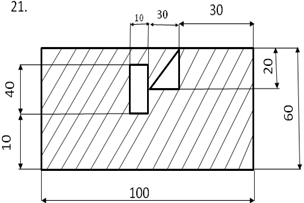
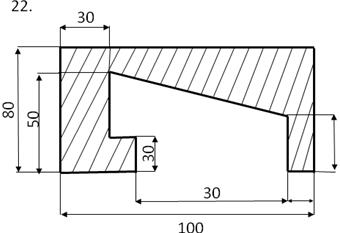
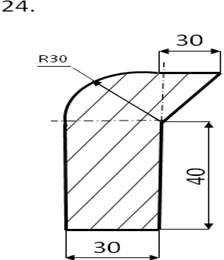
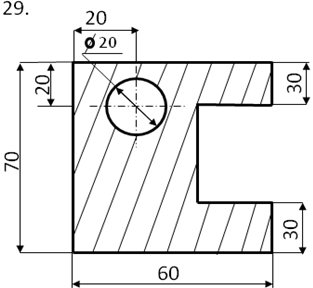
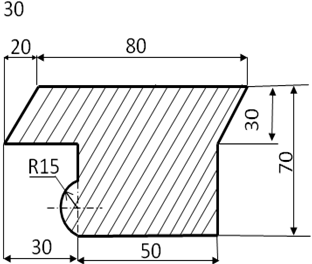
Задание

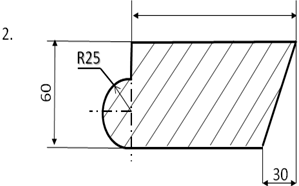
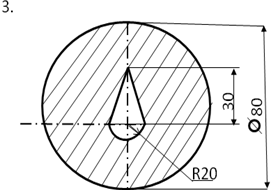
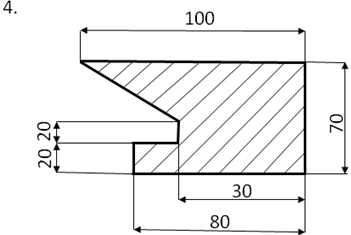
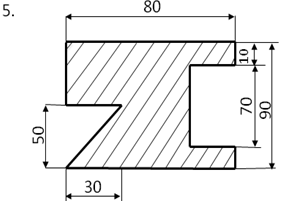
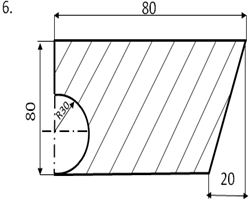
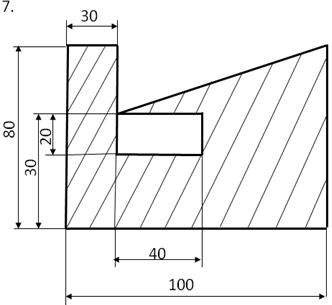
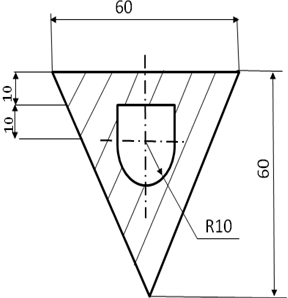
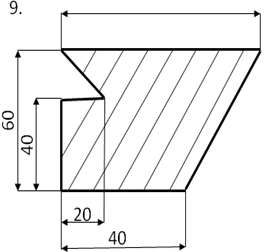
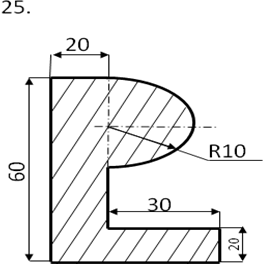
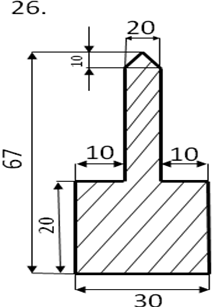
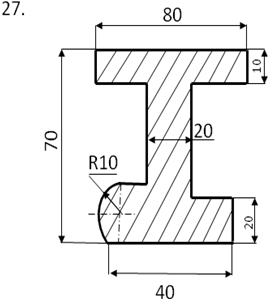
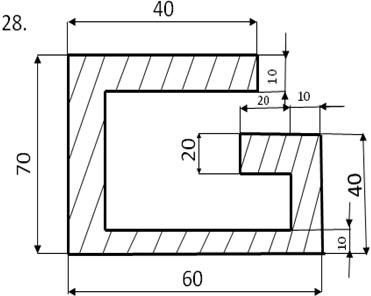
Определить центр тяжести плоского сечения аналитическим и опытным путем.

 

 

 

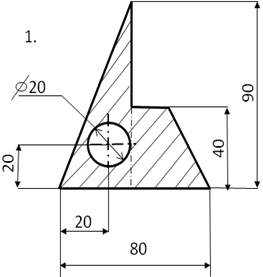
Пример выполнения

Задача

Определить координаты центра тяжести тонкой однородной пластины.

 

 

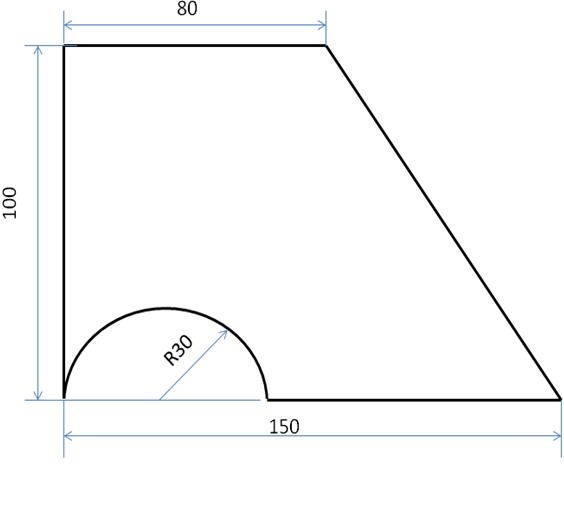
Решение

I Аналитический способ

1. Чертеж вычерчивается в масштабе (размеры обычно даны в мм)

2. Сложную фигуру разбиваем на простые.

1- Прямоугольник

2- Треугольник (прямоугольник)

3- Площадь полуокружности (ее нет, знак минус).

Находим положение центра тяжести простых фигур точек 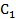, 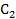и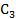

 

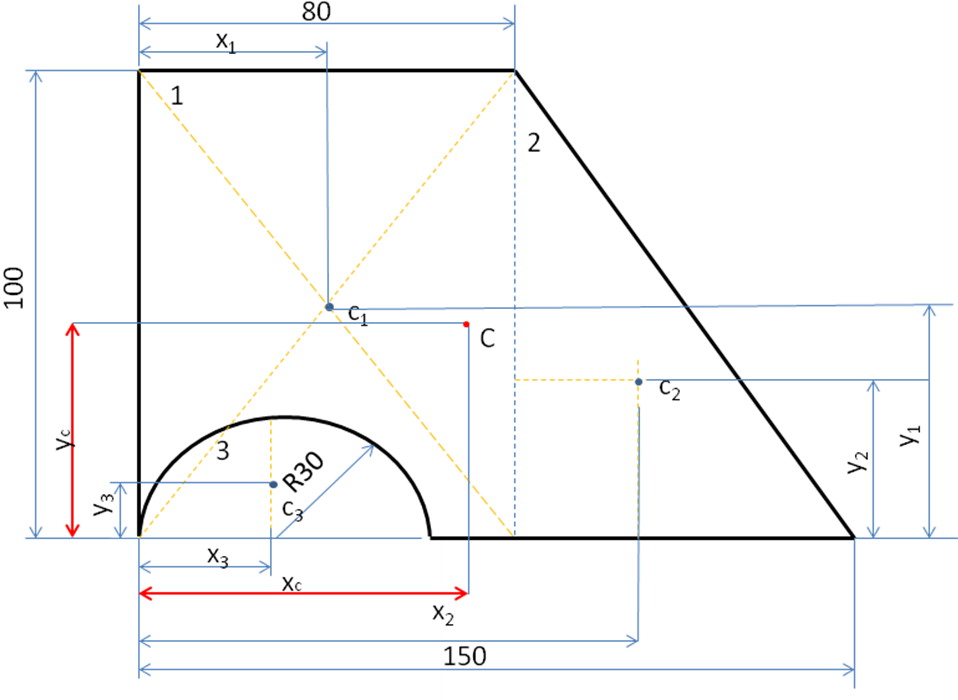
3. Проводим оси координат как удобно и отмечаем начало координат т. О.

4. Вычисляем площади простых фигур и площадь всей фигуры. [размер в см]

(3. нет, знак -).

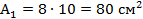
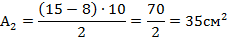
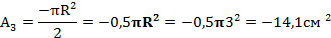
Площадь всей фигуры

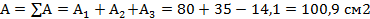
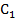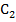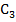5. Находим координату ц.т. , и на чертеже.

6. Вычисляем координаты точек C₁, C₂ и C₃

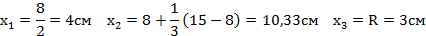
7. Вычисляем координаты точки C

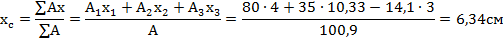
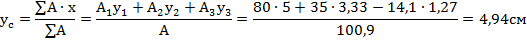
8. На чертеже отмечаем точку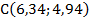

 

II Опытным путем

 

 

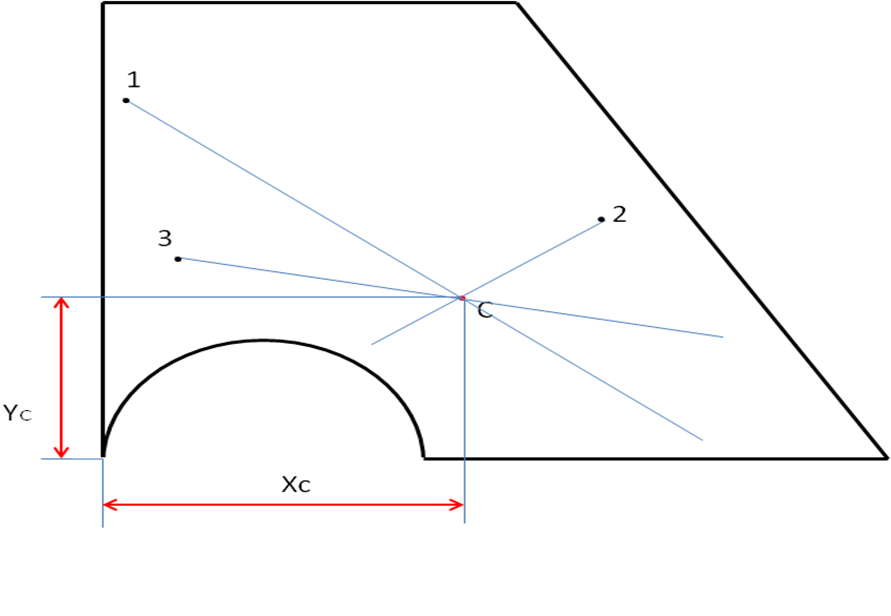
Координаты центра тяжести опытным путем .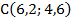

 

Контрольные вопросы.

1. Можно ли рассматривать силу тяжести тела как равнодействующую систему параллельных сил?

2. Может ли располагаться центр тяжести все самого тела?

3. В чем сущность опытного определения центра тяжести плоской фигуры?

4. Как определяется центр тяжести сложной фигуры, состоящей из нескольких простых фигур?

5. Как следует рационально производить разбиение фигуры сложной формы на простые фигуры при определении центра тяжести всей фигуры?

6. Какой знак имеет площадь отверстий в формуле для определения центра тяжести?

7. На пересечении каких линий треугольника находится его центр тяжести?

8. Если фигуру трудно разбить на небольшое число простых фигур, какой способ определения центра тяжести может дать наиболее быстрый ответ?

 

 

Практическая работа №6

 

«Решение задач комплексного характера»

Цель работы: уметь решать задачи комплексного характера (кинематика, динамика)

Теоретическое обоснование: Скорость есть кинематическая мера движения точки, харак­теризующая быстроту изменения ее положения. Скорость точки представляет собой вектор, характеризующий быстроту и направление движения точки в данный момент времени. При задании движения точки уравнениями проекции скорости на оси декартовых координат равны:

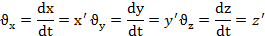
Модуль скорости точки определяется по формуле

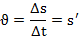
Направление скорости определяется направляющими косинусами:

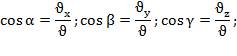
Характеристикой быстроты изменения скорости является ускорение а. Ускорение точки равно производной от вектора скорости по времени:

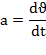
При задании движения точки уравнения проекции ускорения на координатные оси равны:

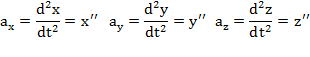
Модуль ускорения:

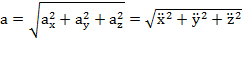
Модуль полного ускорения

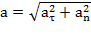
Модуль касательного ускорения определяется по формуле

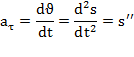
Модуль нормального ускорения определяется по формуле

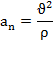
где – радиус кривизны траектории в данной точке.

Направление ускорения определяется направляющими косинусами

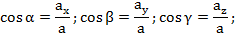
Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид

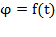
Угловая скорость тела:

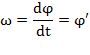
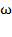Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой . Зависимость между и имеет вид

 

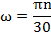
Угловое ускорение тела:

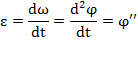
Сила, равная произведению массы данной точке на ее ускорение и направление в сторону прямопротивоположную ускорению точки, называется силой инерции.

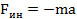
Мощностью называется работа, выполненная силой в единицу времени

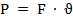
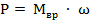
Основное уравнение динамики для вращательного движения

,

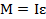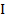– момент инерции тела относительно оси вращения, есть сумма произведений масс материальных точек на квадрат расстояний их до этой оси

 

 

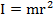
Задание

Тело массой m с помощью троса, наматываемого на барабан диаметром d, перемещается вверх или вниз по наклонной плоскости с углом наклона α. Уравнение движения тела S=f(t), уравнение вращения барабана 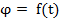, где S в метрах; φ - в радианах; t – в секундах. P и ω - соответственно мощность и угловая скорость на валу барабана в момент конца разгона или начала торможения. Время t₁ – время разгона (из состояния покоя до заданной скорости) или торможения (от заданной скорости до остановки). Коэффициент трения скольжения между телом и плоскостью –f. Потерями на трение на барабане, а также массой барабана пренебречь. При решении задач принять g=10 м/с²

№ вар	α, град	Закон движения	Напр движ	m, кг	t1, c	d, м	P, кВт	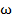, рад/с	f	Опред. величины
		S=0,8t2	Вниз	-	-	0,20	4,0		0,20	m,t1
		φ=4t2	Вниз		1,0	0,30	-	-	0,16	P,ω
		S=1,5t-t2	вверх	-	-	-	4,5		0,20	m, d
		ω=15t-15t2	вверх	-	-	0,20	3,0	-	0,14	m,ω
		S=0,5t2	Вниз		-	-	1,76		0,20	d,t1
		S=1,5t2	Вниз	-	0,6	0,24	9,9	-	0,10	m,ω
		S=0,9t2	Вниз		-	0,18	-		0,20	P, t1
		φ=10t2	Вниз		-	0,20	1,92	-	0,20	P, t1
		S=t-1,25t2	вверх		-	-	-		0,25	P,d
		φ=8t-20t2	вверх		-	0,20	-	-	0,14	P, ω

 

 

Пример выполнения

Задача 1 (рисунок 1).

Решение 1. Прямолинейное движение (рисунок 1, а). Точка, двигавшаяся равномерно, в некоторый момент времени получила новый закон движения 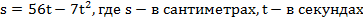, и через некоторый промежуток времени остановилась. Определить все кинематические характеристики движения точки для двух случаев; а) движение по прямолинейной траектории; б) движение по криволинейной траектории постоянного радиуса кривизны r=100см

Рисунок 1 (а).

Закон изменения скорости точки

.

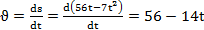Начальную скорость точки найдем из условия:

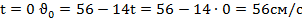
Время торможения до остановки найдем из условия:

при 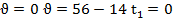, отсюда .

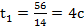Закон движения точки в период равномерного движения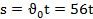

Расстояние, пройденное точкой по траектории за период торможения,

.

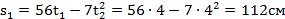Закон изменения касательного ускорения точки

,

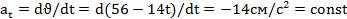откуда следует, что в период торможения точка двигалась равнозамедленно, так как касательное ускорение отрицательно и по значению постоянно.

Нормальное ускорение точки на прямолинейной траектории движения равно нулю, т.е. .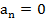

Решение 2. Криволинейное движение (рисунок 1, б).

Рисунок 1 (б)

В этом случае по сравнению со случаем прямолинейного движения остаются без изменения все кинематические характеристики, за исключением нормального ускорения.

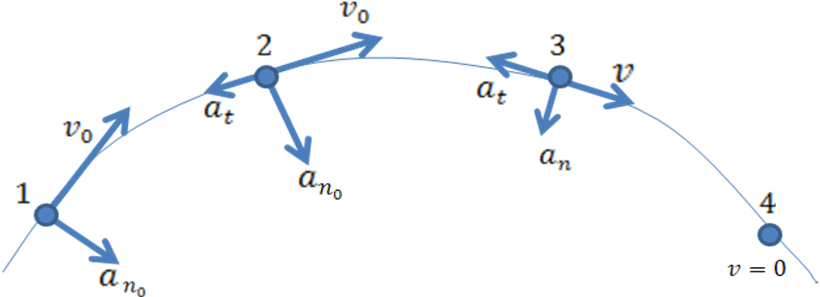
Закон изменения нормального ускорения точки

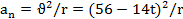
Нормальное ускорение точки в начальный момент торможения

.

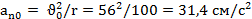Принятая на чертеже нумерация положений точки на траектории: 1 – текущее положение точки в равномерном движении до начала торможения; 2 – положение точки в момент начала торможения; 3 – текущее положение точки в период торможения; 4 – конечное положение точки.

 

Задача 2.

 

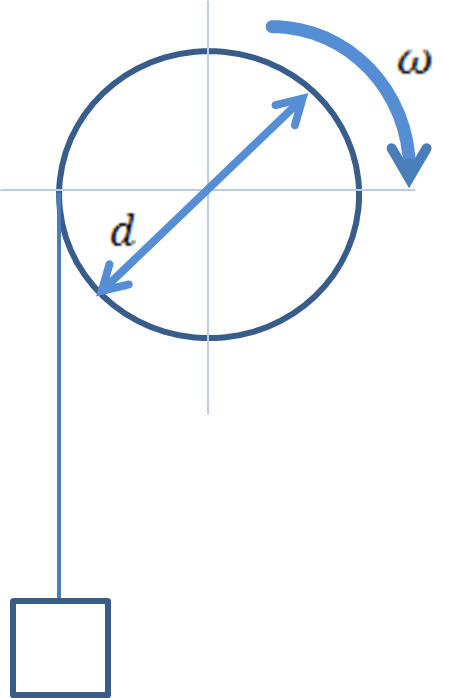
Груз (рис. 2, а) поднимается с помощью барабанной лебедки. Диаметр барабана d=0,3м, а закон его вращения .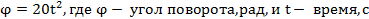

Разгон барабана длился до угловой скорости 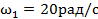. Определить все кинематические характеристики движения барабана и груза.

 

Решение. Закон изменения угловой скорости барабана 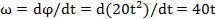. Начальную угловую скорость найдем из условия: 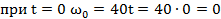; следовательно, разгон начался из состояния покоя. Время разгона найдем из условия: 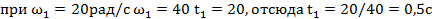. Угол поворота барабана за период разгона .

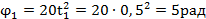Закон изменения углового ускорения барабана 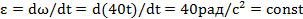, отсюда следует, что в период разгона барабан вращался равноускоренно.

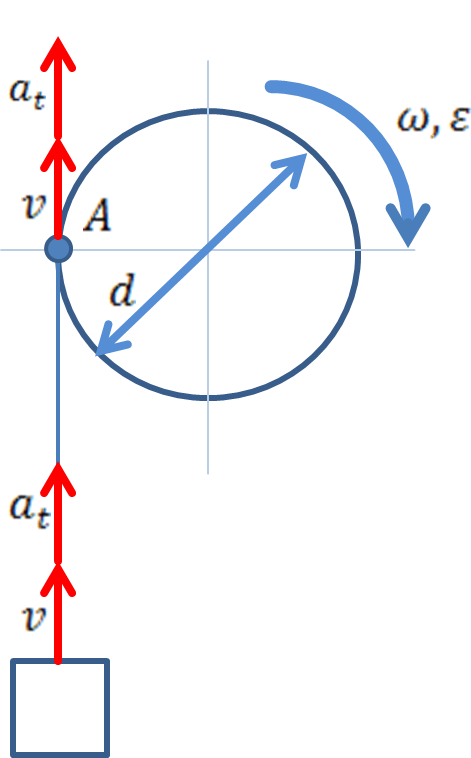
Кинематические характеристики груза равны соответствующим характеристикам любой точки тягового троса, а значит, и точки A, лежащей на ободе барабана (рис. 2, б). Как известно, линейные характеристики точки вращающегося тела определяются через его угловые характеристики.

Расстояние, пройденное грузом за период разгона, 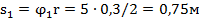. Скорость груза в конце разгона .

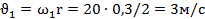Ускорение груза .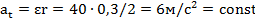

Закон движения груза .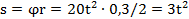

Расстояние, скорость и ускорение груза можно было определить и иначе, через найденный закон движения груза:

.

 

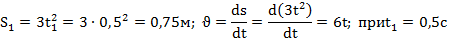
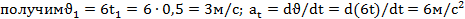Задача 3. Груз, перемещавшийся равномерно вверх по наклонной опорной плоскости, в некоторый момент времени получил торможение в соответствии с новым законом движения 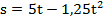, где s – в метрах и t – в секундах. Масса груза m = 100кг, коэффициент трения скольжения между грузом и плоскостью f=0,25. Определить силу F и мощность 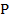на тяговом тросе для двух моментов времени: а) равномерное движение до начала торможения;

б) начальный момент торможения. При расчёте принять g=10 м/ .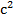

Решение. Определяем кинематические характеристики движения груза.

Закон изменения скорости груза

.

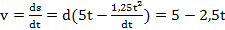Начальная скорость груза (при t=0)

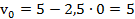м/с.

Ускорение груза

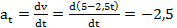м/ 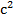=const.

Так как ускорение отрицательно, то движение – замедленное.

1. Равномерное движение груза.

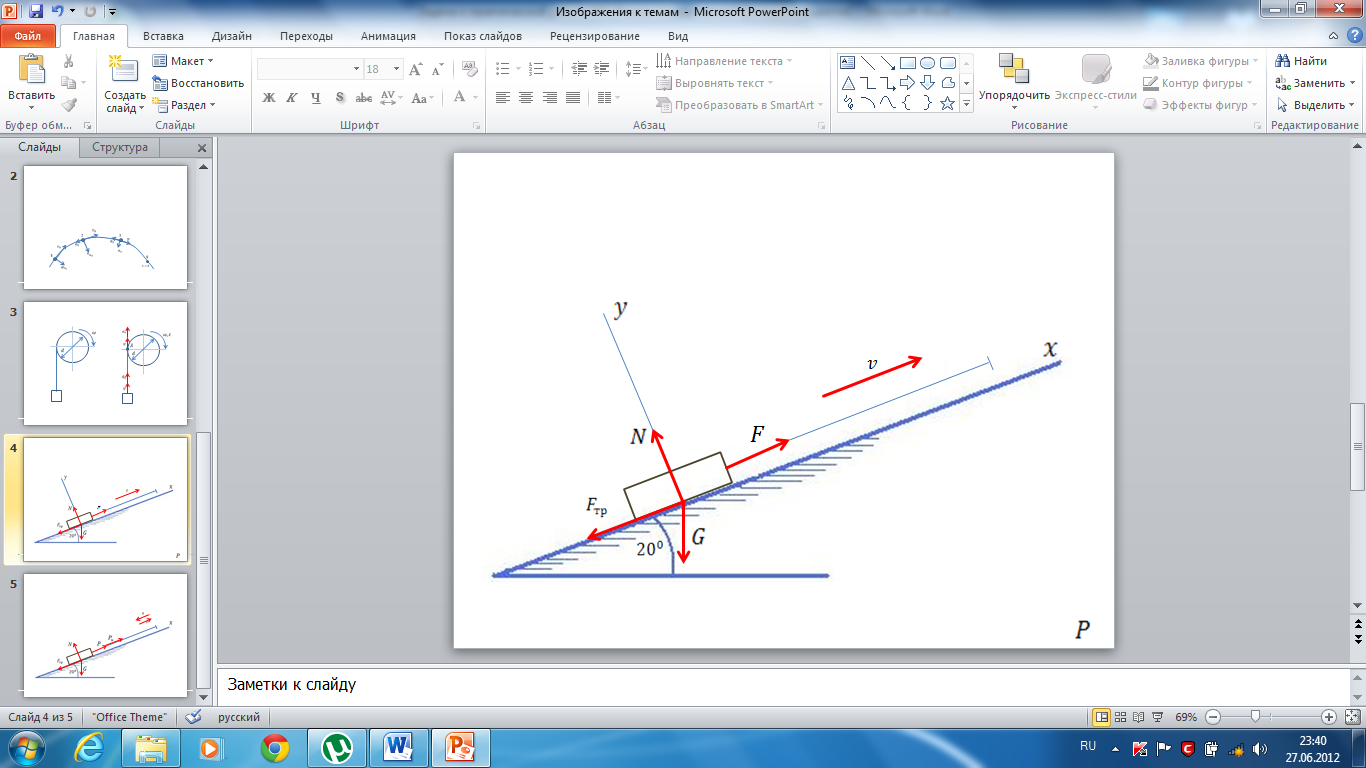
Для определения движущей силы F рассматриваем равновесие груза, на который действует система сходящихся сил: сила на тросе F, сила тяжести груза G=mg, нормальная реакция опорной поверхности N и сила трения 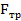, направленная навстречу движению тела. По закону трения, 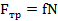. Выбираем направление координатных осей, как показано на чертеже, и составляем два уравнения равновесия для груза:

; ,

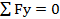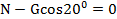отсюда ;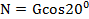

; ,

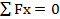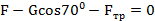отсюда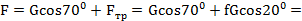

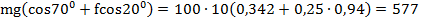H.

Мощность на тросе до начала торможения определим по известной формуле

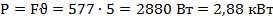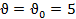, где м/с.

2. Замедленное движение груза.

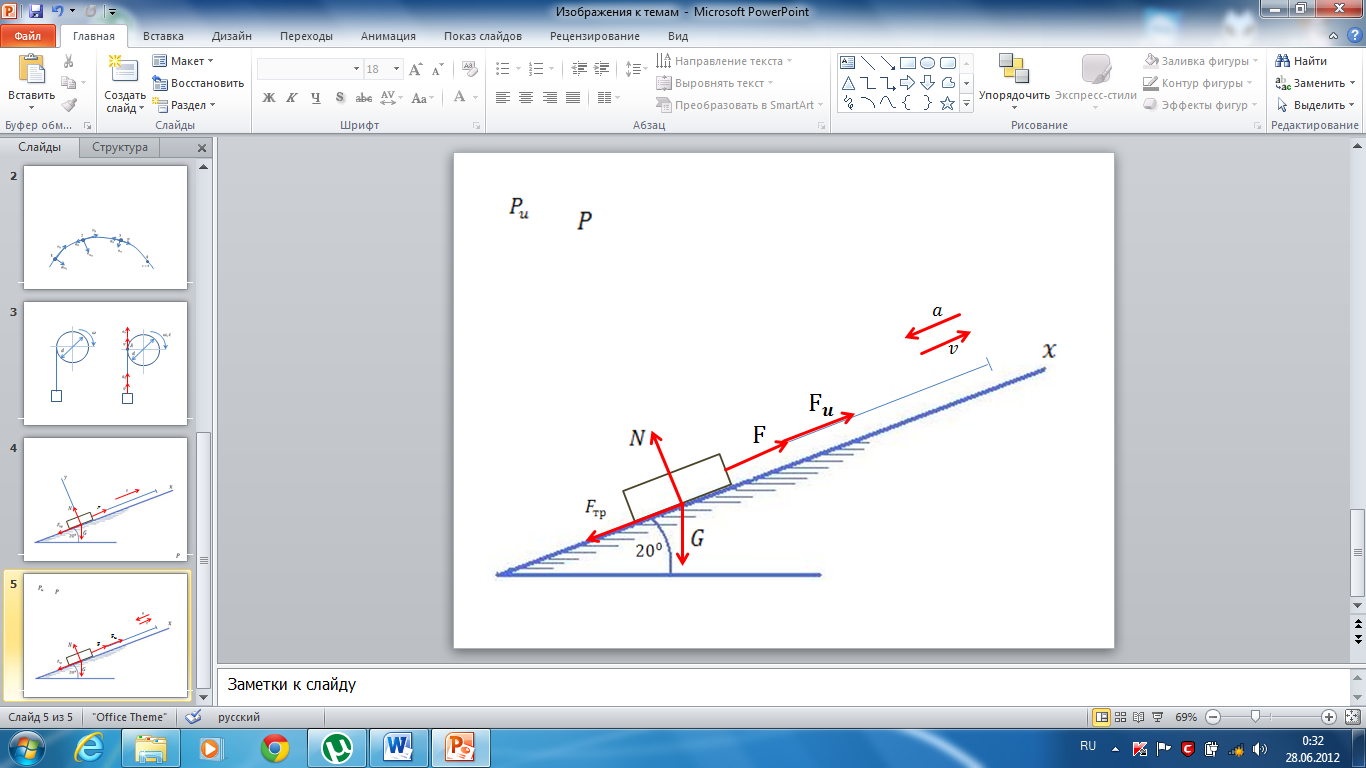
Как известно, при неравномерном поступательном движении тела система действующих на него сил по направлению движения не является уравновешенной. Согласно принципу Даламбера (метод кинетостатики), тело в этом случае можно считать находящимся в условном равновесии, если ко всем действующим на него силам добавить силу инерции 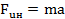, вектор которой направлен противоположно вектору ускорения. Вектор ускорения в нашем случае направлен противоположно вектору скорости, так как груз движется замедленно. Составляем два уравнения равновесия для груза:

;

;

; ,

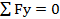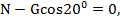
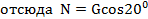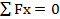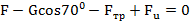отсюда

.

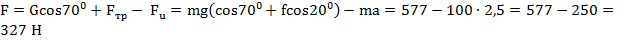Мощность на тросе в момент начала торможения

 

 

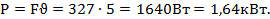
Контрольные вопросы.

1. Как определить численное значение и направление скорости точки в данный момент?

2. Что характеризует нормальная и касательная составляющие полного ускорения?

3. Как перейти от выражения угловой скорости в мин^-1 к ее выражению рад/с?

4. Что называют массой тела? Назовите единицу измерения массы

5. При каком движении материальной точки возникает сила инерции? Чему равно ее численное значение, как она направлена?

6. Сформулируйте принцип Даламбера

7. Возникает ли сила инерции при равномерном криволинейном движении материальной точки?

8. Что такое вращающий момент?

9. Как выражается зависимость между вращающим моментом и угловой скорости при данной передаваемой мощности?

10. Основное уравнение динамики для вращательного движения.

 

Практическая работа №7

«Расчет конструкций на прочность»

Цель работы: определять прочность, размеры сечения и допускаемую нагрузку

Теоретическое обоснование.

Зная силовые факторы и геометрические характеристики сечения при деформации растяжение (сжатие), мы можем определить напряжение по формулам. А что бы понять, выдержит ли наша деталь (вал, шестерня и т. д.) внешнюю нагрузку. Необходимо эту величину сравнить с допустимым напряжением.

Итак, уравнение статической прочности

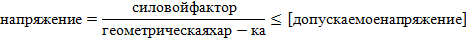
На его основании решают 3 типа задач:

1) проверка прочности

2) определение размеров сечения

3) определение допускаемой нагрузки

Итак, уравнение статической жёсткости

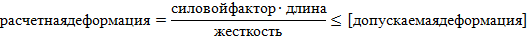
На его основании решают также 3 типа задач

Уравнение статической прочности при растяжении (сжатии)

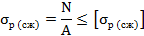
1) Первый тип - проверка прочности

,

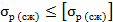т. е. решаем левую часть и сравниваем с допускаемым напряжением.

2) Второй тип - определение размеров сечения

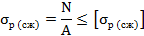
из правой части площадь поперечного сечения

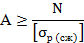
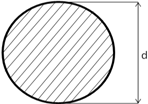Сечение круг

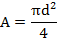
отсюда диаметр d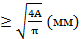

Сечение прямоугольник

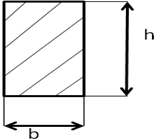
A = bh

 

 

Сечение квадрат

 

 

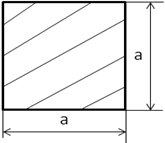
A = a² (мм²)

 

 

Сечение полукруг

 

 

 

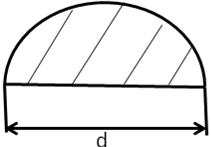
A=0,5 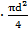(мм²)

 

 

Сечения швеллер, двутавр, уголок и т. д.

Значения площади — из таблицы, принимается по ГОСТ

 

 

3) Третий тип - определение допустимой нагрузки;

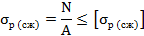
Из правой части допускаемая нагрузка

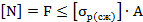
принимается в меньшую сторону, целое число

ЗАДАНИЕ

Задача

А) Проверка прочности (проверочный расчет)

Для заданного бруса построить эпюру продольных сил и проверить прочность на обоих участках. Для материала бруса (сталь Ст3) принять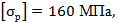

 

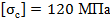
№ варианта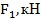
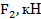
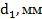
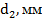
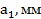
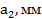
	12,5	5,3	-			-
		2,3			-	-
		4,2		-	-

 

Б) Подбор сечения (проектный расчет)

Для заданного бруса построить эпюру продольных сил и определить размеры поперечного сечения на обоих участках. Для материала бруса (сталь Ст3) принять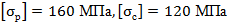

 

№ варианта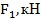
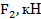
	1,9	2,5
	2,8	1,9
	3,2

 

В) Определение допускаемой продольной силы

Для заданного бруса определить допускаемые значения нагрузок 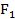и ,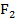

построить эпюру продольных сил. Для материала бруса (сталь Ст3) принять 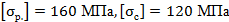. При решении задачи считать, что на обоих участках бруса вид нагружения одинаков.

№ варианта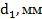
	-	-
			-	-
	-	-

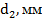
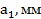
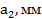
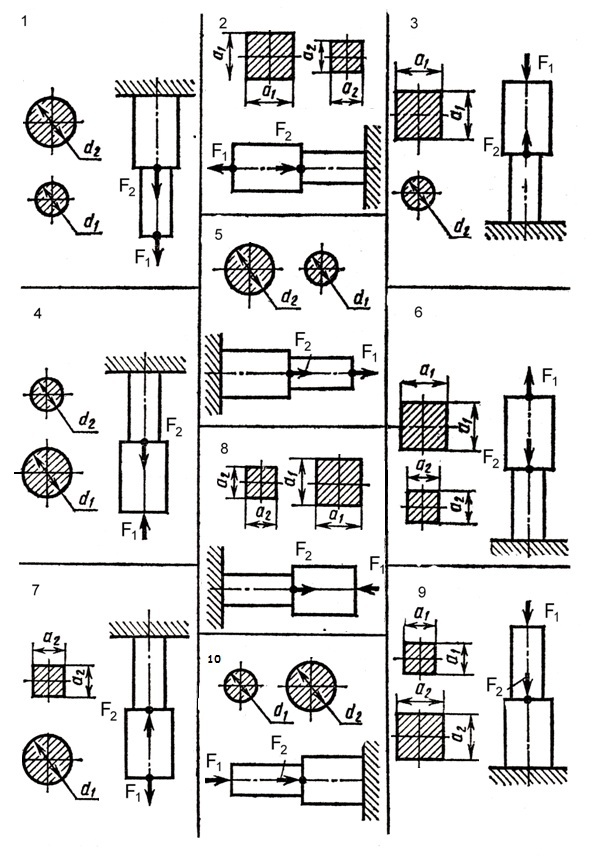
Пример выполнения задания

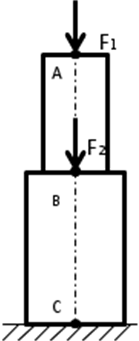
Задача 1 (рисунок 1).

Проверить прочность колонны, выполненной из двутавровых профилей заданного размера. Для материала колонны (сталь Ст3) принять допускаемые напряжения при растяжении 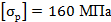и при сжатии 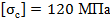. В случае наличия перезагрузки или значительной недогрузки подобрать размеры двутавров, обеспечивающие оптимальную прочность колонны.

 

 

Решение.

Заданный брус имеет два участка 1, 2. Границами участков являются сечения, в которых приложены внешние силы. Так как силы, нагружающие брус, расположены по его центральной продольной оси, то в поперечных сечениях возникает лишь один внутренний силовой фактор – продольная сила 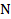, т.е. имеет место растяжение (сжатие) бруса.

 

 

Для определения продольной силы применяем метод сечений метод сечений. Проводя мысленно сечение в пределах каждого из участков, будем отбрасывать нижнюю закрепленную часть бруса и оставлять для рассмотрения верхнюю часть. На участке 1 продольная сила постоянна и равна

.

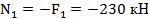На участке 2 продольная сила также постоянна и равна

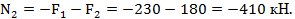
Знак минус указывает на то, что на обоих участках брус сжат.

Строим эпюру продольных сил 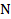. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, откладываем перпендикулярно ей в произвольном масштабе полученные значения 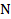. Как видим, эпюра оказалась очерчена прямыми линиями, параллельными базовой.

Выполняем проверку прочности бруса, т.е. определяем расчетное напряжение (для каждого участка в отдельности) и сравниваем его с допускаемым. Для этого используем условие прочности при сжатии

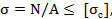
где площадь 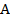является геометрической характеристикой прочности поперечного сечения. Из таблицы прокатной стали берем:

 

для двутавра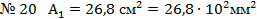
для двутавра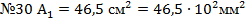

Проверка прочности:

 

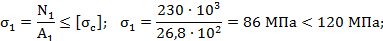
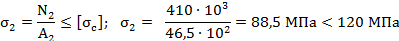Значения продольных сил взяты по абсолютной величине.

Прочность бруса обеспечена, однако имеет место значительная (более 25%) недогрузка, что недопустимо вследствие перерасхода материала.

Из условия прочности определяем новые размеры двутавра для каждого из участков бруса:
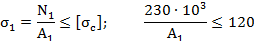Отсюда требуемая площадь

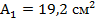
По таблице ГОСТа выбираем двутавр № 16, для которого ;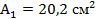

Отсюда требуемая площадь

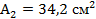
По таблице ГОСТа выбираем двутавр №24, для которого ;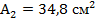

При выбранных размерах двутавров также имеет место недогрузка, однако незначительная (менее 5%)

 

Задача №2.

Для бруса с заданными размерами поперечного сечения определить допускаемые значения нагрузок 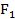и 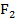. Для материала бруса (сталь Ст3) принять допускаемые напряжения при растяжении 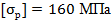и при сжатии .

 

 

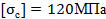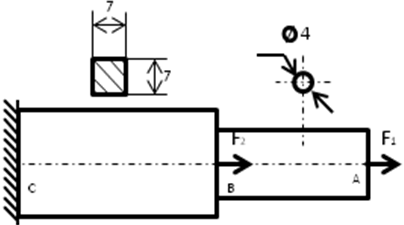
Решение.

Заданный брус имеет два участка 1, 2. Имеет место растяжение (сжатие) бруса.

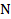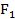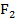Применяя метод сечений, определяем продольную силу , выражая ее через искомые силы и . Проводя в пределах каждого из участков сечение, будем отбрасывать левую часть бруса и оставлять для рассмотрения правую часть. На участке 1 продольная сила постоянна и равна

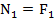
На участке 2 продольная сила также постоянна и равна

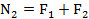
Знак плюс указывает на то, что на обоих участкахбрус растянут.

Строим эпюру продольных сил 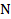. Эпюра очерчена прямыми линиями, параллельными базовой.

 

 

Из условия прочности при растяжении определяем допускаемые значения нагрузок 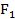и 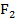предварительно вычислив площади заданных поперечных сечений:

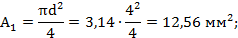
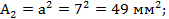
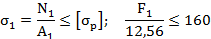
Отсюда ;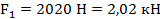

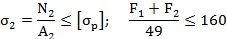
Отсюда

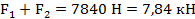
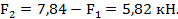
Контрольные вопросы.

1. Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?

2. Запишите условие прочности при растяжении и сжатии.

3. Как назначают знаки продольной силы и нормального напряжения?

4. Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?

5. Различаются ли условия прочности при расчете на растяжение и расчете на сжатие?

6. В каких единицах измеряется напряжение?

7. Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов?

8. В чем разница между предельным и допускаемым напряжением?

 

Практическая работа №8

«Решение задач по определению главных центральных моментов инерции плоских геометрических фигур»

Цель работы: определить аналитическим путем моменты инерции плоских тел сложной формы

Теоретическое обоснование. Координаты центра тяжести сечения можно выразить через статический момент:

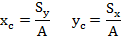
где относительно оси Оx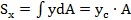

относительно оси Оy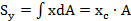

Статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние ее центра тяжести до этой оси. Статический момент имеет размерность 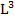. Статический момент может быть величиной положительной, отрицательной и равен нулю (относительно любой центральной оси).

Осевым моментом инерции сечения называется взятая по всему сечению сумма произведений или интеграл элементарных площадок на квадраты их расстояний до некоторой оси, лежащей в плоскости рассматриваемого сечения

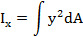
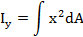
Осевой момент инерции выражается в единицах - 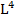. Осевой момент инерции- величина всегда положительная и не равна нулю.

Оси, проходящие через центр тяжести фигуры, называются центральными. Момент инерции относительно центральной оси называется центральным моментом инерции.

Момент инерции относительно какой-либо оси равен центра