Идея ДП представляется так: большую N-мерную задачу, разбиваем на n задач, каждую из которых называют этапом.
Для каждой одномерной задачи ищется оптимальное решение, с учетом оптимального решения, полученного для уже решенных задач.
Решение последней одномерной задачи дает оптимальное решение всей n-мерной задачи.
Вычисление динамического программирования производится рекуррентно, т.е. решение первой задачи является начальным условием для другой задачи.
Способ выполнения рекуррентных вычислений зависит от того как выполняется декомпозиция исходной задачи.
Как правило подзадачи связаны между собой хотя бы одним ограничением или условием.
Рекуррентные вычисления динамического программирования могут выполняться либо от начала задачи к последней, либо от последней задачи к начальной.
d(Xj,Xi) – расстояние между j и i узлом.
fi(Xi) – кратчайшее расстояние до вершины Xi на этапе с номером i.
fi(Xi) = min{d(Xi-1,Xi)+fi-1(Xi-1)}, i = 1,2,3…
Для того чтобы поставить задачу ДП необходимо определить элементы этой задачи:
1) определить этапы, т.е. определить их количество и содержание
2) определение для каждого этапа множества вариантов решения
3) определение состояния на каждом этапе
Этапы в задачах могут быть выделены естественным образом, когда есть указания о последовательности действий или о периодах времени или искусственным образом, когда части задачи можно рассматривать отдельно.
Задача о загрузке. Пример
Задача о рациональной загрузке т/с с ограничением по вместимости или грузоподъемности
Для каждой единицы груза каждого вида указывается масса или объем, а также указывается приносимая прибыль или полученный эффект.
Задача состоит в определении загрузки т/с таким набором грузов, которые приносят наибольшую прибыль или наибольший эффект.
Этапы:
1) В качестве i этапа возьмем загрузку i-го рассмотрения
2) Варианты решения: количество единиц i-го груза
В качестве состояния Xi возьмем суммарный вес грузов, решения о погрузке которых приняты на этапах с i до n для метода обратной прогонки.
fi(Xi) – максимальная суммарная прибыль от этапов i, i+1,..n при заданном состоянии Xi на i этапе.
fi(Xi) = max {rimi + fi+1(Xi+1)}= max{rimi + fi+1(xi-Wmi)}
Wi – масса i-го вида груза
W – общая грузоподъемность т/с.
Пример – задача о загрузке самолета.
35.Задача планирования рабочей силы. Пример
При выполнение некоторых проектов число рабочих, необходимые для выполнения какого-либо проекта, регулируется путем их найма и увольнения. Так как наем и увольнение рабочих связано с дополнительными затратами нужно определить как должна регулир. Численность рабочих для реализации проекта. Этапы:
Этап i- порядковый номер недели.
Вариантами решений на этапе-xi-1-кол-во раб-щих на i-ой неделе.
Функция управления на этапе- u(xi)=C1(xi-bi)+C2(xi –xi-1).
Реккурентное уравнение-fi(xi-1)=min{ C1(xi-bi)+C2(xi –xi-1)+fi+1(x1)},i=1,2…n. Вычисления начинаются с этапа n при xn=bn.
Задача замены оборудования. Пример
старое оборудование изнашивается и расходы на эксплуатацию могут превысить расходы на покупку нового.
Задача замены оборудования сводится к определению оптимального срока эксплуатации механизма. Этапы:
Этап I представляется номером года.
Вариантами решения на i-ом этапе является продолжительность эксплуатации или замена механизма в начале года.
Состоянием на i-ом этапе является срок экспл. T
Функция управления-u(t)=r(t)-c(t)
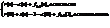 Реккурентное уравнение-
Реккурентное уравнение-
fi(t)-max
Пример – задача про газонокосилку.
Вероятностное ДП. Азартная игра
рассматриваем с последнего этапа,
исход вращения | fi(j)| прекратить | Вращать | решение
Обобщенная модель управления запасами.
Запасы необходимы для обеспечения непрерывности производственного процесса.
Стратегия управления запасами должна отвечать на 2 вопроса:
1) какое количество запасов заказывать
2) когда заказывать
Суммарные затраты…
Система управления запасами может быть непрерывной и периодической.



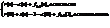 Реккурентное уравнение-
Реккурентное уравнение-


