Рассмотрим мембрану, имеющую в состоянии покоя форму прямоугольника, ограниченного прямыми x=0, x=l, y=0, y=m.
Уравнение колебаний мембраны
 (107)
(107)
Начальные условия
 (108)
(108)
 (109)
(109)
Граничные условия
 (110)
(110)
Будем решать задачу методом Фурье. Для этого будем искать решение в виде произведения трех функций, каждая из которых зависит только от одного аргумента:
 (111)
(111)
 (1)
(1)
 (2)
(2)

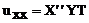

Из граничных условий следует, что
X(0)=0, X(l)=0, Y(0)=0, Y(m)=0 (112)
Подставляя (111) в (107), получим

Разделим на XYT

 (3)
(3)
 (4)
(4)
Анализируя последнее равенство, заключаем

 ,
,  (113)
(113)
В результате, для функции X(x) получаем
 ,
,  (114)
(114)
Для функции Y(y)
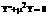 , Y(0)=Y(m)=0 (115)
, Y(0)=Y(m)=0 (115)
Из (1) и (2) à X(0)=0, X(l)=0
Из (3) и (4) à Y(0)=0, Y(m)=0
Для функции T(t)
 (116)
(116)
Решение (114) имеет вид
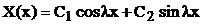 (117)
(117)
Решение 3.5 имеет вид
 (118)
(118)
Из краевого условия X(0)=X(l)=0 находим  = 0 и
= 0 и
 , где k – целое число
, где k – целое число
Аналогично, из Y(0)=Y(m)=0 находим 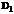 = 0 и
= 0 и
 , где n – целое число
, где n – целое число
В результате получаем собственные числа и собственные функции
 (119)
(119)
 (120)
(120)
Уравнение для функции T(t) принимает вид:
 (121)
(121)
Решение этого уравнения, зависящее от двух параметров k и n, имеет вид:
 (122)
(122)
Здесь
 (123)
(123)
- собственные частоты колебаний мембраны
Таким образом, частное решение уравнения колебаний прямоугольной мембраны имеет вид
 (124)
(124)
Оно может быть приведено к виду



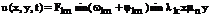 (125)
(125)
Где  ,
, 
Отсюда видно, что каждая точка мембраны с координатами (x,y) совершает простое гармоническое колебание с частотой  и амплитудой
и амплитудой  . Все точки колеблются в одной фазе. Точки, координаты которых удовлетворяют уравнениям
. Все точки колеблются в одной фазе. Точки, координаты которых удовлетворяют уравнениям
 ,
, 
будут колебаться с наибольшей амплитудой называются пучностями. Линии, точки которых не колеблются (амплитуда равна нулю), называются узловыми линиями.
Общее решение нашей задачи о колебаниях мембраны представляется как сумма частных
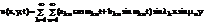 (126)
(126)
Неизвестные коэффициенты a и b ищутся из начальных условий:
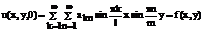 (127)
(127)
 (128)
(128)
Формулы (127) и (128) представляют собой разложение функции двух переменных в двойной ряд Фурье. Коэффициенты этого разложения находятся аналогично коэффициентам однократного ряда и имеют вид
 (129)
(129)
 (130)
(130)
Колебания круглой мембраны.
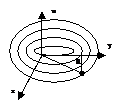
Применим метод решения задачи о колебаниях прямоугольной мембраны к колебаниям круглой мембраны. Пусть мембрана в состоянии покоя занимает круг радиуса R с центром в начале координат. Введем полярные координаты r и φ:
x=rcos φ, y=rsin φ.
Выполняя замену переменных u(x,y,t) à u(r,φ,t) уравнение колебаний мембраны приводятся к виду
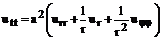 (131)
(131)
Граничные условие будет иметь вид
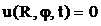
Начальные условия
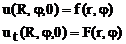
Будем рассматривать только осесимметричные колебания мембраны, т.е. начальные условия не должны зависеть от угла φ. Очевидно, что в любой момент времени скорости и отклонения точек будут зависеть от угла, поэтому наша задача упрощается:
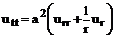 (132)
(132)
Граничные условия
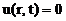
Начальные условия
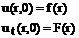
Будем искать решение в виде
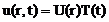 (133)
(133)
Из краевого условия сразу находим
U(R)=0
Подставляя (133) в уравнение, получаем
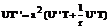 разделим на UT
разделим на UT 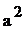
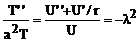 (134)
(134)
В результате приходим к уравнениям
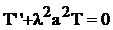 (135)
(135)
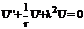 (136)
(136)
В последнем сделаем замену 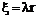 :
:
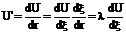
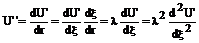
Подставляя в наше уравнение, получаем
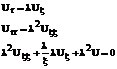
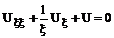 (137)
(137)
Получившееся уравнение является частным случаем уравнения Бесселя:
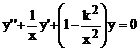 (138)
(138)
Решениями последнего уравнения при заданном k называется бесселевыми функциями порядка k (цилиндрическими функциями).
Найдем решение уравнения (138). Очевидно, что оно имеет особую точку при x=0, поэтому его решение будем искать в виде степенного ряда. Для этого преобразуем его к виду:
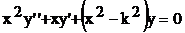 (139)
(139)
Записываем ряд:
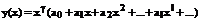 (140)
(140)
Подставляя (140) в (139) и приравнивая коэффициенты при каждой степени x нулю, получим систему уравнений
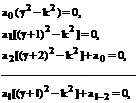 (141)
(141)
Где l=2,3…
Предполагая, что 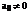 , находим
, находим
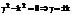
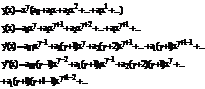
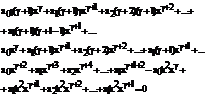
Из второго уравнения (141) находим, что 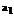 =0. преобразуем l-е уравнение в системе (141).
=0. преобразуем l-е уравнение в системе (141).

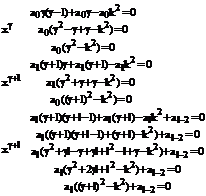
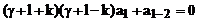 (142)
(142)
Отсюда получаем рекуррентную формулу:
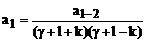 (143)
(143)
С учетом найденного 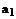 =0 делаем вывод, что все нечетные коэффициенты равны нулю. Очевидно, что при
=0 делаем вывод, что все нечетные коэффициенты равны нулю. Очевидно, что при 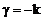 решение обращается в бесконечность при x=0. будем рассматривать случай
решение обращается в бесконечность при x=0. будем рассматривать случай 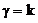 . В результате, для четных коэффициентов получаем
. В результате, для четных коэффициентов получаем
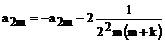 (144)
(144)
Применяя эту формулу m-1 раз, получим
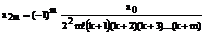 (145)
(145)
Полагая,
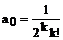
Получаем
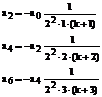
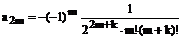 (146)
(146)
В результате, полученное решение 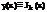 называется функцией Бесселя первого рода k-ого порядка и имеет вид:
называется функцией Бесселя первого рода k-ого порядка и имеет вид:
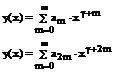
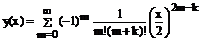 (147)
(147)



 (107)
(107) (108)
(108) (109)
(109) (110)
(110) (111)
(111) (1)
(1) (2)
(2)
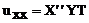



 (3)
(3) (4)
(4)
 ,
,  (113)
(113) ,
,  (114)
(114)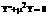 , Y(0)=Y(m)=0 (115)
, Y(0)=Y(m)=0 (115) (116)
(116)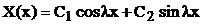 (117)
(117) (118)
(118) = 0 и
= 0 и , где k – целое число
, где k – целое число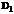 = 0 и
= 0 и , где n – целое число
, где n – целое число (119)
(119) (120)
(120) (121)
(121) (122)
(122) (123)
(123) (124)
(124)


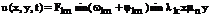 (125)
(125) ,
, 
 и амплитудой
и амплитудой  . Все точки колеблются в одной фазе. Точки, координаты которых удовлетворяют уравнениям
. Все точки колеблются в одной фазе. Точки, координаты которых удовлетворяют уравнениям ,
, 
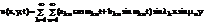 (126)
(126)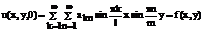 (127)
(127) (128)
(128) (129)
(129) (130)
(130)
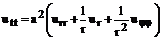 (131)
(131)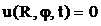
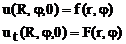
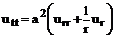 (132)
(132)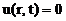
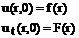
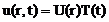 (133)
(133)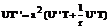 разделим на UT
разделим на UT 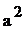
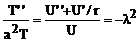 (134)
(134)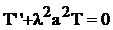 (135)
(135)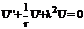 (136)
(136)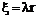 :
: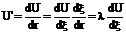
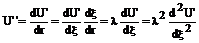
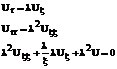
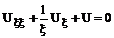 (137)
(137)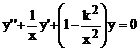 (138)
(138)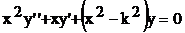 (139)
(139)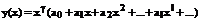 (140)
(140)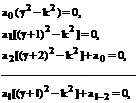 (141)
(141)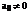 , находим
, находим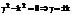
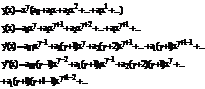
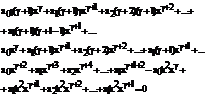
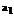 =0. преобразуем l-е уравнение в системе (141).
=0. преобразуем l-е уравнение в системе (141).
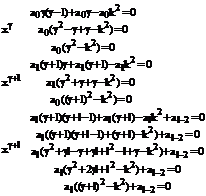
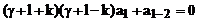 (142)
(142)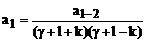 (143)
(143)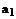 =0 делаем вывод, что все нечетные коэффициенты равны нулю. Очевидно, что при
=0 делаем вывод, что все нечетные коэффициенты равны нулю. Очевидно, что при 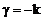 решение обращается в бесконечность при x=0. будем рассматривать случай
решение обращается в бесконечность при x=0. будем рассматривать случай 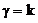 . В результате, для четных коэффициентов получаем
. В результате, для четных коэффициентов получаем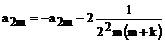 (144)
(144)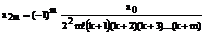 (145)
(145)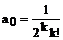
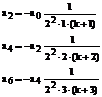
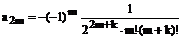 (146)
(146)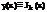 называется функцией Бесселя первого рода k-ого порядка и имеет вид:
называется функцией Бесселя первого рода k-ого порядка и имеет вид: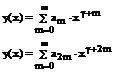
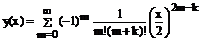 (147)
(147)


