Определение 1.6.1. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае она называется вырожденной.
Теорема 1.6.1. Определитель произведения матриц равен произведению определителей. Для двух матриц: 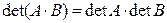 .
.
Следствие 1.6.1. Произведение любых невырожденных матриц само будет невырожденной матрицей.
Определение 1.6.2. Обратной к квадратной матрице  называется матрица
называется матрица  , которая удовлетворяет условию
, которая удовлетворяет условию
 .(1.6.1)
.(1.6.1)
Теорема 1. 6.2. Матрица A тогда и только тогда имеет обратную матрицу, когда она невырожденная.
Доказательство.
Необходимость. Пусть матрица A имеет обратную матрицу  , тогда
, тогда  и
и  . По теореме 1.6.1
. По теореме 1.6.1  . Так как
. Так как  , имеем
, имеем 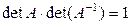 . Значит
. Значит  и
и  , т. е. матрицы A и
, т. е. матрицы A и  невырожденные, а
невырожденные, а 
Достаточность. Для матрицы  ;
;  , составим матрицу из алгебраических дополнений и затем транспонируем ее. Получившуюся в результате матрицу обозначим
, составим матрицу из алгебраических дополнений и затем транспонируем ее. Получившуюся в результате матрицу обозначим  и назовем присоединенной (или союзной) к A. Иными словами,
и назовем присоединенной (или союзной) к A. Иными словами,

где 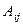 – алгебраическое дополнениеэлемента
– алгебраическое дополнениеэлемента 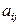 .
.
Вычисляя произведения  и
и  матриц, с учетом теоремы 1.3.1 получим
матриц, с учетом теоремы 1.3.1 получим
 .
.
Разделив последнее соотношение на величину 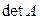 , имеем:
, имеем:

откуда c учетом равенств (1.6.1), (1.2.4), найдем:  . Мы получили формулу нахождения обратной матрицы и, следовательно, доказали ее существование.
. Мы получили формулу нахождения обратной матрицы и, следовательно, доказали ее существование.
Таким образом, формула для вычисления обратной матрицы имеет вид:
 (1.6.2)
(1.6.2)
Замечание 1.6.1. Для каждой невырожденной матрицы А существует единственная обратная матрица  .
.
Пример 1.6.1.
Дано

Найти  .
.
Решение.


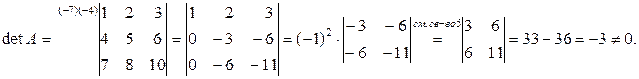
Следовательно, матрица А невырожденная и  существует.
существует.
Найдем алгебраические дополнения  элементов данной матрицы:
элементов данной матрицы:









Подставляя полученное в формулу (1.6.2), находим

Проверка:
 .
.
Замечание 1.6.1. Существует еще один способ нахождения обратной матрицы при помощи элементарных преобразований. Этот способ состоит в следующем: составляется матрица размера  , при помощи приписывания к матрице A справа единичной матрицы. Элементарными преобразованиями строк преобразуют полученную матрицу так, чтобы обратить ее левую половину в единичную матрицу. Тогда справа получится матрица
, при помощи приписывания к матрице A справа единичной матрицы. Элементарными преобразованиями строк преобразуют полученную матрицу так, чтобы обратить ее левую половину в единичную матрицу. Тогда справа получится матрица  .
.
Пример 1.6.2. Для матрицы из примера 1.6.1 найти обратную матрицу при помощи элементарных преобразований.
Решение.


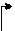



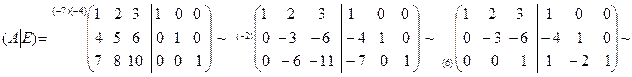


Свойства обратных матриц:
1.  .
.
Непосредственно следует из равенства 1.6.1.
2.  .
.
Доказательство.
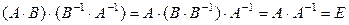 . Следовательно, матрицы
. Следовательно, матрицы  и
и 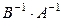 обратные по отношению друг к другу, т. е.
обратные по отношению друг к другу, т. е.  .
.
3.  .
.
Доказательство.
Из соотношения 1.6.1:  . По свойству 4 операции транспонирования (см. §2)
. По свойству 4 операции транспонирования (см. §2)  . Следовательно, матрицы
. Следовательно, матрицы  и
и  взаимообратные, т. е.
взаимообратные, т. е.  .
.
Определение 1.6.2. Простейшими матричными уравнениями будем называть уравнения следующих трех типов:
 ,
,  ,
, 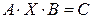 , (1.6.3)
, (1.6.3)
где 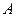 ,
,  ,
,  – некоторые числовые матрицы, а
– некоторые числовые матрицы, а  – неизвестная матрица, которую нужно найти.
– неизвестная матрица, которую нужно найти.
Под решением матричного уравнения будем понимать матрицу X, которая обращает матричное уравнение в тождество.
Искать решение матричных уравнений будем с помощью обратных матриц в зависимости от типа уравнения следующими тремя способами:
1) Если  , то домножая обе части уравнения
, то домножая обе части уравнения  на
на  слева, получим
слева, получим  .
.
2) Если  , то домножая обе части уравнения
, то домножая обе части уравнения  на
на  справа, получим
справа, получим  .
.
3) Если  и
и  , то домножая уравнение
, то домножая уравнение 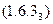 на
на  слева и на
слева и на  справа, получим
справа, получим
 .
.
Пример 1.6.3. Решить матричные уравнения:
a)  b)
b)  c)
c) 
Решение:
a)Матричное уравнение можно переписать в виде:  , где
, где

Получили уравнение вида (1.6.  ), решение которого – матрица
), решение которого – матрица  .
.
Найдем матрицу  :
:
 существует;
существует;
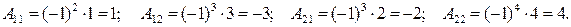

Таким образом,
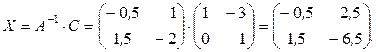
b) Матричное уравнение можно переписать в виде:  , где
, где

Получили уравнение вида (1.6.  ), решение которого ищется в виде:
), решение которого ищется в виде:  . Найдем матрицу
. Найдем матрицу  :
:
 существует;
существует;



c) Матричное уравнение можно переписать в виде (1.6.  ):
):  , где
, где

Решение данного уравнения ищется в виде:  . Найдем матрицы
. Найдем матрицы  и
и  :
:

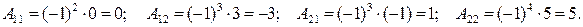

 существует;
существует;

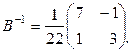
Окончательно, находим

Замечание 1.6.2. В случае, когда 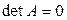 и
и  , приведенные способы решений применять нельзя. В этом случае неизвестную матрицу X находят, сводя матричное уравнение к системе линейных уравнений.
, приведенные способы решений применять нельзя. В этом случае неизвестную матрицу X находят, сводя матричное уравнение к системе линейных уравнений.
Пример 1.6.4. Решить матричное уравнение:

Решение:
Так как  , то решать матричное уравнение с помощью обратной матрицы нельзя. Пусть матрица X состоит из элементов
, то решать матричное уравнение с помощью обратной матрицы нельзя. Пусть матрица X состоит из элементов  , тогда по правилу умножения матриц (1.2.3) имеем:
, тогда по правилу умножения матриц (1.2.3) имеем:

Используя определение 1.1.2 равенства матриц, составим систему:

Таким образом, матрица X имеет вид: 
 .
.
Замечание 1.6.3. Более подробно решение систем линейных уравнений мы будем рассматривать в следующей главе.
* Пьер Ф. Саррюс (1798–1858) – французский математик. В 1833 году сформулировал правило для вычисления определителя 3-го порядка, основанное на приписывании к матрице определителя строк или столбцов.



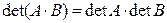 .
.  называется матрица
называется матрица  , которая удовлетворяет условию
, которая удовлетворяет условию .(1.6.1)
.(1.6.1) и
и  . По теореме 1.6.1
. По теореме 1.6.1  . Так как
. Так как  , имеем
, имеем 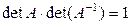 . Значит
. Значит  и
и  , т. е. матрицы A и
, т. е. матрицы A и 
 ;
;  и назовем присоединенной (или союзной) к A. Иными словами,
и назовем присоединенной (или союзной) к A. Иными словами,
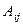 – алгебраическое дополнениеэлемента
– алгебраическое дополнениеэлемента 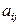 .
. и
и  матриц, с учетом теоремы 1.3.1 получим
матриц, с учетом теоремы 1.3.1 получим .
.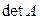 , имеем:
, имеем:
 . Мы получили формулу нахождения обратной матрицы и, следовательно, доказали ее существование.
. Мы получили формулу нахождения обратной матрицы и, следовательно, доказали ее существование. (1.6.2)
(1.6.2)


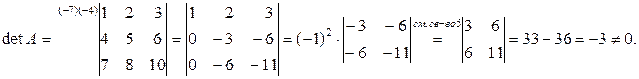
 элементов данной матрицы:
элементов данной матрицы:









 .
. , при помощи приписывания к матрице A справа единичной матрицы. Элементарными преобразованиями строк преобразуют полученную матрицу так, чтобы обратить ее левую половину в единичную матрицу. Тогда справа получится матрица
, при помощи приписывания к матрице A справа единичной матрицы. Элементарными преобразованиями строк преобразуют полученную матрицу так, чтобы обратить ее левую половину в единичную матрицу. Тогда справа получится матрица 



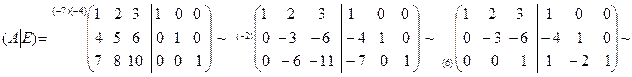



 .
.  .
. 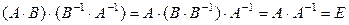 . Следовательно, матрицы
. Следовательно, матрицы  и
и 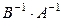 обратные по отношению друг к другу, т. е.
обратные по отношению друг к другу, т. е.  .
. . По свойству 4 операции транспонирования (см. §2)
. По свойству 4 операции транспонирования (см. §2)  . Следовательно, матрицы
. Следовательно, матрицы  и
и  взаимообратные, т. е.
взаимообратные, т. е.  .
.  ,
,  ,
, 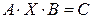 , (1.6.3)
, (1.6.3)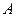 ,
,  ,
,  – некоторые числовые матрицы, а
– некоторые числовые матрицы, а  – неизвестная матрица, которую нужно найти.
– неизвестная матрица, которую нужно найти. на
на  .
. на
на  .
. , то домножая уравнение
, то домножая уравнение 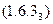 на
на  справа, получим
справа, получим .
. b)
b)  c)
c) 
 , где
, где
 ), решение которого – матрица
), решение которого – матрица  существует;
существует;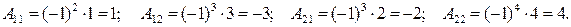

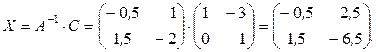
 , где
, где
 ), решение которого ищется в виде:
), решение которого ищется в виде:  . Найдем матрицу
. Найдем матрицу  существует;
существует;


 ):
):  , где
, где
 :
:
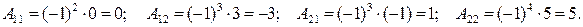

 существует;
существует;
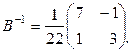

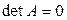 и
и  , приведенные способы решений применять нельзя. В этом случае неизвестную матрицу X находят, сводя матричное уравнение к системе линейных уравнений.
, приведенные способы решений применять нельзя. В этом случае неизвестную матрицу X находят, сводя матричное уравнение к системе линейных уравнений.
 , то решать матричное уравнение с помощью обратной матрицы нельзя. Пусть матрица X состоит из элементов
, то решать матричное уравнение с помощью обратной матрицы нельзя. Пусть матрица X состоит из элементов  , тогда по правилу умножения матриц (1.2.3) имеем:
, тогда по правилу умножения матриц (1.2.3) имеем:


 .
.


