Рассмотрим ОЗЛП, где базисные переменные  разрешены относительно свободных
разрешены относительно свободных  . Например,
. Например,




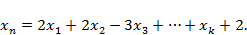
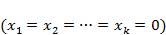 – вершина, при этом базисные переменные
– вершина, при этом базисные переменные  ,
,  ,
,  .
.
В ОЗЛП все переменные должны быть 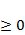 , следовательно, эта вершина недопустима. Признаком недопустимости вершины является наличие отрицательных свободных членов в ограничениях равенствах. Если отрицательный свободный член есть, то надо перейти в другую вершину, для чего одну базисную переменную сделать свободной и приравнять к нулю, а какую-то свободную превратить в базисную. Следовательно, переход из одной вершины в другую осуществляется путем замены базисной переменной на свободную. Это называется симплекс-преобразованием. Если мы будем переходить из вершины в вершину «в сторону ОДР», то за конечное число таких переходов попадем в допустимую вершину. Назовем ее опорной вершиной, а соответствующее решение опорным решением. Пусть получено опорное решение, например, для следующей задачи. Проверим, оптимально оно или нет.
, следовательно, эта вершина недопустима. Признаком недопустимости вершины является наличие отрицательных свободных членов в ограничениях равенствах. Если отрицательный свободный член есть, то надо перейти в другую вершину, для чего одну базисную переменную сделать свободной и приравнять к нулю, а какую-то свободную превратить в базисную. Следовательно, переход из одной вершины в другую осуществляется путем замены базисной переменной на свободную. Это называется симплекс-преобразованием. Если мы будем переходить из вершины в вершину «в сторону ОДР», то за конечное число таких переходов попадем в допустимую вершину. Назовем ее опорной вершиной, а соответствующее решение опорным решением. Пусть получено опорное решение, например, для следующей задачи. Проверим, оптимально оно или нет.
 ,
,
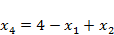 ,
,
 ,
,
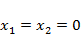 ;
;  ;
;  ;
; 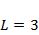 .
.
Видно, что если все коэффициенты при свободных переменных в целевой функции положительны, то никакие увеличения свободных переменных от 0 вверх не уменьшают  , следовательно, это
, следовательно, это  является оптимальным значением. Если же есть отрицательные коэффициенты при свободных переменных (в нашем примере при
является оптимальным значением. Если же есть отрицательные коэффициенты при свободных переменных (в нашем примере при  ), то ее надо сделать базисной, т.к. если она будет положительной, то
), то ее надо сделать базисной, т.к. если она будет положительной, то  будет меньше. Но
будет меньше. Но  может увеличиваться не бесконечно, так как в ограничениях есть отрицательный коэффициент при
может увеличиваться не бесконечно, так как в ограничениях есть отрицательный коэффициент при  . Видно, что увеличивать
. Видно, что увеличивать  можно только до
можно только до 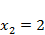 , так в противном случае
, так в противном случае  будет отрицательным, а это невозможно. Так мы нашли базисную переменную
будет отрицательным, а это невозможно. Так мы нашли базисную переменную  , которую надо поменять со свободной
, которую надо поменять со свободной  . Поиск этой пары для симплекс-преобразования и является основным элементом симплекс-метода.
. Поиск этой пары для симплекс-преобразования и является основным элементом симплекс-метода.
Таким образом, симплекс-метод – это метод решения задач ЛП, который основывается на процедуре перехода от одной вершины к другой до тех пор, пока не придем в оптимальную вершину. Он состоит из трех алгоритмов:
1. Алгоритм перехода из одной вершины в другую, когда известна пара пре образования. Он пересчитывает коэффициенты системы уравнений для нового базиса. Назовем его алгоритмом симплекс-преобразования.
2. Алгоритм нахождения такой пары преобразования, чтобы при переходе в новую вершину мы приближались к ОДР. Это алгоритм отыскания опорного решения.
3. Алгоритм нахождения такой пары преобразования, чтобы новая опорная вершина давала лучшее значение целевой функции. Это алгоритм отыскания оптимального решения.
 В симплекс-методе начинают со стандартной вершины (все свободные переменные равны нулю), т.е. с точки 1 (это недопустимая вершина, смотри рисунок справа). Дальше последовательно переходим из одной вершины в другую (2,3) и попадаем в опорную вершину 4.
В симплекс-методе начинают со стандартной вершины (все свободные переменные равны нулю), т.е. с точки 1 (это недопустимая вершина, смотри рисунок справа). Дальше последовательно переходим из одной вершины в другую (2,3) и попадаем в опорную вершину 4.
Найдя опорное решение, мы движемся по вершинам ОДР так, чтобы целевая функция улучшалась, и при этом эти вершины были опорными (5 и 6 – оптимальная). Эти три алгоритма гарантируют либо отыскание оптимального решения, либо доказательство отсутствия допустимого решения, либо доказательство отсутствия оптимального решения.
12.1Симплекс-таблица, стандартный алгоритм симплекс-преобразования
Существует много форм симплекс-таблиц (СТ). Мы рассмотрим наиболее компактную форму, в которой строки — базисные переменные, а столбцы свободные переменные. Каждая СТ содержит коэффициенты модели задачи ЛП. Для записи СТ необходимо представить ОЗЛП в стандартной форме:

т.е. на первом месте свободный член, а коэффициенты при свободных переменных меняют знак.


Рассмотрим порядок вычислений для перехода в новую вершину. Пусть нам необходимо выполнить симплекс-преобразование 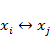 . Тогда нужно получить новую симплекс-таблицу. Для этого выполним алгоритм.
. Тогда нужно получить новую симплекс-таблицу. Для этого выполним алгоритм.
Алгоритм 1:
1. Отыскиваем в СТ элемент  и объявляем его генеральным. Тогда i-я строка и j -й столбец - генеральные.
и объявляем его генеральным. Тогда i-я строка и j -й столбец - генеральные.
2. Вычисляем величину, обратную генеральному элементу, и записываем ее в нижней части генеральной клетки:

3. Все элементы генеральной строки умножаем на 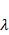 . Результат записываем в нижней части соответствующих клеток.
. Результат записываем в нижней части соответствующих клеток.
4. Все элементы генерального столбца умножаем на  . Результат записываем в нижней части клеток.
. Результат записываем в нижней части клеток.
5. Отмечаем верхние элементы генеральной строки и нижние элементы генерального столбца.
6. В каждой клетке, не принадлежащей ни генеральному столбцу, ни генеральной строке, в нижнюю часть записываем произведение отмеченных элементов, стоящих в том же столбце и той же строке, что и данная клетка.
7. Переписываем СТ, заменяя в соответствии с табл. 2:






 разрешены относительно свободных
разрешены относительно свободных  . Например,
. Например,



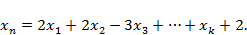
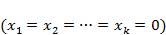 – вершина, при этом базисные переменные
– вершина, при этом базисные переменные  ,
,  ,
,  .
.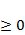 , следовательно, эта вершина недопустима. Признаком недопустимости вершины является наличие отрицательных свободных членов в ограничениях равенствах. Если отрицательный свободный член есть, то надо перейти в другую вершину, для чего одну базисную переменную сделать свободной и приравнять к нулю, а какую-то свободную превратить в базисную. Следовательно, переход из одной вершины в другую осуществляется путем замены базисной переменной на свободную. Это называется симплекс-преобразованием. Если мы будем переходить из вершины в вершину «в сторону ОДР», то за конечное число таких переходов попадем в допустимую вершину. Назовем ее опорной вершиной, а соответствующее решение опорным решением. Пусть получено опорное решение, например, для следующей задачи. Проверим, оптимально оно или нет.
, следовательно, эта вершина недопустима. Признаком недопустимости вершины является наличие отрицательных свободных членов в ограничениях равенствах. Если отрицательный свободный член есть, то надо перейти в другую вершину, для чего одну базисную переменную сделать свободной и приравнять к нулю, а какую-то свободную превратить в базисную. Следовательно, переход из одной вершины в другую осуществляется путем замены базисной переменной на свободную. Это называется симплекс-преобразованием. Если мы будем переходить из вершины в вершину «в сторону ОДР», то за конечное число таких переходов попадем в допустимую вершину. Назовем ее опорной вершиной, а соответствующее решение опорным решением. Пусть получено опорное решение, например, для следующей задачи. Проверим, оптимально оно или нет. ,
,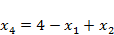 ,
, ,
,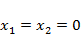 ;
;  ;
;  ;
; 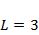 .
. , следовательно, это
, следовательно, это  ), то ее надо сделать базисной, т.к. если она будет положительной, то
), то ее надо сделать базисной, т.к. если она будет положительной, то 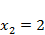 , так в противном случае
, так в противном случае  будет отрицательным, а это невозможно. Так мы нашли базисную переменную
будет отрицательным, а это невозможно. Так мы нашли базисную переменную  В симплекс-методе начинают со стандартной вершины (все свободные переменные равны нулю), т.е. с точки 1 (это недопустимая вершина, смотри рисунок справа). Дальше последовательно переходим из одной вершины в другую (2,3) и попадаем в опорную вершину 4.
В симплекс-методе начинают со стандартной вершины (все свободные переменные равны нулю), т.е. с точки 1 (это недопустимая вершина, смотри рисунок справа). Дальше последовательно переходим из одной вершины в другую (2,3) и попадаем в опорную вершину 4.


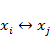 . Тогда нужно получить новую симплекс-таблицу. Для этого выполним алгоритм.
. Тогда нужно получить новую симплекс-таблицу. Для этого выполним алгоритм. и объявляем его генеральным. Тогда i-я строка и j -й столбец - генеральные.
и объявляем его генеральным. Тогда i-я строка и j -й столбец - генеральные.
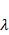 . Результат записываем в нижней части соответствующих клеток.
. Результат записываем в нижней части соответствующих клеток. . Результат записываем в нижней части клеток.
. Результат записываем в нижней части клеток.


