Определить истинную величину треугольника ABC(A’B’C’ , A’’B’’C’’) вращением вокруг горизонтали.
РЕШЕНИЕ:
Для решения задачи построим в треугольнике горизонталь h(h’, h’’), проходящую через одну из его вершин, например, вершину C(C’, C’’). В этом случае точкаCܥ не будет изменять своего положения при вращении, т.к. находится на оси вращения, т.е. C*≡C.
Вращение будет осуществляться до тех пор, пока плоскость треугольника не займет положение, параллельное горизонтальной плоскости проекций π1. При этом новая фронтальная проекция треугольника ABC совпадет с фронтальной проекцией горизонтали (на рисунке не показано). Построим новую горизонтальную проекцию треугольника, равную его истинной величине A*B*C*.
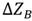
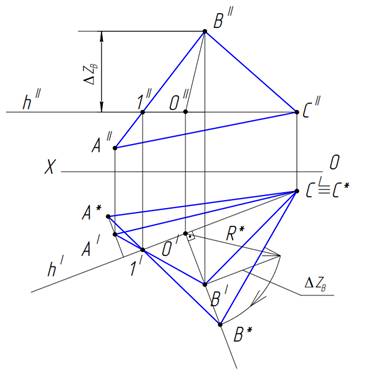
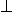 С этой целью проведем ФПГ C’’1’’// OX и в проекционной связи построим ГПГ C’1’. Центр вращения O(O’, O’’) точки B(B’,B”) найдем, опустив перпендикуляр из точки B’ на ГПГ (B’O’ C’1’). Этот перпендикуляр определяет горизонтальную проекцию траектории перемещения точки B при вращении. Истинную величину радиуса вращения R* найдем методом треугольника, откладывая на перпендикуляре к B’O’ алгебраическую разность - расстояние от точки B’’ до фронтальной проекции горизонтали h”.
С этой целью проведем ФПГ C’’1’’// OX и в проекционной связи построим ГПГ C’1’. Центр вращения O(O’, O’’) точки B(B’,B”) найдем, опустив перпендикуляр из точки B’ на ГПГ (B’O’ C’1’). Этот перпендикуляр определяет горизонтальную проекцию траектории перемещения точки B при вращении. Истинную величину радиуса вращения R* найдем методом треугольника, откладывая на перпендикуляре к B’O’ алгебраическую разность - расстояние от точки B’’ до фронтальной проекции горизонтали h”.
Полученный радиус R* перенесем на траекторию перемещения точки B’ , т.е. на продолжение отрезка B’O’. Полученная точка B* является новой горизонтальной проекцией вершины B треугольника.
Для нахождения нового положения вершины A≡A* можно либо выполнить построения аналогичные тем, что проводились для вершины B ,либо провести прямую из точки B* через неподвижную точку 1’ до пересечения с перпендикуляром, опущенным из точки A’ на ГПГ C’1’. С учетом неизменности положения вершины C*≡C, можно утверждать, что ∆A*B*C* есть истинная величина заданного треугольника.
21) Гранные поверхности. Примеры изображения на эпюре.
Гранные поверхности – поверхности, образованные перемещением прямолинейной образующей по ломаной линии (рис. 2.3).
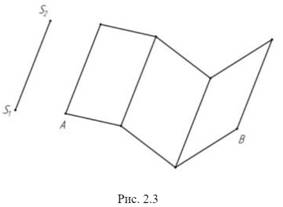
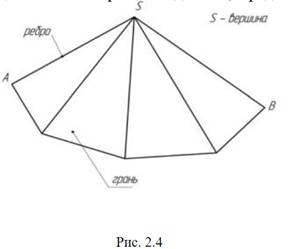 Многогранниками называются замкнутые пространственные фигуры, ограниченные плоскими многоугольниками (гранями). Линии пересечения граней называются ребрами, а точки пересечения ребер называются вершинами многогранника. Изображение на чертеже сводится к изображению ребер, т. е. линий пересечения граней, и вершин – точек пересечения ребер.
Многогранниками называются замкнутые пространственные фигуры, ограниченные плоскими многоугольниками (гранями). Линии пересечения граней называются ребрами, а точки пересечения ребер называются вершинами многогранника. Изображение на чертеже сводится к изображению ребер, т. е. линий пересечения граней, и вершин – точек пересечения ребер.
Пример изображения поверхности с направляющей АВ и образующей, одна точка которой неподвижна, представлен на рис. 2.4.
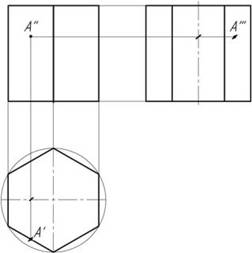 Призма – многогранник, две грани которого равные многоугольники, а остальные грани (принадлежащие боковой поверхности призмы) – четырехугольники (рис. 2.5).
Призма – многогранник, две грани которого равные многоугольники, а остальные грани (принадлежащие боковой поверхности призмы) – четырехугольники (рис. 2.5).
На поверхности боковой грани шестиугольной правильной призмы изображена точка А'' (видимая). Т. к. боковые грани находятся в горизонтально-проецирующих плоскостях, то на горизонтально плоскость проекций точки (А') проецируются на линию, в которую проецируется соответствующая грань. Профильная проекция точки А'''
построена по горизонтальной и фронтальной проекциям.
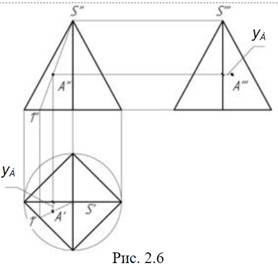 Пирамида – многогранник, одна грань которого многоугольник со сколь угодно большим числом сторон, а остальные грани – треугольники с общей вершиной (рис. 2.6). На боковой грани пирамиды изображена точка А '' (видимая). Поскольку грани пирамиды расположены наклонно ко всем плоскостям проекции (т. е. плоскостям общего положения), то для определения горизонтальной проекции точки А ' используют вспомогательную линию. Соединяя вершину (S '' ) с точкой А '' до основания получим точку 1 ''.
Пирамида – многогранник, одна грань которого многоугольник со сколь угодно большим числом сторон, а остальные грани – треугольники с общей вершиной (рис. 2.6). На боковой грани пирамиды изображена точка А '' (видимая). Поскольку грани пирамиды расположены наклонно ко всем плоскостям проекции (т. е. плоскостям общего положения), то для определения горизонтальной проекции точки А ' используют вспомогательную линию. Соединяя вершину (S '' ) с точкой А '' до основания получим точку 1 ''.
Поверхностью вращения называется поверхность, которая образуется произвольной кривой или прямой линией при ее вращении вокруг неподвижной оси.
Поверхности вращения получили самое широкое применение в технике, благодаря распространенности вращательного движения и простоте обработки поверхности вращения (рис. 2.7).
Каждая точка образующей вокруг оси вращения (O '', O1'' ) описывает окружность с центром на оси вращения. Эти окружности называются параллелями. Наибольшую параллель называют экватором, наименьшую – горлом.
Кривые, получающиеся в сечении тела вращения плоскостями, проходящими через ось вращения, называются меридианами. Меридиан, параллельный фронтальной плоскости проекции, называют главным меридианом (O '', A '', F '', B '', C '', D '', O1'' ).
На чертеже ось вращения поверхности располагают перпендикулярно к одной из плоскостей проекций (чаще горизонтальной), тогда все параллели проецируются на эту плоскость в истинную величину, причем экватор и горло определяют горизонтальный очерк поверхности.
Фронтальным очерком такой поверхности будет меридиан, расположенный во фронтальной плоскости проекции, т. е. главный меридиан.
Точки на поверхности тела вращения строят при помощи параллелей.
 Цилиндрическая поверхность образуется перемещением образующей (LM), сохраняющей во всех своих положениях параллельность некоторой заданной прямой (окружность) и проходящей последовательно через все точки кривой направляющей (рис. 2.8).
Цилиндрическая поверхность образуется перемещением образующей (LM), сохраняющей во всех своих положениях параллельность некоторой заданной прямой (окружность) и проходящей последовательно через все точки кривой направляющей (рис. 2.8).
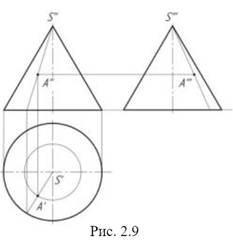 Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки кривой направляющей (окружности) (рис. 2.9).
Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки кривой направляющей (окружности) (рис. 2.9).
Даны комплексный чертеж конуса и фронтальная проекция точки A '' (видимая), принадлежащей боковой поверхности конуса. В качестве вспомогательной линии используем образующую SA. Сначала проводим ее фронтальную проекцию, затем горизонтальную и профильную. Проекции точки А лежат на одноименных проекциях образующих.
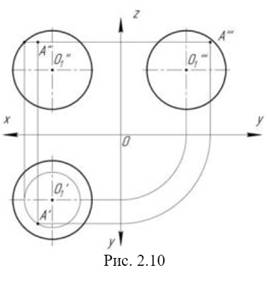
Сфера – это поверхность, которая получается в результате вращения окружности вокруг своей оси (рис. 2.10).
22) Поверхность вращения. Определение, примеры.
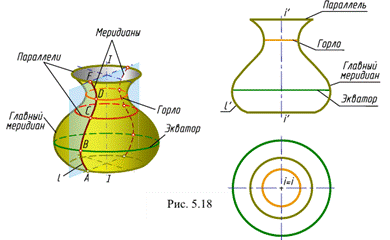 Поверхностью вращения называется поверхность, описываемая кривой (или прямой) образующей при ее вращении вокруг неподвижной оси (рис. 5.18). Эта поверхность определяется на чертеже заданием образующей и оси вращения.
Поверхностью вращения называется поверхность, описываемая кривой (или прямой) образующей при ее вращении вокруг неподвижной оси (рис. 5.18). Эта поверхность определяется на чертеже заданием образующей и оси вращения.
На чертеже ось вращения 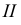 располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.
располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.
Точки на поверхностях вращения могут быть построены с помощью параллелей, то есть окружностей на поверхности (рис. 5.20, рис. 5.22, а, б, в, рис. 5.23 - рис. 5.25).
Рассмотрим некоторые тела и поверхности вращения.
1 .Поверхности, образованные вращением прямой линии:
а) цилиндр вращения - поверхность, полученная вращением прямой 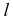 вокруг параллельной ей оси
вокруг параллельной ей оси 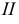 (рис. 5.19);
(рис. 5.19);
б) конус вращения - поверхность, образованная вращением прямой 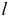 вокруг пересекающейся с ней осью
вокруг пересекающейся с ней осью 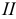 (рис. 5.20);
(рис. 5.20);
в) однополостный гиперболоид вращения - поверхность, полученная вращением прямой 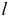 вокруг скрещивающейся с ней осью
вокруг скрещивающейся с ней осью  (рис. 5.21).
(рис. 5.21).
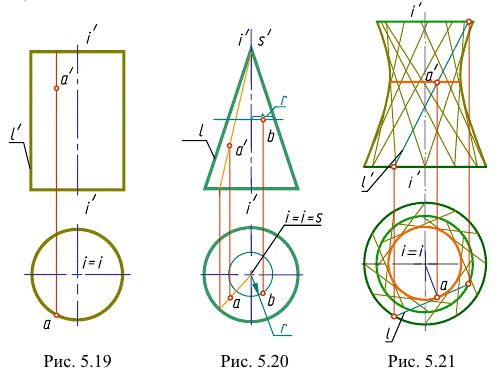
Точка А, лежащая на перпендикуляре к оси вращения и образующей, будет описывать наименьшую окружность, являющуюся горлом гиперболоида. Однополостный гиперболоид может быть также получен вращением гиперболы вокруг ее мнимой оси.
2. Поверхности, образованные вращением окружности вокруг неподвижной оси: а) сфера - поверхность, полученная вращением окружности вокруг ее диаметра (рис. 5. 22, а);
б) тор - поверхность, полученная вращением окружности вокруг оси 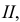 лежащей в плоскости этой окружности, но не проходящей через ее центр (рис. 5.22, б-д).
лежащей в плоскости этой окружности, но не проходящей через ее центр (рис. 5.22, б-д).
 Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор - кольцо» (рис. 5.22, б); если ось касается окружности, то образованная поверхность называются «закрытый тор» (рис. 5.22, в); если ось пересекает окружность - «самопересекающийся тор» (рис. 5.22, г, д)). Тор, изображенный на рис. 5.22, г, называется также «тор-яблоко», а на рис. 5.22, д — «тор-лимон». Сфера - частный случай торовой поверхности.
Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор - кольцо» (рис. 5.22, б); если ось касается окружности, то образованная поверхность называются «закрытый тор» (рис. 5.22, в); если ось пересекает окружность - «самопересекающийся тор» (рис. 5.22, г, д)). Тор, изображенный на рис. 5.22, г, называется также «тор-яблоко», а на рис. 5.22, д — «тор-лимон». Сфера - частный случай торовой поверхности.
3. Поверхности вращения, образованные вращением кривых второго порядка:
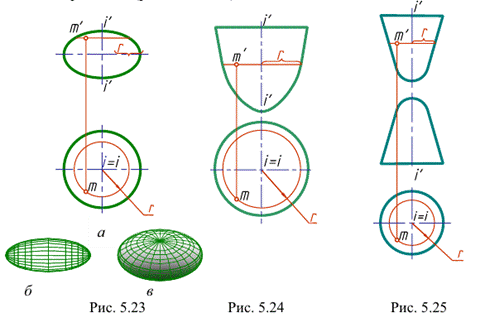 а) эллипсоид вращения - поверхность, полученная вращением эллипса вокруг оси (рис. 5.23). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вращения (рис. 5.23, б), при вращении вокруг малой оси - сжатым элипсоидом вращения (рис. 5.23, а, в);
а) эллипсоид вращения - поверхность, полученная вращением эллипса вокруг оси (рис. 5.23). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вращения (рис. 5.23, б), при вращении вокруг малой оси - сжатым элипсоидом вращения (рис. 5.23, а, в);
б) параболоид вращения - поверхность, образованная вращением параболы вокруг ее оси (рис. 5.24);
в) двухполостный гиперболоид вращения - поверхность, образованная вращением гиперболы вокруг ее действительной оси (рис. 5.25).



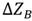
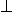 С этой целью проведем ФПГ C’’1’’// OX и в проекционной связи построим ГПГ C’1’. Центр вращения O(O’, O’’) точки B(B’,B”) найдем, опустив перпендикуляр из точки B’ на ГПГ (B’O’ C’1’). Этот перпендикуляр определяет горизонтальную проекцию траектории перемещения точки B при вращении. Истинную величину радиуса вращения R* найдем методом треугольника, откладывая на перпендикуляре к B’O’ алгебраическую разность - расстояние от точки B’’ до фронтальной проекции горизонтали h”.
С этой целью проведем ФПГ C’’1’’// OX и в проекционной связи построим ГПГ C’1’. Центр вращения O(O’, O’’) точки B(B’,B”) найдем, опустив перпендикуляр из точки B’ на ГПГ (B’O’ C’1’). Этот перпендикуляр определяет горизонтальную проекцию траектории перемещения точки B при вращении. Истинную величину радиуса вращения R* найдем методом треугольника, откладывая на перпендикуляре к B’O’ алгебраическую разность - расстояние от точки B’’ до фронтальной проекции горизонтали h”.

 Многогранниками называются замкнутые пространственные фигуры, ограниченные плоскими многоугольниками (гранями). Линии пересечения граней называются ребрами, а точки пересечения ребер называются вершинами многогранника. Изображение на чертеже сводится к изображению ребер, т. е. линий пересечения граней, и вершин – точек пересечения ребер.
Многогранниками называются замкнутые пространственные фигуры, ограниченные плоскими многоугольниками (гранями). Линии пересечения граней называются ребрами, а точки пересечения ребер называются вершинами многогранника. Изображение на чертеже сводится к изображению ребер, т. е. линий пересечения граней, и вершин – точек пересечения ребер. Призма – многогранник, две грани которого равные многоугольники, а остальные грани (принадлежащие боковой поверхности призмы) – четырехугольники (рис. 2.5).
Призма – многогранник, две грани которого равные многоугольники, а остальные грани (принадлежащие боковой поверхности призмы) – четырехугольники (рис. 2.5). Пирамида – многогранник, одна грань которого многоугольник со сколь угодно большим числом сторон, а остальные грани – треугольники с общей вершиной (рис. 2.6). На боковой грани пирамиды изображена точка А '' (видимая). Поскольку грани пирамиды расположены наклонно ко всем плоскостям проекции (т. е. плоскостям общего положения), то для определения горизонтальной проекции точки А ' используют вспомогательную линию. Соединяя вершину (S '' ) с точкой А '' до основания получим точку 1 ''.
Пирамида – многогранник, одна грань которого многоугольник со сколь угодно большим числом сторон, а остальные грани – треугольники с общей вершиной (рис. 2.6). На боковой грани пирамиды изображена точка А '' (видимая). Поскольку грани пирамиды расположены наклонно ко всем плоскостям проекции (т. е. плоскостям общего положения), то для определения горизонтальной проекции точки А ' используют вспомогательную линию. Соединяя вершину (S '' ) с точкой А '' до основания получим точку 1 ''. Цилиндрическая поверхность образуется перемещением образующей (LM), сохраняющей во всех своих положениях параллельность некоторой заданной прямой (окружность) и проходящей последовательно через все точки кривой направляющей (рис. 2.8).
Цилиндрическая поверхность образуется перемещением образующей (LM), сохраняющей во всех своих положениях параллельность некоторой заданной прямой (окружность) и проходящей последовательно через все точки кривой направляющей (рис. 2.8). Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки кривой направляющей (окружности) (рис. 2.9).
Коническая поверхность образуется прямой линией, проходящей через некоторую неподвижную точку и последовательно через все точки кривой направляющей (окружности) (рис. 2.9).
 Поверхностью вращения называется поверхность, описываемая кривой (или прямой) образующей при ее вращении вокруг неподвижной оси (рис. 5.18). Эта поверхность определяется на чертеже заданием образующей и оси вращения.
Поверхностью вращения называется поверхность, описываемая кривой (или прямой) образующей при ее вращении вокруг неподвижной оси (рис. 5.18). Эта поверхность определяется на чертеже заданием образующей и оси вращения.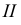 располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.
располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.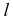 вокруг параллельной ей оси
вокруг параллельной ей оси 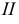 (рис. 5.19);
(рис. 5.19);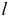 вокруг пересекающейся с ней осью
вокруг пересекающейся с ней осью 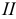 (рис. 5.20);
(рис. 5.20);
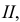 лежащей в плоскости этой окружности, но не проходящей через ее центр (рис. 5.22, б-д).
лежащей в плоскости этой окружности, но не проходящей через ее центр (рис. 5.22, б-д). Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор - кольцо» (рис. 5.22, б); если ось касается окружности, то образованная поверхность называются «закрытый тор» (рис. 5.22, в); если ось пересекает окружность - «самопересекающийся тор» (рис. 5.22, г, д)). Тор, изображенный на рис. 5.22, г, называется также «тор-яблоко», а на рис. 5.22, д — «тор-лимон». Сфера - частный случай торовой поверхности.
Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор - кольцо» (рис. 5.22, б); если ось касается окружности, то образованная поверхность называются «закрытый тор» (рис. 5.22, в); если ось пересекает окружность - «самопересекающийся тор» (рис. 5.22, г, д)). Тор, изображенный на рис. 5.22, г, называется также «тор-яблоко», а на рис. 5.22, д — «тор-лимон». Сфера - частный случай торовой поверхности. а) эллипсоид вращения - поверхность, полученная вращением эллипса вокруг оси (рис. 5.23). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вращения (рис. 5.23, б), при вращении вокруг малой оси - сжатым элипсоидом вращения (рис. 5.23, а, в);
а) эллипсоид вращения - поверхность, полученная вращением эллипса вокруг оси (рис. 5.23). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вращения (рис. 5.23, б), при вращении вокруг малой оси - сжатым элипсоидом вращения (рис. 5.23, а, в);

