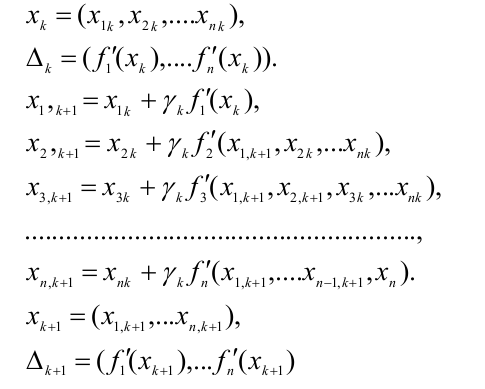Вариант 1
Выполнил: Студентгруппы ИВТ-41-15
Агниашвили Д.В.
Проверила:Первова Н.В.
Чебоксары2017.

Задание на работу
1. Построить график функции y=f(x) на отрезке [x0, x1].
2. Найти корень заданного уравнения f(x)=0 с заданной точностью ε на заданном отрезке [x0, x1].
3. Привести расчёты параметров итерационного процесса для каждого шага алгоритма.
4. Решить исходное уравнение с помощью встроенной функции roots, fzero, sqp.
5. Сравнить результаты, полученные в п.2 и 4.
6. Записать в ответе только верные цифры


Алгоритм
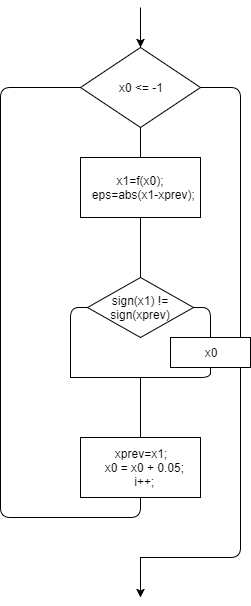
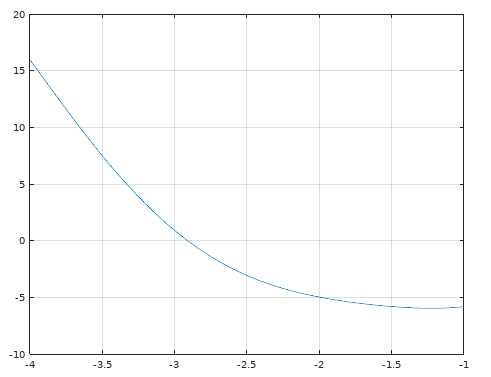
График заданной функции
Значения параметров итерационного процесса для каждого
Шага алгоритма в виде сводной таблицы
| N
| X0
| X1
| c
| F(x0)
| F(x1)
| F(c) <eps
|
| 1
| -2.8425
| -2.8425
| 0.15748
| 0.92789
| -0.031976
| 0
|
| 2
| -2.9045
| -2.9045
| -0.061952
| -0.60174
| 0.0012211
| 1
|
Решения исходного уравнения с помощью встроенных функций roots, fzero, sqp.
X= -2.9078
Анализ результатов решения уравнения и выводы по работе.
Точка x0 = -2.9000
Точка x0fzero = -2.9078
Значение x при помощи встроенных функций sqp = -2.9078
i = 61
Текст программы
x=-4:0.05:-1;
function y=f(x) y=(sin(x).*x.*x+5.*cos(5.*exp(x/2)));
end;
plot(x,f(x));
grid on;
f=inline('(sin(x).*x.*x+5.*cos(5.*exp(x/2)))');
x0=-3;
x1=-2;
eps=0.05;
tmp=0;
n=1;
x1=x1-(x1-x0)*f(x1)/(f(x1)-f(x0));
while (abs(x1-x0)>eps)
c = x1-x0
tmp=x1
f(x0)
f(x1)
x1=x1-(x1-x0)*f(x1)/(f(x1)-f(x0));
x0=tmp
printf("====\n")
n++;
endwhile
x1
n
fzero(f,[-3;-2])
x0=-3;
x1=-2;
n=1;
x1=x1-(x1-x0)*f(x1)/(f(x1)-f(x0));
while (abs(x1-x0)>eps)
tmp=x1;
x1=x1-(x1-x0)*f(x1)/(f(x1)-f(x0));
x0=tmp;
n++;
endwhile
x1
n
%hold on;
fzero(f,[-3;-2])
f1=inline('abs(sin(x).*x.*x+5.*cos(5.*exp(x/2)))');
[x,obj,info,iter]=sqp(-3,f1)
[x,obj,info,iter]=sqp(-2,f1)
Выводы по работе.
Изучил основы программирования на Octave, применил полученные навыки в написании программ по решению нелинейных трансцендентных уравнений.
ФГБОУ ВО «Чувашский государственный университет им.И.Н.Ульянова»
Факультет информатики и вычислительной техники
Кафедра вычислительной техники
Вычислительная математика
Лабораторная работа №2
«Решение нелинейных трансцендентных уравнений»
Вариант 1
Выполнил: Студент группы ИВТ-41-15
Агниашвили Д.В.
Проверила:Первова Н.В.
Чебоксары 2017.

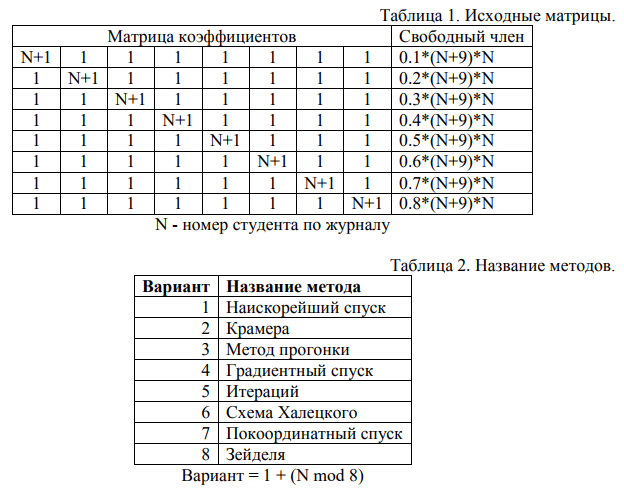
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
1. В итерационных методах предусмотреть выход в случае зацикливания программы.


Исходная матрица:
| Матрица коэффициентов
| Свободный член
|
| 20
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 53.2
|
| 1
| 20
| 1
| 1
| 1
| 1
| 1
| 1
| 106.4
|
| 1
| 1
| 20
| 1
| 1
| 1
| 1
| 1
| 159.6
|
| 1
| 1
| 1
| 20
| 1
| 1
| 1
| 1
| 212.8
|
| 1
| 1
| 1
| 1
| 20
| 1
| 1
| 1
| 266
|
| 1
| 1
| 1
| 1
| 1
| 20
| 1
| 1
| 319.2
|
| 1
| 1
| 1
| 1
| 1
| 1
| 20
| 1
| 372.4
|
| 1
| 1
| 1
| 1
| 1
| 1
| 1
| 20
| 425.6
|
Общий Алгоритм:
Я решил использовать метод наискорейшего спуска. 1. Задать (произвольно) точку начального приближения x(0);2. В цикле по номеру итерации k=0,1,… вычислить:3. Значение вектора градиента в точке x=x(k) по формуле
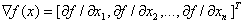
4. Значение нормы (длины) вектора градиента по
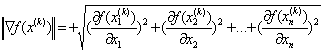
5. Значение вектора единичной длины в направлении, противоположном вектору градиента s(k) по формуле
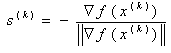
6. Значение матрицы вторых производных по
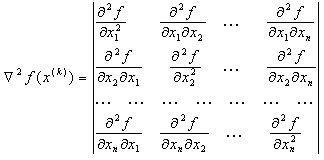
7. Значение шага по
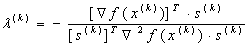
8. Новое значение приближения x(k+1) по

9. Закончить итерационный процесс, используя условие: следует прекратить вычисления, если, начиная с k* - той итерации абсолютное значение нормированной разности между значениями функции в “соседних” не превышает наперед заданного малого числа
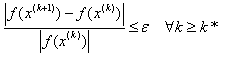
Алгоритм для решения СЛАУ: (на псевдокоде)
A,B - входная матрица и матрица свободных членов
x0 = 0
x1 = 0
r = 0
r1 = 0
k = 0;
kMax = 100; - максимальное число итераций, на случай зацикливания
eps = 0.0001; - точность
repeat
for i = 1 to 8 do
r(i) <- B(i);
for j = 1 to 8 do
r(i) -= A(i,j)*x0(j);
s = 0;
s1 = 0;
for i = 1 to 8 do
s += r(i)^2;
r1(i) = 0;
for j = 1 to 8 do
r1(i) += A(i,j)*r(j);
s1 += r(i)*r1(i);
s = s / s1;
for i=1 to 8 do
x1(i) += s*r(i);
s=0;
for i=1:8
s += (x0(i) - x1(i))*(x0(i) - x1(i));
x0(i) = x1(i);
k++;
until (k >= kMax) ИЛИ (sqrt(s) <= eps)
Вывод(x1)
Результат работы алгоритма:

Невязка:

Максимальная невязка = X*A-B = -6.795*10-5 = -0,00006795
Метод вычисления: Метод Гаусса
Алгоритм решения:
Создаётся единичная матрица размером NxN. При помощи простейших преобразований из матрицы А получаем единичную матрицу, параллельно проводя те же действия с данной единичной матрицей. В итоге на месте единичной матрицы будет находится обратная к А.
Обратная матрица
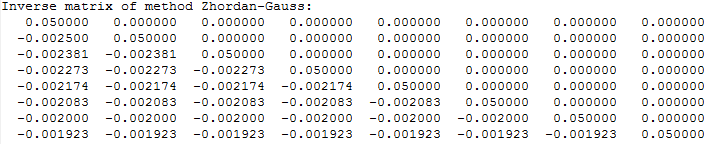
Решение:

Метод вычисления: с помощью стандартных функций inv(A), mldivide и fsolve.
Cпомощью inv(A):

Cпомощью mldivide:
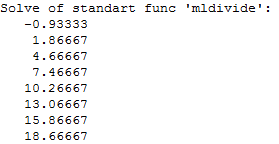
Cпомощью fsolve:
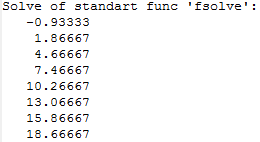
Листинг программы:
A = [ 2, 1, 1, 1, 1, 1, 1, 1;
1, 2, 1, 1, 1, 1, 1, 1;
1, 1, 2, 1, 1, 1, 1, 1;
1, 1, 1, 2, 1, 1, 1, 1;
1, 1, 1, 1, 2, 1, 1, 1;
1, 1, 1, 1, 1, 2, 1, 1;
1, 1, 1, 1, 1, 1, 2, 1;
1, 1, 1, 1, 1, 1, 1, 2;
]
B = [ 1;2;3;4;5;6;7;8; ]
Вычисление методом Градиентного спуска:
x0 = [ 0; 0; 0; 0; 0; 0; 0; 0 ];
x1 = [ 0; 0; 0; 0; 0; 0; 0; 0 ];
r = [ 0; 0; 0; 0; 0; 0; 0; 0 ];
r1 = [ 0; 0; 0; 0; 0; 0; 0; 0 ];
k = 0;
kMax = 100;
eps = 0.0001;
do
for i=1:8
r(i)=B(i);
for j=1:8
r(i) -= A(i,j)*x0(j);
end;
end;
s = 0;
s1 = 0;
for i=1:8
s += r(i)^2;
r1(i) = 0;
for j=1:8
r1(i) += A(i,j)*r(j);
end;
s1 += r(i)*r1(i);
end;
s = s / s1;
for i=1:8
x1(i) += s*r(i);
end;
s=0;
for i=1:8
s += (x0(i) - x1(i))*(x0(i) - x1(i));
x0(i) = x1(i);
end;
k++;
until (k >= kMax) || (sqrt(s) <= eps)
printf("Gradient solve:\n k = %i\n", k);
disp(x1);
printf("Discrepancy:\n");
disp(A*x1-B);
Вычисление методом Гаусса:
printf("\n\n");
Ae = [ A B ];
E = eye(8);
for j=1:7
for i=1+j:8
s=Ae(i,j)/Ae(j,j);
Ae(i,:)=Ae(i,:)-s*Ae(j,:);
E(i,:)=E(i,:)-s*E(j,:);
end;
end;
for j=0:7
for i=1:(7-i)
s=Ae(7-i,8-j)/Ae(8-j,8-j);
Ae(7-i,:)=Ae(i,:)-s*Ae(8-j,:);
E(7-i,:)=E(i,:)-s*E(8-j,:);
end;
end;
Ae = Ae(:,9)/Ae(8,8);
printf("Inverse matrix of method Zhordan-Gauss:\n");
invA = E/A(8,8);
disp(invA);
printf("\nSolve of method Zhordan-Gauss:\n");
disp(Ae);
Вычисление встроенными функциями:
printf("\n\nSolve of standart inverse matrix:\n");
X=A^(-1)*B;
disp(X);
printf("Solve of standartfunc 'mldivide':\n");
mld = mldivide(A,B);
disp(mld);
printf("Solve of standartfunc 'fsolve':\n");
xFslv = 0;
function [y] = myfunc(x)
y = zeros(8,1);
y(1) = 2*x(1)+x(2)+x(3)+x(4)+x(5)+x(6)+x(7)+x(8)-1;
y(2) = x(1)+2*x(2)+x(3)+x(4)+x(5)+x(6)+x(7)+x(8)-2;
y(3) = x(1)+x(2)+2*x(3)+x(4)+x(5)+x(6)+x(7)+x(8)-3;
y(4) = x(1)+x(2)+x(3)+2*x(4)+x(5)+x(6)+x(7)+x(8)-4;
y(5) = x(1)+x(2)+x(3)+x(4)+2*x(5)+x(6)+x(7)+x(8)-5;
y(6) = x(1)+x(2)+x(3)+x(4)+x(5)+2*x(6)+x(7)+x(8)-6;
y(7) = x(1)+x(2)+x(3)+x(4)+x(5)+x(6)+2*x(7)+x(8)-7;
y(8) = x(1)+x(2)+x(3)+x(4)+x(5)+x(6)+x(7)+2*x(8)-8;
end;
[xFslv, fval, info]=fsolve(@myfunc, [0;0;0;0;0;0;0;0]);
disp(xFslv);
Выводы по работе.
Изучил основы программирования на Octave, применил полученные навыки в написании программ порешению нелинейных трансцендентных уравнений.
ФГБОУ ВО «Чувашский государственный университет им.И.Н.Ульянова»
Факультет информатики и вычислительной техники
Кафедра вычислительной техники
Вычислительная математика
Лабораторная работа №3
«Решение систем нелинейных уравнений»
Вариант 1
Выполнил: Студент группы ИВТ-41-15
Агниашвили Д.В.
Проверила:Первова Н.В.
Чебоксары 2017.





x1 = linspace(-5,5);
y2 = linspace(-5,5);
y1=(2-sin(x1))/2;
x2=0.7-cos(y2-1);
%plot(x1,y1, x2,y2);
x = y = -2:0.01:2;
[xx, yy] = meshgrid(x, y);
z = (sin(xx)+2*yy-2)^2+(cos(yy-1)+xx-0.7)^2;
%mesh(x, y, z);
ezmeshc("(sin(x)+2*y-2)^2+(cos(y-1)+x-0.7)^2", [-10, 10, -5, 5]);
%ezcontour("(sin(x)+2*y-2)^2+(cos(y-1)+x-0.7)^2", [-10, 10, -5, 5]);
%================================================
function [res] = f(x)
res(1,1) = cos(x(1));
res(1,2) = 2;
res(2,1) = 1;
res(2,2) = -sin(x(2)-1);
end;
function [res] = fd(x)
res(1,1) = sin(x(1))+2*x(2)-2;
res(2,1) = x(1)+cos(x(2)-1)-0.7;
end;
e = 0.001;
k = 0;
x = [1;1];
t = [0;1];
while abs(max(x-t)) > e
t = x;
x = t-(inv(f(x))*fd(x));
k++;
end;
printf("x = %f\ny = %f\nK = %i\n\n", x(1), x(2), k);
%================================================
x1=0; x2=0;
y1=0; y2=1;
h=0.5;
e=0.001;
k = 0;
f=@(x1,x2) ((2-sin(x1))/2) - (asin(0.7-x2)+1);
while (abs(y2-y1) > e)
x1 += h;
y1 = f(x1,x2);
x2 += h;
y2 = f(x1,x2);
if (y2-y1 > 0)
h = -h/3;
end;
k++;
end;
printf("x0 = %f\ny0 = %f\nK = %i\n", x1, ((2-sin(x1))/2), k);
%================================================
e = 0.001;
x0 = [0;0];
function result = F(x)
result = (sin(x(1))+2*x(2)-2)^2+(cos(x(2)-1)+x(1)-0.7)^2;
end;
[x,obj,info,iter] = sqp(x0,@F,@F,@F,-10,10,1000,e^2)
Задание и исходные данные к лабораторной работе.
1. Отделить графически корни системы нелинейных уравнений (таблица 3).
2. Уточнить приближенное решение из п.1 методом Ньютона-Рафсона с точностями
e =1E-2,1E-3,1E-5 из трех различных начальных точек.
3. Уточнить приближенное решение из п.1 одним из указанных в таблице 4 методом
уточнения корней с точностью e =1E-2,1E-3,1E-5.
4. Сравнить результаты, полученные в п.2-3 задания, по количеству итераций
уточнения корней системы уравнений.
5. Найти решения системы нелинейных уравнений, а также информацию о процессе
нахождении минимума функции (функционала) с помощью стандартной функции
OCTAVE sqp с точностью e=1E-2, 1E-3, 1E-5.
Метод для уточнения корней - градиентный спуск.
Система уравнений, предлагаемая для решения:
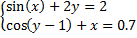 (1)
(1)
Текст программы
disp("Start\n");
function y=F(x)
y = (sin(x(1))+2*x(2)-2).^2+(cos(x(2)-1)+x(1)-0.7).^2;
endfunction
y=x=[-5:0.1:5];
[xx,yy] = meshgrid(x,y);
z = (sin(xx)+2*yy-2).^2+(cos(yy-1)+xx-0.7).^2;
mesh(x,y,z);
disp("Using SQP function");
X = [0,0];
[x, obj, info, iter] = sqp (X, @F)
disp("Gradient descent");
grad_x = inline('2*(cos(x)*sin(x)+2*y-2)+x+cos(1-y)-0.7');
grad_y = inline('4*(sin(x)+2*y-2)+2*sin(1-y)*(x+cos(1-y)-0.7)');
X = [0;0];
EPS = 1e-5;
n = 0;
grad = [];
h = 0.182;
do
tmp = X;
grad(1,:) = grad_x(X(1),X(2));
grad(2,:) = grad_y(X(1),X(2));
X = X - h*grad;
n++;
until (abs(F(X)-F(tmp))<=EPS);
X
n
disp("Newton-Raphson's method");
w1 = inline('sin(x)+2*y-2');
w2 = inline('cos(y-1)+x-0.7');
J1 = inline('cos(x)');
J2 = 2;
J3 = 1;
J4 = inline('sin(1-y)');
n = 0;
X = [0;0];
do
w = [ w1(X(1),X(2)); w2(X(1),X(2))];
Jacobian = [ J1(X(1)), J2; J3, J4(X(2)) ];
delta = inv(Jacobian)*w;
X = X - delta;
n++;
until (abs(delta) <= EPS)
X
n
Задание и исходные данные к лабораторной работе.
F1(x,y) = cos(x-1)+y=0.5
F2(x,y) = x-cos(y)=3
Метод наискорейшего спуска
Алгоритм
На каждом шаге метод «приближается» к решению последовательно покаждой из координат. Переход от точки х к к точке х к+1 назовем внешнейитерацией. Внутри каждой «внешней» итерации находятся n внутреннихдля последовательного вычисления координат точки х к+1
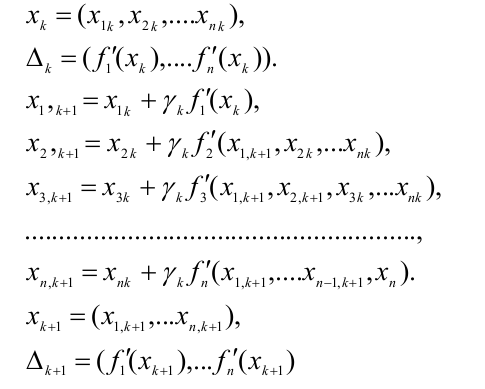
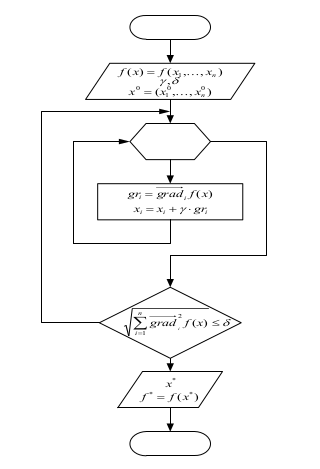
1. Поверхностьфункционаласистемы:
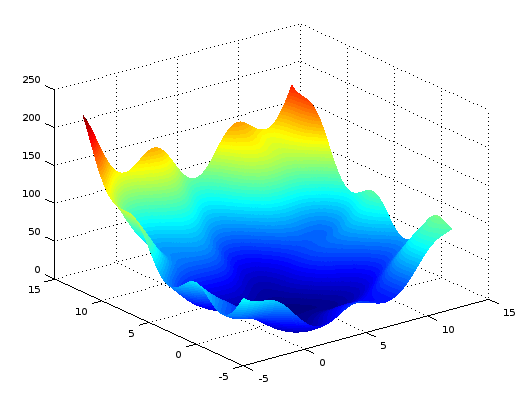
2. ОпределимВизуальноминимумфункционала:
x = 4;
y = 1.5;
3. Графикилинийуровняфункционала:
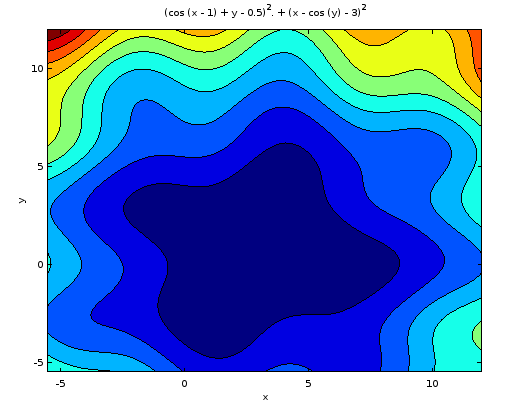
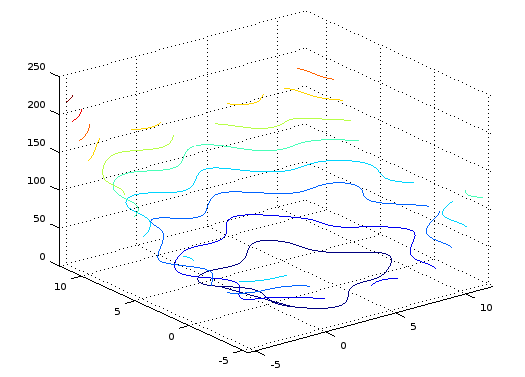
4. Результатырешенияразнымиметодами:
Уточнение корней:
| eps
| Метод Ньютона -Рафсона
| Наискорейший спуск
| Функция spq
|
| 1E-2
|
x1 = 3.3559
y1 = 1.2069
| ans = 4
3.3562 1.2070
| x =
3.3559
1.2069
obj = 1.4379e-16
info = 101
iter = 7
|
| 1E-3
| x1 = 3.3559
y1 = 1.2069
| ans = 5
3.3559 1.2069
| x =
3.3559
1.2069
obj = 1.7616e-16
info = 101
iter = 9
|
| 1E-5
| x1 = 3.3559
y1 = 1.2069
| ans = 8
3.3559 1.2069
| x =
3.3559
1.2069
obj = 1.7423e-16
info = 101
iter = 13
|
x(0) = [4; 1.5](Наискорейший спуск и метод Ньютона-Рафсона)
начальный шаг равен 0.3.(Наискорейший спуск)
Тексты программ
%главнаяпрограмма
y=x=[-5.5:0.01:12];
[xx, yy] = meshgrid (x, y);
z=(cos(xx-1)+yy-0.5).^2.+(xx-cos(yy)-3).^2;
%mesh(x,y,z)
%x0 = [4,1.5];
%[x,obj,info,iter] = sqp(x0,@phi)
fq = @(x,y) (cos(x-1)+y-0.5).^2.+(x-cos(y)-3).^2;
%ezcontourf (fq, [-5.5, 12],200);
%contour3(x,y,z)
%функционал
function y = phi(x)
y = (cos(x(1)-1)+x(2)-0.5).^2+(x(1)-cos(x(2))-3).^2;
endfunction;
%методЗейделя-Гаусса
functionXm = GaussSeidelMin(phi, x0, d, g)
% минимизацияпокоординатнымспуском (методГаусса-Зейделя)
% Xm - координтаыминимума
% phi - функциядвухпеременных, котойищетсяминиммум
% x0 - координатыначальнойточки
% d - точность
% g - постояннаяшага
k = 1; %Счетчикшагов
kmax =500; % Предельноечислошагов,
% задаетсядляпредотвращениязацикливания
% Массивыдляхраненияпромежуточныхкоординат
x1 = x0(1);
x2 = x0(2);
x1trace = [x1];
x2trace = [x2];
i = 2;
h = 1e-5; % приращениедлярассчетаградиентов
whilek<kmax
% Спускпопервойкоординате
gr1 = (phi(x1+h,x2)-phi(x1-h,x2))/(2*h); % производнаяпох1
x1 = x1 - g*gr1;
% Сохранениекоординат
x1trace(i) = x1;
x2trace(i) = x2;
i = i + 1;
% Спускповторойкоординате
gr2 = (phi(x1,x2+h)-phi(x1,x2-h))/(2*h); % производнаяпох2
x2 = x2 - g*gr2;
% Сохранениекоординат
x1trace(i) = x1;
x2trace(i) = x2;
i = i + 1;
% Проверкаусловияостанова
ifsqrt(gr1^2 + gr2^2) <= d;
break; % Выходизциклавслучаевыполненияусловия
end
k = k + 1;
end
Xm = [x1, x2]; % координатыминимума
ifk>= kmax
disp('Минимумненайден!')
disp('Изменитезначениешага')
end
k
endfunction;
function newton = Func(x)
newton = [0; 0];
newton(1) = cos(x(1)-1)+x(2)-0.5;
newton(2) = x(1)-cos(x(2))-3;
endfunction;
GaussSeidelMin(fq, [4,1.5], 1e-2, 0.3);
cur_x = [10; 10];
Eps = 1e-5;
delta = 0;
count = 0;
do
count++;
W = [-sin(-1+cur_x(1)), 4; 1.5, sin(cur_x(2))];
B = (-1)*Func(cur_x);
delta = inv(W)*B;
cur_x += delta;
until (max(abs(delta)) <Eps || count > 1000);
disp('МетодНьютона-Рафсона')
x
y
count
Вариант 1
Выполнил: Студентгруппы ИВТ-41-15
Агниашвили Д.В.
Проверила:Первова Н.В.
Чебоксары2017.

Задание на работу
1. Построить график функции y=f(x) на отрезке [x0, x1].
2. Найти корень заданного уравнения f(x)=0 с заданной точностью ε на заданном отрезке [x0, x1].
3. Привести расчёты параметров итерационного процесса для каждого шага алгоритма.
4. Решить исходное уравнение с помощью встроенной функции roots, fzero, sqp.
5. Сравнить результаты, полученные в п.2 и 4.
6. Записать в ответе только верные цифры


Алгоритм

График заданной функции

Значения параметров итерационного процесса для каждого











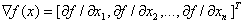 4. Значение нормы (длины) вектора градиента по
4. Значение нормы (длины) вектора градиента по 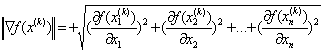 5. Значение вектора единичной длины в направлении, противоположном вектору градиента s(k) по формуле
5. Значение вектора единичной длины в направлении, противоположном вектору градиента s(k) по формуле 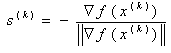 6. Значение матрицы вторых производных по
6. Значение матрицы вторых производных по 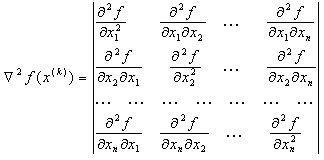 7. Значение шага по
7. Значение шага по 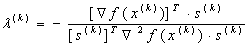 8. Новое значение приближения x(k+1) по
8. Новое значение приближения x(k+1) по  9. Закончить итерационный процесс, используя условие: следует прекратить вычисления, если, начиная с k* - той итерации абсолютное значение нормированной разности между значениями функции в “соседних” не превышает наперед заданного малого числа
9. Закончить итерационный процесс, используя условие: следует прекратить вычисления, если, начиная с k* - той итерации абсолютное значение нормированной разности между значениями функции в “соседних” не превышает наперед заданного малого числа 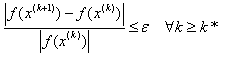












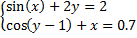 (1)
(1)