Число всех подмн-в n -элементного множества
|B(S)| = 2ⁿ
Док-во
Даны А и В, причем число элементов А задано и сущ-т биекция φ: A->B, тогда |B| = |A|
АсS, A->  = (x₁ x₂ … xn), xi= 1, если принадлежит и 0, если иначе. Φ – мн-во всех бинарных посл-тей длины 2. Т.к. отображение φ – биективно{0;1} =>
= (x₁ x₂ … xn), xi= 1, если принадлежит и 0, если иначе. Φ – мн-во всех бинарных посл-тей длины 2. Т.к. отображение φ – биективно{0;1} =>  = 2ⁿ.
= 2ⁿ.
3 Число r -сочетаний из n элементов. Биномиальнаятеорема и следствия из нее. Основны e свойства биномиальных коэффициентов. Треугольник Паскаля.
Сочетания без повторений — комбинаторные соединения из n элементов по m, составленные из этих элементов и отличающиеся друг от друга только составом.:
 = n!/r!(n-r)!
Док-во
Каждомуr – сочетанию из n – элементногомн-ва соответствует r! Перестановок элементов этого сочетания. Т.о. = n!/r!(n-r)!
Док-во
Каждомуr – сочетанию из n – элементногомн-ва соответствует r! Перестановок элементов этого сочетания. Т.о.  = r! = r!  => =>  = n!/r!(n-r)!
Основныесв-ва биномиальных коэффициентов = n!/r!(n-r)!
Основныесв-ва биномиальных коэффициентов
 = =  2
2  = =  + +  3
3 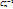 < <  Биномиальная теорема
Биномиальная теорема
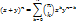
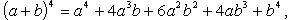
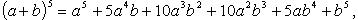
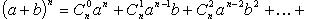
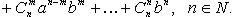 следствия
следствия
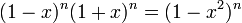

 Док-во
Док-во
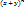 = (x+y) * … * (x+y) (n- раз)
Для того, чтобы найти указ произведнеобход из каждой скобки выбрать по одному слагаемому, перемножить их и сложить всевозможные комбинации. Получ в результате произвед = (x+y) * … * (x+y) (n- раз)
Для того, чтобы найти указ произведнеобход из каждой скобки выбрать по одному слагаемому, перемножить их и сложить всевозможные комбинации. Получ в результате произвед 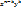 будет равно числу способов выбора из nскобок в точности kскобок, из кот при умножении и берется y. Из всех оставшихся скобок автоматически выбираются x.
Треугольник Паскаля основывается на следующем рекуррентном соотношении: будет равно числу способов выбора из nскобок в точности kскобок, из кот при умножении и берется y. Из всех оставшихся скобок автоматически выбираются x.
Треугольник Паскаля основывается на следующем рекуррентном соотношении:
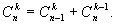
| 4 Число (r 1,..., rk) -разбиений конечного множества. Другая комбинаторная интерпретация этого числа. Полиномиальная теорема.
P(r₁ … rn) = n! / r₁! … rn!
Док-во
R₁ - элементное подмн-во S₁ можно выбрать из n – элементного мн-ва  . Для каждого из таких способов S-S₁ можно выбрать . Для каждого из таких способов S-S₁ можно выбрать  ю Делая такую выбоку для r – подмн-в мы получим: ю Делая такую выбоку для r – подмн-в мы получим:  … … 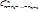 = n!/r₁!(n-r₁)! * (n-r₁)!/r₂!(n-r₁-r₂)! * … *(n-r₁ - … - = n!/r₁!(n-r₁)! * (n-r₁)!/r₂!(n-r₁-r₂)! * … *(n-r₁ - … - 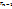 )!/ )!/  !(n-r₁ -…- !(n-r₁ -…-  )
Другая комбинаторная интерпретация этого числа
Число перестановок n-элементного мн-ва, среди кот имеется в точности )
Другая комбинаторная интерпретация этого числа
Число перестановок n-элементного мн-ва, среди кот имеется в точности  эл-тов 1ого тип и тд равно P(r₁ … rn) = n! / r₁! … rn!
Док-во
Сведем к задаче о упорялоч разбиениях. Зафикснек перестановку эл-товданногомн-ва. ПустьS={1 … n} - мн-во номеров позиций, на кот стояли эл-ты мн-ва.Обозначим через эл-тов 1ого тип и тд равно P(r₁ … rn) = n! / r₁! … rn!
Док-во
Сведем к задаче о упорялоч разбиениях. Зафикснек перестановку эл-товданногомн-ва. ПустьS={1 … n} - мн-во номеров позиций, на кот стояли эл-ты мн-ва.Обозначим через  - мн-во тех номеров позиций, но кот в нашей перестновке стояли эл-ты i-того типа. Т.о. опрупоряд разбиение ( - мн-во тех номеров позиций, но кот в нашей перестновке стояли эл-ты i-того типа. Т.о. опрупоряд разбиение (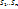 ). Между всеми перестановками заданного n- элементного мн-ва и всеми ). Между всеми перестановками заданного n- элементного мн-ва и всеми  разбиениями мн-ваSимеется биективное соответствие
Полиномиальная теорема разбиениями мн-ваSимеется биективное соответствие
Полиномиальная теорема
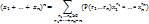 Док-во
(
Док-во
(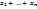 ) … ) …  Из каждой скобки мы выбираем либо
Из каждой скобки мы выбираем либо 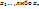 , перемножаем выбранные элементы и складываем все полученные таким образом произведения. Пусть S={1…n} – мн-во номеров скобок. Обозначим , перемножаем выбранные элементы и складываем все полученные таким образом произведения. Пусть S={1…n} – мн-во номеров скобок. Обозначим 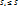 –мн-во номеров тех скобок, из которых при получении произведения берется –мн-во номеров тех скобок, из которых при получении произведения берется  . Мы получили такое разбиение, что каждому слагаемому вида . Мы получили такое разбиение, что каждому слагаемому вида 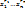 ставится в соответствие ( ставится в соответствие ( )разбиение мн-ваS. В свою очередь между всеми произведениями вида )разбиение мн-ваS. В свою очередь между всеми произведениями вида 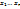 (с учетом их получения и ( (с учетом их получения и ( )разбиение мн-ваS) уст биективное соответствие. Т.о., после приведения подобных слагаемых, мы получаем, что коэффициентом явл число )разбиение мн-ваS) уст биективное соответствие. Т.о., после приведения подобных слагаемых, мы получаем, что коэффициентом явл число 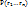
| 1 Предмет комбинатор. Логич правила комбинаторики
Комбинато́рика— раздел дискретной математики. Элементы комбинаторики - дискретные объекты, множества (сочетания, перестановки, размещения и пересечения элементов) и отношения на них (например, частичного порядка).
Основные (логические) правила.
В комбинаторном анализе есть два основных логических правила - правило суммы и правило произведения. Рассмотрим более подробно, что из себя представляет каждое из этих правил.
а) Правило суммы: Если дано два конечных множества A и B, 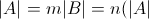 - мощность множества - мощность множества 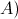 , то при , то при 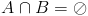 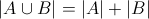 или
если некоторый выбор A можно осуществить m способами, а выбор B, отличный от A – n способами, то выбор вида «либо A, либо B» осуществить m+n – способами.
б) Правило произведения: Если A и B – конечные множества или
если некоторый выбор A можно осуществить m способами, а выбор B, отличный от A – n способами, то выбор вида «либо A, либо B» осуществить m+n – способами.
б) Правило произведения: Если A и B – конечные множества 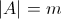 и и 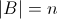 , то , то 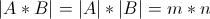 . .
| | 7 Метод «вкл и искл»(обладающих в точности t св-вами)
n(t) =  - - 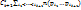 + … + + … + 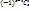 +…+ +…+ 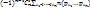 (1)
Док-во
Возьмем элемент a (1)
Док-во
Возьмем элемент a  S, который обладает не меньше, чем tсв-вами, тогда в правой части рав-ва (1) он учитывается ноль раз. Пусть элемент а обладает в точности tсв-вами S, который обладает не меньше, чем tсв-вами, тогда в правой части рав-ва (1) он учитывается ноль раз. Пусть элемент а обладает в точности tсв-вами 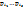 , r=t, тогда в правой части рав-ва (1) элемент а учитывается один раз. Пусть элемент а обладает больше, чем tсв-вами , r=t, тогда в правой части рав-ва (1) элемент а учитывается один раз. Пусть элемент а обладает больше, чем tсв-вами 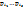 , r>t,тогда в правой части рав-ва (1) он учитывается , r>t,тогда в правой части рав-ва (1) он учитывается  раз в первом слагаемом, раз в первом слагаемом, 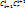 во втором и тд по аналогии: а = во втором и тд по аналогии: а =  + … + + … +  . Далее рассмотрим слагаемое . Далее рассмотрим слагаемое 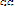 = s!/t!(s-t)!*r!/s!(r-s)! = r!/t!(s-t)!(r-s)! = [домножим и разделим на (r-t)!] = r!/t!(r-t)!*(r-t)!/(r-s)!(s-t)! = = s!/t!(s-t)!*r!/s!(r-s)! = r!/t!(s-t)!(r-s)! = [домножим и разделим на (r-t)!] = r!/t!(r-t)!*(r-t)!/(r-s)!(s-t)! = 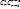 . Мы получили, что . Мы получили, что 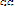 = = 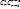 , т.е. а = , т.е. а =  + … + + … + 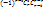 = =  ( (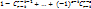 + … + + … +  ) = ) =  т.е. элемент, который обладает более, чем tсв-вами не учитывается в правой части (1), т.е эта формула справедлива для элементов, обладающих в точности tсв-вами т.е. элемент, который обладает более, чем tсв-вами не учитывается в правой части (1), т.е эта формула справедлива для элементов, обладающих в точности tсв-вами
| 14 Число Стирлинга 1ого рода
C(n,k)=C(n-1,k-1)+(n-1)C(n-1,k),
C(n,k)=0, еслиn=0 или k=0, за искл С(0,0)=1
Док-во
Для n =1 это равенство проверяется непосредственно.
Пусть перестановка (n -1)-го порядка распадается на k циклов. Число n можно добавить после любого числа в соответствующий цикл. Все полученные перестановки — различные и содержат k циклов, их количество (n -1)· s (n -1, k). Из любой перестановки (n -1)-го порядка, содержащей k -1 цикл, можно сформировать единственную перестановку n порядка, содержащую k циклов, добавив цикл образованный единственным числом n. Очевидно, что эта конструкция описывает все перестановки n -го порядка, содержащие k циклов. Тем самым равенство доказано.
| 5
Число сочетаний с повторениями
Сочетания с повторениями — комбинаторные соединения из n элементов по m, составленные из этих элементов без учета порядка с возможностью многократного повторения предметов.:
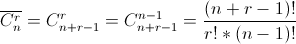 Док-во
Строим k-сочетания с повторениями из элементногомн-ваS={
Док-во
Строим k-сочетания с повторениями из элементногомн-ваS={ 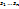 }.В каждом таком наборе сначала расположим элементы типа }.В каждом таком наборе сначала расположим элементы типа  , затем типа , затем типа  ,и так далее. Каждому k-сочетанию с повторениями поставим в соответствие последовательность из 0 и 1 длины n+k-1, число единиц в этой последовательности равно k, число нулей n-1. Каждый 0 отделяет наборы различных типов. Каждое k-сочетание с повторениями однозначно определяет указанную последовательность и наоборот. Т.к. количество упорядоченных наборов из 0 и 1 длины n, состоящих из k единиц равно ,и так далее. Каждому k-сочетанию с повторениями поставим в соответствие последовательность из 0 и 1 длины n+k-1, число единиц в этой последовательности равно k, число нулей n-1. Каждый 0 отделяет наборы различных типов. Каждое k-сочетание с повторениями однозначно определяет указанную последовательность и наоборот. Т.к. количество упорядоченных наборов из 0 и 1 длины n, состоящих из k единиц равно  , тотаких последовательностей существует , тотаких последовательностей существует 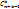 . Значит, . Значит,  = = 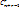
| 6
Метод «вкл и искл» (не обладающих св-вами)
n(0) = n –  + + 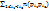 - … - - … -  + … + + … + 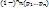 Док-во
Элемент мн-ваS,кот не обладает ни одним из св-в (
Док-во
Элемент мн-ваS,кот не обладает ни одним из св-в (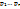 ) в левой части рав-ва учитывается 1 раз, в правой части рав-ва так же один раз, а именно в первом слагаемом. Пусть теперь a ) в левой части рав-ва учитывается 1 раз, в правой части рав-ва так же один раз, а именно в первом слагаемом. Пусть теперь a  S – элемент, который обладает св-вами, тогда 1-r + S – элемент, который обладает св-вами, тогда 1-r +  - -  + … + + … + 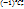 +.. + +.. + 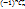
| |
8
Примен. метода вкл. и искл. (задача о бесп., задача о числе сюръект. отобр.)
Задача о беспорядках
Требуется найти число перестановок 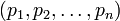 множества множества 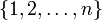 таких что таких что 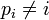 для всех i. Такие перестановки называются беспорядками.
Пусть для всех i. Такие перестановки называются беспорядками.
Пусть 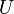 — множество всех перестановок — множество всех перестановок 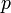 и пусть свойство и пусть свойство 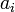 перестановки выражается равенством перестановки выражается равенством 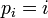 . Тогда число беспорядков есть . Тогда число беспорядков есть 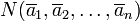 . Легко видеть, что . Легко видеть, что 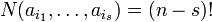 — число перестановок, оставляющих на месте элементы — число перестановок, оставляющих на месте элементы 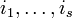 , и таким образом сумма , и таким образом сумма 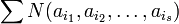 содержит содержит 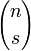 одинаковых слагаемых. Формула включений-исключений дает выражение для числа одинаковых слагаемых. Формула включений-исключений дает выражение для числа 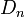 беспорядков: беспорядков:
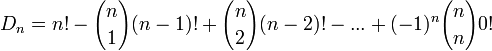 Это соотношение можно преобразовать к виду
Это соотношение можно преобразовать к виду
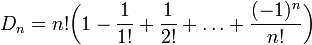 Нетрудно видеть, что выражение в скобках является частичной суммой ряда
Нетрудно видеть, что выражение в скобках является частичной суммой ряда 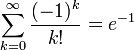 . Таким образом, с хорошей точностью число беспорядков составляет . Таким образом, с хорошей точностью число беспорядков составляет 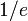 долю от общего числа долю от общего числа 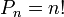 перестановок: перестановок:
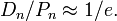 Число сюръективных отображений конечного
множества X; |X|= n, на конечное множество Y; |Y | = m, то
есть число функций f:XàY, таких, что f (X) = Y,
равно cогласно принципу включения-исключения:
f(n,m) =
Число сюръективных отображений конечного
множества X; |X|= n, на конечное множество Y; |Y | = m, то
есть число функций f:XàY, таких, что f (X) = Y,
равно cогласно принципу включения-исключения:
f(n,m) =  + + 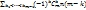 ^n = ^n =  + + 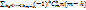 ^n
15.
Упорядоченные и неупорядоченные разбиения множеств. Число Стирлинга 2-го рода. Формула и рекуррентное соотношение для числа Стирлинга 2-го рода.
число Стирлинга второго рода ^n
15.
Упорядоченные и неупорядоченные разбиения множеств. Число Стирлинга 2-го рода. Формула и рекуррентное соотношение для числа Стирлинга 2-го рода.
число Стирлинга второго рода 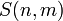 представляет собой количество неупорядоченных разбиений n -элементного множества на m частей, в то время какмультиномиальный коэффициент представляет собой количество неупорядоченных разбиений n -элементного множества на m частей, в то время какмультиномиальный коэффициент 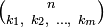 выражает количество упорядоченных разбиений n -элементного множества на m частей фиксированного размера выражает количество упорядоченных разбиений n -элементного множества на m частей фиксированного размера 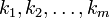 . Количество всех неупорядоченных разбиений n -элементного множества задается числом Белла . Количество всех неупорядоченных разбиений n -элементного множества задается числом Белла 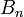 .
Числом Стирлинга второго рода из n по k, обозначаемым .
Числом Стирлинга второго рода из n по k, обозначаемым 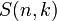 или или 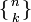 , называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
Числа Стирлинга второго рода удовлетворяют рекуррентному соотношению: , называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
Числа Стирлинга второго рода удовлетворяют рекуррентному соотношению:
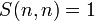 , для n ≥ 0, , для n ≥ 0,
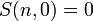 , для n > 0, , для n > 0,
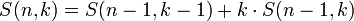 для для 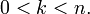
| 9
Понятие рекуррентного соотношения. Рекуррентное соотношение k -го порядка дляфункции одной переменной, его общее решение.
Рекуррентно e соотношени e - соотношение между элементами последовательности, в которой следующий элемент выражается через несколько предыдущий.
Рекурентная формула — формула вида 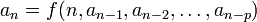 , выражающая каждый член последовательности , выражающая каждый член последовательности 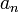 через p предыдущих членов. Например - числа Фибоначчи через p предыдущих членов. Например - числа Фибоначчи 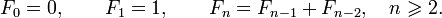 Линейным рекуррентным соотношением k - го порядка(k - фиксировано) с постоянными коэффициентами называется рекуррентное соотношение следующего вида:
Линейным рекуррентным соотношением k - го порядка(k - фиксировано) с постоянными коэффициентами называется рекуррентное соотношение следующего вида:
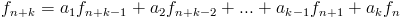 (3) (3)
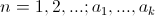 - постоянные - постоянные 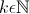 .
Характеристическим уравнением рекуррентного соотношения (3) является уравнение вида .
Характеристическим уравнением рекуррентного соотношения (3) является уравнение вида
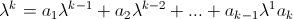 Теорема 2: Пусть
Теорема 2: Пусть  - все попарно различные корни характеристического уравнения рекурретного соотношения (3) - все попарно различные корни характеристического уравнения рекурретного соотношения (3) 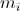 - кратность корня - кратность корня 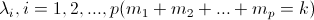 . Тогда общее решение рекуррентного соотношения (3) имеет следующий вид: . Тогда общее решение рекуррентного соотношения (3) имеет следующий вид:
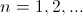 . . 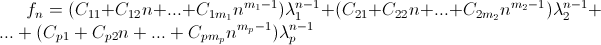 В частности, если
В частности, если 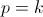 , то , то
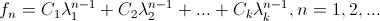 12
Общее решение линейного неоднородного рекуррентного соотношения с постоянными коэффициентами
Общее решение неоднородного рекурентного соотношения есть сумма общего решения однородного соотношения и какого-либо решения из неоднородных рекурентных соотношений.
Док-во
Пусть (
12
Общее решение линейного неоднородного рекуррентного соотношения с постоянными коэффициентами
Общее решение неоднородного рекурентного соотношения есть сумма общего решения однородного соотношения и какого-либо решения из неоднородных рекурентных соотношений.
Док-во
Пусть ( )-нек решение неоднордного соотнош, а ( )-нек решение неоднордного соотнош, а (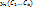 )-общее решоднороднсоотнош. Необход док-ть, что ( )-общее решоднороднсоотнош. Необход док-ть, что (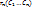 ) = ) = 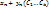 -общее решнеоднорднсоотнош. -общее решнеоднорднсоотнош. 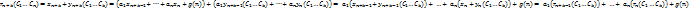 Мы доказали, что Мы доказали, что 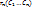 явл решение неоднородн соотнош. Теперь необход показать, что оно явл общим. Для этого необход док-ть, что явл решение неоднородн соотнош. Теперь необход показать, что оно явл общим. Для этого необход док-ть, что  решения неоднород соотнош сущ-т решения неоднород соотнош сущ-т 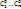 , что посл-сть ( , что посл-сть ( )уд неоднородсоотнош. Для этого запишем )уд неоднородсоотнош. Для этого запишем 
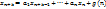 Вычитаем одно из 2ого и получаем:
Вычитаем одно из 2ого и получаем:
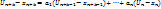 Т.о. получаем, что ( Т.о. получаем, что ( ) – общее реш однородного соотнош, т.к. сущ-т общее реш неоднород соотнош ) – общее реш однородного соотнош, т.к. сущ-т общее реш неоднород соотнош 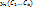 , то по опр сущ-т , то по опр сущ-т 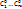 такое, что такое, что 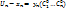 , т.е. вып-тся , т.е. вып-тся 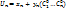 => => 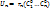
| 10
Общее решение линейного однородного рекуррентного соотношения с постоянными коэффициентами.
Пусть характеристическое ур-ние рекуррентного соотношения имеет р парно различных корней: 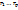 крастностей соответственно крастностей соответственно 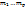 , тогда посл-сть ( , тогда посл-сть (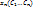 )явл общим решением, где )явл общим решением, где 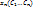 = = 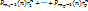 , где , где 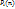 - мн-н степени не выше i, завис от n
Док-во
Поскольку - мн-н степени не выше i, завис от n
Док-во
Поскольку  явл корнем характеристического ур-ния рекур соотнош, значит каждая посл-ть ( явл корнем характеристического ур-ния рекур соотнош, значит каждая посл-ть ( ) явл решение рекурсоотнош. Докажем теор для случая када кратность корней равна 1. Тогда рав-во можно переписать виде: ) явл решение рекурсоотнош. Докажем теор для случая када кратность корней равна 1. Тогда рав-во можно переписать виде: 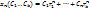 , p=k. Следвательнолин комбинация( , p=k. Следвательнолин комбинация( )так же явл решением рекурсоотнош. Др словами, посл-сть ( )так же явл решением рекурсоотнош. Др словами, посл-сть (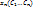 ) с мн-ном ) с мн-ном  – решение рекур соотнош
Необход д-ть, что эти решения будут общими,т.е. необход, чтобы – решение рекур соотнош
Необход д-ть, что эти решения будут общими,т.е. необход, чтобы 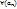 сущ-ли сущ-ли 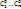 , такие, что , такие, что 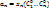 . Рассмотрим
при n=0: . Рассмотрим
при n=0: 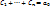 ,
при n=1: ,
при n=1: 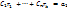 …
при n=k-1:
…
при n=k-1:  = = 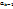 Получ система ур-ний из kур-ний с неизвестными
Получ система ур-ний из kур-ний с неизвестными  , относ кот нужно выяснить имеет ли реш данная система. Опр данной системы будет явл , относ кот нужно выяснить имеет ли реш данная система. Опр данной системы будет явл
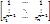 = = 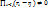 Т.о. мы получили, что ранг матрицы данной системы равен рангу рассмотр матрицы, значит даннай система совместима, а это означ, что сущ-т решение
Т.о. мы получили, что ранг матрицы данной системы равен рангу рассмотр матрицы, значит даннай система совместима, а это означ, что сущ-т решение  13
Разбиение подстановки на циклы. Число подстановок n -элементного множества, имеющих предписанных циклический тип.
Циклом длины lназ. такая подстановка а конечного множества Y={y1,..., у l ], что ш
13
Разбиение подстановки на циклы. Число подстановок n -элементного множества, имеющих предписанных циклический тип.
Циклом длины lназ. такая подстановка а конечного множества Y={y1,..., у l ], что ш
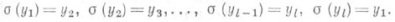 Конечный цикл обозначается (y1, y2,..., yl). Бесконечным циклом наз. такая П. счетного множества
Конечный цикл обозначается (y1, y2,..., yl). Бесконечным циклом наз. такая П. счетного множества
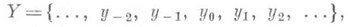 что для любого целого i s(yi)= yi+1 Обозначение бесконечного цикла таково:
что для любого целого i s(yi)= yi+1 Обозначение бесконечного цикла таково:
 Цикл длины 2 есть транспозиция. Группа Sn содержит (п- 1)! циклов длины п. Для любой подстановки g из S(X).существует такое разбиение множества X на непересекающиеся подмножества, что на каждом из них g действует как цикл. Конечные подмножества этого разбиения имеют вид
Цикл длины 2 есть транспозиция. Группа Sn содержит (п- 1)! циклов длины п. Для любой подстановки g из S(X).существует такое разбиение множества X на непересекающиеся подмножества, что на каждом из них g действует как цикл. Конечные подмножества этого разбиения имеют вид
 где g l (x}=x, а бесконечные -
где g l (x}=x, а бесконечные -
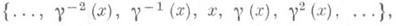
| 11
Числа Фибоначчи. Вывод формулы n-го числа Фибоначчи решением линейного
однородного рекуррентного соотношения 2-го порядка.
Линейным однородным рекуррентным соотношением второго порядка с постоянными коэффициентами называется рекуррентное соотношение вида:
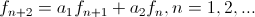 (2) (2)
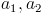 - нейкие коэффициенты, причем - нейкие коэффициенты, причем 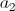 отлично от нуля. Уравнение вида отлично от нуля. Уравнение вида
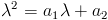 - характеристическое уравнение рекуррентного соотношения (2).
Теорема 1: Если характеристическое уравнение рекуррентного соотношения (2) имеет два различных корня - характеристическое уравнение рекуррентного соотношения (2).
Теорема 1: Если характеристическое уравнение рекуррентного соотношения (2) имеет два различных корня 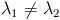 , то общее решение рекуррентного соотношения (2) имеет вид , то общее решение рекуррентного соотношения (2) имеет вид
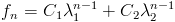 Если рекуррентное соотношение имеет два равных корня
Если рекуррентное соотношение имеет два равных корня 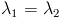 , то общее решение рекуррентного соотношения (2) имеет следующий вид , то общее решение рекуррентного соотношения (2) имеет следующий вид
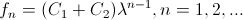 последовательность чисел Фибоначчи
последовательность чисел Фибоначчи 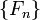 задается линейным рекуррентным соотношением: задается линейным рекуррентным соотношением: 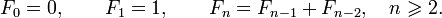 14 Число Стирлинга 1ого рода
Числа Стирлинга первого рода (без знака) — количество перестановок порядка n с k циклами.
Числами Стирлинга первого рода (со знаком) s(n, k) называются коэффициенты многочлена:
14 Число Стирлинга 1ого рода
Числа Стирлинга первого рода (без знака) — количество перестановок порядка n с k циклами.
Числами Стирлинга первого рода (со знаком) s(n, k) называются коэффициенты многочлена:
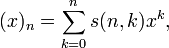 где
где 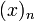 — символ Похгаммера (убывающий факториал): — символ Похгаммера (убывающий факториал):
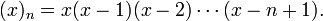 Как видно из определения, числа имеют чередующийся знак. Их абсолютные значения задают количество перестановок множества, состоящего из n элементов с k циклами.
Числа Стирлинга первого рода задаются рекуррентным соотношением:
Как видно из определения, числа имеют чередующийся знак. Их абсолютные значения задают количество перестановок множества, состоящего из n элементов с k циклами.
Числа Стирлинга первого рода задаются рекуррентным соотношением:
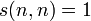 , для n ≥ 0, , для n ≥ 0,
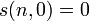 , для n > 0, , для n > 0,
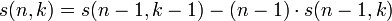 для для 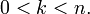 Док-во
Для n =1 это равенство проверяется непосредственно. Пусть перестановка (n -1)-го порядка распадается на k циклов. Число n можно добавить после любого числа в соответствующий цикл. Все полученные перестановки различны и содержат k циклов, их количество (n -1)· s (n -1, k). Из любой перестановки (n -1)-го порядка, содержащей k -1 цикл, можно сформировать единственную перестановку n порядка, содержащую k циклов, добавив цикл образованный единственным числом n. Очевидно, что эта конструкция описывает все перестановки n -го порядка, содержащие k циклов. Тем самым равенство доказано.
Док-во
Для n =1 это равенство проверяется непосредственно. Пусть перестановка (n -1)-го порядка распадается на k циклов. Число n можно добавить после любого числа в соответствующий цикл. Все полученные перестановки различны и содержат k циклов, их количество (n -1)· s (n -1, k). Из любой перестановки (n -1)-го порядка, содержащей k -1 цикл, можно сформировать единственную перестановку n порядка, содержащую k циклов, добавив цикл образованный единственным числом n. Очевидно, что эта конструкция описывает все перестановки n -го порядка, содержащие k циклов. Тем самым равенство доказано.
| |
28 Полиномиальная нормальная форма. Полином Жегалкина. Теорема о единственности представления булевой функции посредством полинома Жегалкина
Под полиномом булевой функции понимаем сложение по модулю два конечного множества элементарных конъюнкций. Степенью полинома является наибольший ранг элементарной конъюнкции, входящей в этот полином.
Полином, содержащий все переменные без знака отрицания, называется полиномом Жегалкина.
Для каждой булевой функции существует единственный полином Жегалкина, реализующий эту функцию.
 ={0;1}, ={0;1},  -двоичное представление числа k, -двоичное представление числа k, 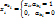 7
Теор о ед-сти представ бул ф-циипоср-ом п.Жегалкина
Для любой булевой ф-циисущ-т в точности один полином Жегалкина.
Док-во
f=f( 7
Теор о ед-сти представ бул ф-циипоср-ом п.Жегалкина
Для любой булевой ф-циисущ-т в точности один полином Жегалкина.
Док-во
f=f(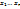 ), a(f)=( ), a(f)=(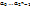 ). Каждый полином Жегалкина однозначно определяется вектором ( ). Каждый полином Жегалкина однозначно определяется вектором (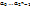 ). Векторов ( ). Векторов (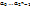 ) будет сущ-ть в точности ) будет сущ-ть в точности 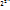 , а это число всех булевых функций от n переменных, т.е каждой функции соответствует свой полином Жегалкина , а это число всех булевых функций от n переменных, т.е каждой функции соответствует свой полином Жегалкина
| 29
Замкнутые классы булевых ф-ций
Замкнутый класс в теории булевых функций — такое множество 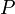 функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: 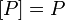 . Другими словами, любая функция, которую можно выразить формулой с использованием функций множества . Другими словами, любая функция, которую можно выразить формулой с использованием функций множества 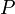 , снова входит в это же множество.
1. Класс , снова входит в это же множество.
1. Класс  - сохрconst 0 – явлзамкнутым
Док-во
Пусть ф-цииg=g( - сохрconst 0 – явлзамкнутым
Док-во
Пусть ф-цииg=g(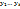 ) и ) и  =f( =f(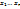 ) ) 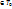 . Пусть h-суперпозиция. Рассмотрим h=h(0, … 0) = g( . Пусть h-суперпозиция. Рассмотрим h=h(0, … 0) = g(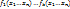 ) = g(0, … 0) = 0
2. Класс ) = g(0, … 0) = 0
2. Класс  - сохрconst 1 – явлзамкнутым
Док-воаналогичное
3. Класс - сохрconst 1 – явлзамкнутым
Док-воаналогичное
3. Класс  –самодвойственная ф-ция – явл замкнутым
Док-во
Пусть ф-цииg=g( –самодвойственная ф-ция – явл замкнутым
Док-во
Пусть ф-цииg=g(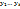 ) и ) и  =f( =f(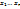 ) ) 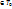 . Пусть h-суперпозиция. Рассмотрим h( . Пусть h-суперпозиция. Рассмотрим h( ) = g( ) = g(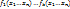 ) = g( ) = g(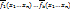 ) = ) =  ( (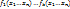 ) = ) =  ( (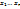 )
4. Класс )
4. Класс  –монотонная ф-ция – явл замкнутым
Док-во –монотонная ф-ция – явл замкнутым
Док-во
 = ( = ( )и )и  = ( = ( ) )  {0,1}. Пусть ф-цииg=g( {0,1}. Пусть ф-цииg=g(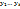 ) и ) и  =f( =f(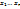 ) ) 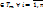 . Пусть h-суперпозиция. Скажем, что . Пусть h-суперпозиция. Скажем, что 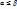 . h( . h( ) = g( ) = g(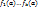 ) )  g( g(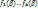 ) = h( ) = h( )
5. Класс )
5. Класс  –линейная ф-ция – явл замкнутым
Док-во
Т.к. суперпозиция полинома Жегалкина степени не выше 1 так же явл полиномом степени не выше 1. –линейная ф-ция – явл замкнутым
Док-во
Т.к. суперпозиция полинома Жегалкина степени не выше 1 так же явл полиномом степени не выше 1.
| 30 Полнота системы булевых функций. Теорема Поста (без доказательства).
Множество  функций алгебры логики называется полной системой, если замыкание этого множества совпадает с множеством всех функций. (В частности, для двузначной логики функций алгебры логики называется полной системой, если замыкание этого множества совпадает с множеством всех функций. (В частности, для двузначной логики 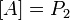 .) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества .) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества  .
Теорема Поста
Система булевых функций F является полной тогда и только тогда, когда она не содержится ни в одном из классов .
Теорема Поста
Система булевых функций F является полной тогда и только тогда, когда она не содержится ни в одном из классов 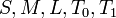 , т.е. когда в ней имеется хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция , т.е. когда в ней имеется хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция
| 27
Алгоритм Квайна нахождения минимальной ДНФ булевой функции.
(теорема Квайна). Если в СДНФ в начале произвести все операции неполного склеивания, а затем все операции поглощения, то в результате получится сокращенная ДНФ.
Покажем, что, применяя операцию неполного склеивания, получим все простые импликанты функции. Введем операцию развертывания, которая обратна операции склеивания: это есть умножение каждого произведения на выражение вида 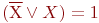 .
Пусть .
Пусть 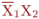 – простая импликанта некоторой – простая импликанта некоторой 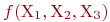 трех переменных. Тогда: трех переменных. Тогда:
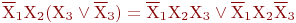 получатся после многократного применения этой операции дизъюнкции конституент единицы исходной функции, т.е. ее СДНФ.
получатся после многократного применения этой операции дизъюнкции конституент единицы исходной функции, т.е. ее СДНФ.
| |
16
Число Белла. Рекуррентное соотношение для числа Белла.
числом Белла 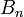 называется число всех неупорядоченных разбиений n -элементного множества, при этом по определению полагают называется число всех неупорядоченных разбиений n -элементного множества, при этом по определению полагают 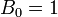 .
Числа Белла можно задать в рекуррентном виде: .
Числа Белла можно задать в рекуррентном виде:
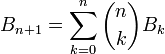 .
Число Белла можно вычислить как сумму чисел Стирлинга второго рода: .
Число Белла можно вычислить как сумму чисел Стирлинга второго рода:
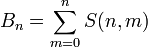 20
Теорема Рамсея.
Пусть
20
Теорема Рамсея.
Пусть 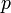 , ,  и и  — натуральные числа, причем — натуральные числа, причем 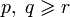 . Тогда существует число . Тогда существует число 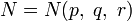 , обладающее следующим свойством: если все , обладающее следующим свойством: если все  -элементные подмножества -элементные подмножества  -элементного множества -элементного множества 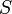 произвольным образом разбиты на два непересекающихся семейства произвольным образом разбиты на два непересекающихся семейства 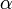 и и 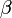 , то либо существует , то либо существует 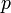 -элементное подмножество множества -элементное подмножество множества 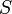 , все , все  -элементные подмножества которого содержатся в -элементные подмножества которого содержатся в 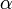 , либо существует , либо существует  -элементное подмножество, все -элементное подмножество, все  -элементные подмножества которого содержатся в -элементные подмножества которого содержатся в 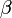 . .
| 17
Упорядоченные и неупорядоченные разбиения чисел. Рекуррентные соотношения для количества неупорядоченных разбиений натурального числа на фиксированное число слагаемых.
Разбие́ние числа́ n — это представление n в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие откомпозиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В канонической записи разбиения части перечисляются в невозрастающем порядке.
Количество разбиений числа n на слагаемые, используя числа не превышающие k: 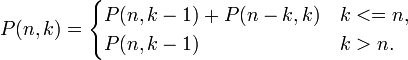 Количество разбиений натурального числа n на k слагаемых:
Количество разбиений натурального числа n на k слагаемых: 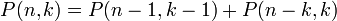 21
Булевы функции. Способы их задания. Число бул. Ф-ий от n переменных.
Логической (булевой) функцией (или просто функцией) n переменных y = f(x 1, x 2, …, xn) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.
Кол-во бул.ф-ий 2^(2^ n)
1. Табличный
21
Булевы функции. Способы их задания. Число бул. Ф-ий от n переменных.
Логической (булевой) функцией (или просто функцией) n переменных y = f(x 1, x 2, …, xn) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.
Кол-во бул.ф-ий 2^(2^ n)
1. Табличный

| 18
Система различных представителей. Теорема Холла (без доказательства).
Система различных представителей для семейтсва конечных множеств S = {A1, A2,..,Ai,…,Am} есть система попарно различных элементов {a1, a2,…, ai,…, am}, для которых ai ∈Ai [i=1,2…m].
Теорема Холла:
Пусть задано мн-во S, задан набор (необязательно различных) подмн-в из ST=( ). Тогда для Т сущ-т система различных представителей такая, что ). Тогда для Т сущ-т система различных представителей такая, что  и и  подмн-ва { подмн-ва {  } }  [m] вып-тся условие: | [m] вып-тся условие: |  | |  k k
22
Док-во
1. Необходимость очевидна. Пусть для (1) сущ-т система общих представителей, мн-во 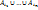 сод-т kэл-товмн-ва С. Учитывая вкл сод-т kэл-товмн-ва С. Учитывая вкл 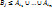 эл-тов долно быть больше, чем k?! эл-тов долно быть больше, чем k?!
2. Достаточность. S’={ 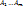 }. Рассмотрим набор Тподмн-вамн-ваS’. T=( }. Рассмотрим набор Тподмн-вамн-ваS’. T=( ), где ), где  ={ ={ 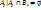 }. Если взять i=1, то получается, что }. Если взять i=1, то получается, что 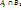 … при i=m: … при i=m: 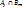 . РокажемЮч то для Т сущ-т система различных представителей (теор Холла) . РокажемЮч то для Т сущ-т система различных представителей (теор Холла) 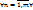 подмн-ва { подмн-ва {  } }  [m] вып-тся условие: | [m] вып-тся условие: |  | |  k. Преположим, что это не выполняется, тогда должно сущ-тьnи такое подмн-во { k. Преположим, что это не выполняется, тогда должно сущ-тьnи такое подмн-во {  }, что }, что  | |  k, т.е. н-во k, т.е. н-во  ={ ={  }?! Покажем, что мн-во }?! Покажем, что мн-во 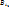 c c  а а  не сод-т не сод-т 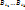 , значит для набора Т сущ-т система различных представителей. Выберем в , значит для набора Т сущ-т система различных представителей. Выберем в 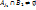 c c  аналогично и для аналогично и для 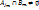 c c  . Получим С={ . Получим С={  … …  }, т.е. систему различных представителей }, т.е. систему различных представителей
23
Число всех подмн-в n -элементного множества
|B(S)| = 2ⁿ
Док-во
Даны А и В, причем число элементов А задано и сущ-т биекция φ: A->B, тогда |B| = |A|
АсS, A->  = (x₁ x₂ … xn), xi= 1, если принадлежит и 0, если иначе. Φ – мн-во всех бинарных посл-тей длины 2. Т.к. отображение φ – биективно{0;1} => = (x₁ x₂ … xn), xi= 1, если принадлежит и 0, если иначе. Φ – мн-во всех бинарных посл-тей длины 2. Т.к. отображение φ – биективно{0;1} =>  = 2ⁿ. = 2ⁿ.
| 3 Число r -сочетаний из n элементов. Биномиальнаятеорема и следствия из нее. Основны e свойства биномиальных коэффициентов. Треугольник Паскаля.
Сочетания без повторений — комбинаторные соединения из n элементов по m, составленные из этих элементов и отличающиеся друг от друга только составом.:
 = n!/r!(n-r)!
Док-во
Каждомуr – сочетанию из n – элементногомн-ва соответствует r! Перестановок элементов этого сочетания. Т.о. = n!/r!(n-r)!
Док-во
Каждомуr – сочетанию из n – элементногомн-ва соответствует r! Перестановок элементов этого сочетания. Т.о.  = r! = r!  => =>  = n!/r!(n-r)!
Основныесв-ва биномиальных коэффициентов = n!/r!(n-r)!
Основныесв-ва биномиальных коэффициентов
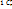 = = 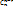 2
2  = = 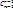 + + 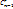 3
3 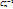 < <  Биномиальная теорема
Биномиальная теорема
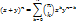
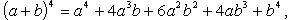
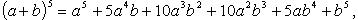

|
|
|
|



 = (x₁ x₂ … xn), xi= 1, если принадлежит и 0, если иначе. Φ – мн-во всех бинарных посл-тей длины 2. Т.к. отображение φ – биективно{0;1} =>
= (x₁ x₂ … xn), xi= 1, если принадлежит и 0, если иначе. Φ – мн-во всех бинарных посл-тей длины 2. Т.к. отображение φ – биективно{0;1} =>  = 2ⁿ.
= 2ⁿ. = n!/r!(n-r)!
Док-во
Каждомуr – сочетанию из n – элементногомн-ва соответствует r! Перестановок элементов этого сочетания. Т.о.
= n!/r!(n-r)!
Док-во
Каждомуr – сочетанию из n – элементногомн-ва соответствует r! Перестановок элементов этого сочетания. Т.о.  = r!
= r! 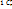 =
= 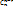 2
2 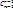 +
+ 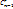 3
3 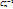 <
<  Биномиальная теорема
Биномиальная теорема
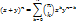
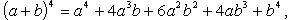
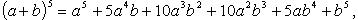
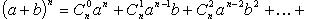
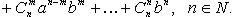 следствия
следствия
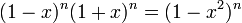

 Док-во
Док-во
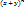 = (x+y) * … * (x+y) (n- раз)
Для того, чтобы найти указ произведнеобход из каждой скобки выбрать по одному слагаемому, перемножить их и сложить всевозможные комбинации. Получ в результате произвед
= (x+y) * … * (x+y) (n- раз)
Для того, чтобы найти указ произведнеобход из каждой скобки выбрать по одному слагаемому, перемножить их и сложить всевозможные комбинации. Получ в результате произвед 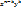 будет равно числу способов выбора из nскобок в точности kскобок, из кот при умножении и берется y. Из всех оставшихся скобок автоматически выбираются x.
Треугольник Паскаля основывается на следующем рекуррентном соотношении:
будет равно числу способов выбора из nскобок в точности kскобок, из кот при умножении и берется y. Из всех оставшихся скобок автоматически выбираются x.
Треугольник Паскаля основывается на следующем рекуррентном соотношении:
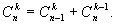
 . Для каждого из таких способов S-S₁ можно выбрать
. Для каждого из таких способов S-S₁ можно выбрать 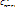 ю Делая такую выбоку для r – подмн-в мы получим:
ю Делая такую выбоку для r – подмн-в мы получим: 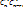 …
… 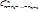 = n!/r₁!(n-r₁)! * (n-r₁)!/r₂!(n-r₁-r₂)! * … *(n-r₁ - … -
= n!/r₁!(n-r₁)! * (n-r₁)!/r₂!(n-r₁-r₂)! * … *(n-r₁ - … - 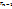 )!/
)!/  !(n-r₁ -…-
!(n-r₁ -…-  эл-тов 1ого тип и тд равно P(r₁ … rn) = n! / r₁! … rn!
Док-во
Сведем к задаче о упорялоч разбиениях. Зафикснек перестановку эл-товданногомн-ва. ПустьS={1 … n} - мн-во номеров позиций, на кот стояли эл-ты мн-ва.Обозначим через
эл-тов 1ого тип и тд равно P(r₁ … rn) = n! / r₁! … rn!
Док-во
Сведем к задаче о упорялоч разбиениях. Зафикснек перестановку эл-товданногомн-ва. ПустьS={1 … n} - мн-во номеров позиций, на кот стояли эл-ты мн-ва.Обозначим через  - мн-во тех номеров позиций, но кот в нашей перестновке стояли эл-ты i-того типа. Т.о. опрупоряд разбиение (
- мн-во тех номеров позиций, но кот в нашей перестновке стояли эл-ты i-того типа. Т.о. опрупоряд разбиение (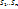 ). Между всеми перестановками заданного n- элементного мн-ва и всеми
). Между всеми перестановками заданного n- элементного мн-ва и всеми 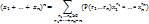 Док-во
(
Док-во
(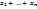 ) …
) …  Из каждой скобки мы выбираем либо
Из каждой скобки мы выбираем либо 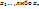 , перемножаем выбранные элементы и складываем все полученные таким образом произведения. Пусть S={1…n} – мн-во номеров скобок. Обозначим
, перемножаем выбранные элементы и складываем все полученные таким образом произведения. Пусть S={1…n} – мн-во номеров скобок. Обозначим 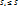 –мн-во номеров тех скобок, из которых при получении произведения берется
–мн-во номеров тех скобок, из которых при получении произведения берется  . Мы получили такое разбиение, что каждому слагаемому вида
. Мы получили такое разбиение, что каждому слагаемому вида 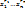 ставится в соответствие (
ставится в соответствие ( )разбиение мн-ваS. В свою очередь между всеми произведениями вида
)разбиение мн-ваS. В свою очередь между всеми произведениями вида 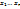 (с учетом их получения и (
(с учетом их получения и (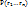
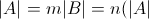 - мощность множества
- мощность множества 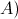 , то при
, то при 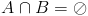
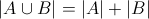 или
если некоторый выбор A можно осуществить m способами, а выбор B, отличный от A – n способами, то выбор вида «либо A, либо B» осуществить m+n – способами.
б) Правило произведения: Если A и B – конечные множества
или
если некоторый выбор A можно осуществить m способами, а выбор B, отличный от A – n способами, то выбор вида «либо A, либо B» осуществить m+n – способами.
б) Правило произведения: Если A и B – конечные множества 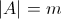 и
и 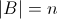 , то
, то 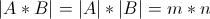 .
.
 -
- 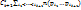 + … +
+ … + 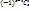 +…+
+…+ 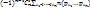 (1)
Док-во
Возьмем элемент a
(1)
Док-во
Возьмем элемент a  S, который обладает не меньше, чем tсв-вами, тогда в правой части рав-ва (1) он учитывается ноль раз. Пусть элемент а обладает в точности tсв-вами
S, который обладает не меньше, чем tсв-вами, тогда в правой части рав-ва (1) он учитывается ноль раз. Пусть элемент а обладает в точности tсв-вами 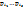 , r=t, тогда в правой части рав-ва (1) элемент а учитывается один раз. Пусть элемент а обладает больше, чем tсв-вами
, r=t, тогда в правой части рав-ва (1) элемент а учитывается один раз. Пусть элемент а обладает больше, чем tсв-вами  раз в первом слагаемом,
раз в первом слагаемом, 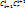 во втором и тд по аналогии: а =
во втором и тд по аналогии: а =  + … +
+ … +  . Далее рассмотрим слагаемое
. Далее рассмотрим слагаемое 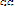 = s!/t!(s-t)!*r!/s!(r-s)! = r!/t!(s-t)!(r-s)! = [домножим и разделим на (r-t)!] = r!/t!(r-t)!*(r-t)!/(r-s)!(s-t)! =
= s!/t!(s-t)!*r!/s!(r-s)! = r!/t!(s-t)!(r-s)! = [домножим и разделим на (r-t)!] = r!/t!(r-t)!*(r-t)!/(r-s)!(s-t)! = 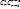 . Мы получили, что
. Мы получили, что  + … +
+ … + 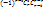 =
= 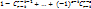 + … +
+ … +  ) =
) =  т.е. элемент, который обладает более, чем tсв-вами не учитывается в правой части (1), т.е эта формула справедлива для элементов, обладающих в точности tсв-вами
т.е. элемент, который обладает более, чем tсв-вами не учитывается в правой части (1), т.е эта формула справедлива для элементов, обладающих в точности tсв-вами
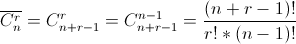 Док-во
Строим k-сочетания с повторениями из элементногомн-ваS={
Док-во
Строим k-сочетания с повторениями из элементногомн-ваS={ 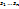 }.В каждом таком наборе сначала расположим элементы типа
}.В каждом таком наборе сначала расположим элементы типа  , затем типа
, затем типа  ,и так далее. Каждому k-сочетанию с повторениями поставим в соответствие последовательность из 0 и 1 длины n+k-1, число единиц в этой последовательности равно k, число нулей n-1. Каждый 0 отделяет наборы различных типов. Каждое k-сочетание с повторениями однозначно определяет указанную последовательность и наоборот. Т.к. количество упорядоченных наборов из 0 и 1 длины n, состоящих из k единиц равно
,и так далее. Каждому k-сочетанию с повторениями поставим в соответствие последовательность из 0 и 1 длины n+k-1, число единиц в этой последовательности равно k, число нулей n-1. Каждый 0 отделяет наборы различных типов. Каждое k-сочетание с повторениями однозначно определяет указанную последовательность и наоборот. Т.к. количество упорядоченных наборов из 0 и 1 длины n, состоящих из k единиц равно  , тотаких последовательностей существует
, тотаких последовательностей существует 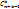 . Значит,
. Значит,  =
= 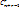
 +
+ 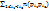 - … -
- … -  + … +
+ … + 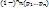 Док-во
Элемент мн-ваS,кот не обладает ни одним из св-в (
Док-во
Элемент мн-ваS,кот не обладает ни одним из св-в (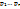 ) в левой части рав-ва учитывается 1 раз, в правой части рав-ва так же один раз, а именно в первом слагаемом. Пусть теперь a
) в левой части рав-ва учитывается 1 раз, в правой части рав-ва так же один раз, а именно в первом слагаемом. Пусть теперь a  -
-  + … +
+ … + 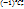 +.. +
+.. + 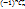
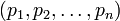 множества
множества 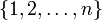 таких что
таких что 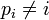 для всех i. Такие перестановки называются беспорядками.
Пусть
для всех i. Такие перестановки называются беспорядками.
Пусть 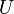 — множество всех перестановок
— множество всех перестановок 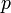 и пусть свойство
и пусть свойство 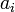 перестановки выражается равенством
перестановки выражается равенством 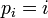 . Тогда число беспорядков есть
. Тогда число беспорядков есть 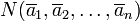 . Легко видеть, что
. Легко видеть, что 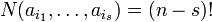 — число перестановок, оставляющих на месте элементы
— число перестановок, оставляющих на месте элементы 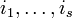 , и таким образом сумма
, и таким образом сумма 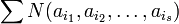 содержит
содержит 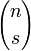 одинаковых слагаемых. Формула включений-исключений дает выражение для числа
одинаковых слагаемых. Формула включений-исключений дает выражение для числа 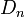 беспорядков:
беспорядков:
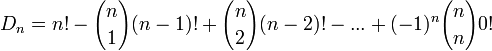 Это соотношение можно преобразовать к виду
Это соотношение можно преобразовать к виду
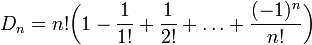 Нетрудно видеть, что выражение в скобках является частичной суммой ряда
Нетрудно видеть, что выражение в скобках является частичной суммой ряда 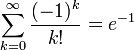 . Таким образом, с хорошей точностью число беспорядков составляет
. Таким образом, с хорошей точностью число беспорядков составляет 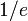 долю от общего числа
долю от общего числа 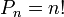 перестановок:
перестановок:
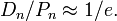 Число сюръективных отображений конечного
множества X; |X|= n, на конечное множество Y; |Y | = m, то
есть число функций f:XàY, таких, что f (X) = Y,
равно cогласно принципу включения-исключения:
f(n,m) =
Число сюръективных отображений конечного
множества X; |X|= n, на конечное множество Y; |Y | = m, то
есть число функций f:XàY, таких, что f (X) = Y,
равно cогласно принципу включения-исключения:
f(n,m) =  +
+ 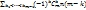 ^n =
^n = 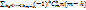 ^n
15.
Упорядоченные и неупорядоченные разбиения множеств. Число Стирлинга 2-го рода. Формула и рекуррентное соотношение для числа Стирлинга 2-го рода.
число Стирлинга второго рода
^n
15.
Упорядоченные и неупорядоченные разбиения множеств. Число Стирлинга 2-го рода. Формула и рекуррентное соотношение для числа Стирлинга 2-го рода.
число Стирлинга второго рода 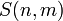 представляет собой количество неупорядоченных разбиений n -элементного множества на m частей, в то время какмультиномиальный коэффициент
представляет собой количество неупорядоченных разбиений n -элементного множества на m частей, в то время какмультиномиальный коэффициент 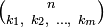 выражает количество упорядоченных разбиений n -элементного множества на m частей фиксированного размера
выражает количество упорядоченных разбиений n -элементного множества на m частей фиксированного размера 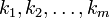 . Количество всех неупорядоченных разбиений n -элементного множества задается числом Белла
. Количество всех неупорядоченных разбиений n -элементного множества задается числом Белла 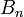 .
Числом Стирлинга второго рода из n по k, обозначаемым
.
Числом Стирлинга второго рода из n по k, обозначаемым 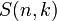 или
или 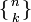 , называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
Числа Стирлинга второго рода удовлетворяют рекуррентному соотношению:
, называется количество неупорядоченных разбиений n -элементного множества на k непустых подмножеств.
Числа Стирлинга второго рода удовлетворяют рекуррентному соотношению:
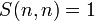 , для n ≥ 0,
, для n ≥ 0,
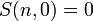 , для n > 0,
, для n > 0,
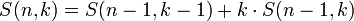 для
для 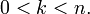
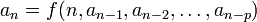 , выражающая каждый член последовательности
, выражающая каждый член последовательности 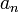 через p предыдущих членов. Например - числа Фибоначчи
через p предыдущих членов. Например - числа Фибоначчи 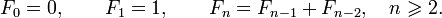 Линейным рекуррентным соотношением k - го порядка(k - фиксировано) с постоянными коэффициентами называется рекуррентное соотношение следующего вида:
Линейным рекуррентным соотношением k - го порядка(k - фиксировано) с постоянными коэффициентами называется рекуррентное соотношение следующего вида:
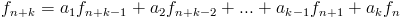 (3)
(3)
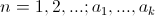 - постоянные
- постоянные 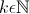 .
Характеристическим уравнением рекуррентного соотношения (3) является уравнение вида
.
Характеристическим уравнением рекуррентного соотношения (3) является уравнение вида
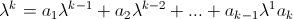 Теорема 2: Пусть
Теорема 2: Пусть  - все попарно различные корни характеристического уравнения рекурретного соотношения (3)
- все попарно различные корни характеристического уравнения рекурретного соотношения (3) 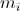 - кратность корня
- кратность корня 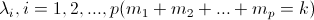 . Тогда общее решение рекуррентного соотношения (3) имеет следующий вид:
. Тогда общее решение рекуррентного соотношения (3) имеет следующий вид:
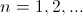 .
. 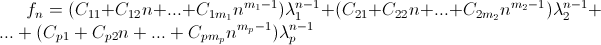 В частности, если
В частности, если 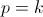 , то
, то
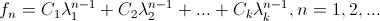 12
Общее решение линейного неоднородного рекуррентного соотношения с постоянными коэффициентами
Общее решение неоднородного рекурентного соотношения есть сумма общего решения однородного соотношения и какого-либо решения из неоднородных рекурентных соотношений.
Док-во
Пусть (
12
Общее решение линейного неоднородного рекуррентного соотношения с постоянными коэффициентами
Общее решение неоднородного рекурентного соотношения есть сумма общего решения однородного соотношения и какого-либо решения из неоднородных рекурентных соотношений.
Док-во
Пусть ( )-нек решение неоднордного соотнош, а (
)-нек решение неоднордного соотнош, а (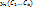 )-общее решоднороднсоотнош. Необход док-ть, что (
)-общее решоднороднсоотнош. Необход док-ть, что (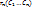 ) =
) = 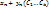 -общее решнеоднорднсоотнош.
-общее решнеоднорднсоотнош. 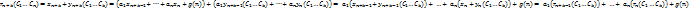 Мы доказали, что
Мы доказали, что  решения неоднород соотнош сущ-т
решения неоднород соотнош сущ-т 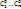 , что посл-сть (
, что посл-сть ( )уд неоднородсоотнош. Для этого запишем
)уд неоднородсоотнош. Для этого запишем 
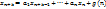 Вычитаем одно из 2ого и получаем:
Вычитаем одно из 2ого и получаем:
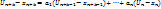 Т.о. получаем, что (
Т.о. получаем, что ( ) – общее реш однородного соотнош, т.к. сущ-т общее реш неоднород соотнош
) – общее реш однородного соотнош, т.к. сущ-т общее реш неоднород соотнош 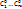 такое, что
такое, что 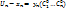 , т.е. вып-тся
, т.е. вып-тся 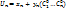 =>
=> 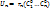
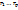 крастностей соответственно
крастностей соответственно 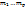 , тогда посл-сть (
, тогда посл-сть (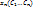 )явл общим решением, где
)явл общим решением, где 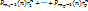 , где
, где 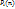 - мн-н степени не выше i, завис от n
Док-во
Поскольку
- мн-н степени не выше i, завис от n
Док-во
Поскольку  явл корнем характеристического ур-ния рекур соотнош, значит каждая посл-ть (
явл корнем характеристического ур-ния рекур соотнош, значит каждая посл-ть ( ) явл решение рекурсоотнош. Докажем теор для случая када кратность корней равна 1. Тогда рав-во можно переписать виде:
) явл решение рекурсоотнош. Докажем теор для случая када кратность корней равна 1. Тогда рав-во можно переписать виде: 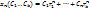 , p=k. Следвательнолин комбинация(
, p=k. Следвательнолин комбинация( – решение рекур соотнош
Необход д-ть, что эти решения будут общими,т.е. необход, чтобы
– решение рекур соотнош
Необход д-ть, что эти решения будут общими,т.е. необход, чтобы 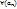 сущ-ли
сущ-ли 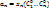 . Рассмотрим
при n=0:
. Рассмотрим
при n=0: 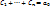 ,
при n=1:
,
при n=1: 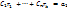 …
при n=k-1:
…
при n=k-1:  =
= 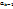 Получ система ур-ний из kур-ний с неизвестными
Получ система ур-ний из kур-ний с неизвестными  , относ кот нужно выяснить имеет ли реш данная система. Опр данной системы будет явл
, относ кот нужно выяснить имеет ли реш данная система. Опр данной системы будет явл
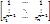 =
= 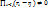 Т.о. мы получили, что ранг матрицы данной системы равен рангу рассмотр матрицы, значит даннай система совместима, а это означ, что сущ-т решение
Т.о. мы получили, что ранг матрицы данной системы равен рангу рассмотр матрицы, значит даннай система совместима, а это означ, что сущ-т решение  13
Разбиение подстановки на циклы. Число подстановок n -элементного множества, имеющих предписанных циклический тип.
Циклом длины lназ. такая подстановка а конечного множества Y={y1,..., у l ], что ш
13
Разбиение подстановки на циклы. Число подстановок n -элементного множества, имеющих предписанных циклический тип.
Циклом длины lназ. такая подстановка а конечного множества Y={y1,..., у l ], что ш
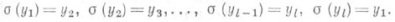 Конечный цикл обозначается (y1, y2,..., yl). Бесконечным циклом наз. такая П. счетного множества
Конечный цикл обозначается (y1, y2,..., yl). Бесконечным циклом наз. такая П. счетного множества
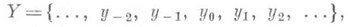 что для любого целого i s(yi)= yi+1 Обозначение бесконечного цикла таково:
что для любого целого i s(yi)= yi+1 Обозначение бесконечного цикла таково:
 Цикл длины 2 есть транспозиция. Группа Sn содержит (п- 1)! циклов длины п. Для любой подстановки g из S(X).существует такое разбиение множества X на непересекающиеся подмножества, что на каждом из них g действует как цикл. Конечные подмножества этого разбиения имеют вид
Цикл длины 2 есть транспозиция. Группа Sn содержит (п- 1)! циклов длины п. Для любой подстановки g из S(X).существует такое разбиение множества X на непересекающиеся подмножества, что на каждом из них g действует как цикл. Конечные подмножества этого разбиения имеют вид
 где g l (x}=x, а бесконечные -
где g l (x}=x, а бесконечные -
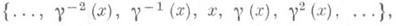
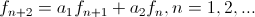 (2)
(2)
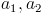 - нейкие коэффициенты, причем
- нейкие коэффициенты, причем 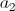 отлично от нуля. Уравнение вида
отлично от нуля. Уравнение вида
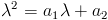 - характеристическое уравнение рекуррентного соотношения (2).
Теорема 1: Если характеристическое уравнение рекуррентного соотношения (2) имеет два различных корня
- характеристическое уравнение рекуррентного соотношения (2).
Теорема 1: Если характеристическое уравнение рекуррентного соотношения (2) имеет два различных корня 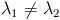 , то общее решение рекуррентного соотношения (2) имеет вид
, то общее решение рекуррентного соотношения (2) имеет вид
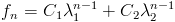 Если рекуррентное соотношение имеет два равных корня
Если рекуррентное соотношение имеет два равных корня 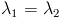 , то общее решение рекуррентного соотношения (2) имеет следующий вид
, то общее решение рекуррентного соотношения (2) имеет следующий вид
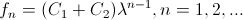 последовательность чисел Фибоначчи
последовательность чисел Фибоначчи 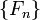 задается линейным рекуррентным соотношением:
задается линейным рекуррентным соотношением: 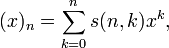 где
где 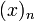 — символ Похгаммера (убывающий факториал):
— символ Похгаммера (убывающий факториал):
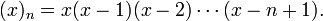 Как видно из определения, числа имеют чередующийся знак. Их абсолютные значения задают количество перестановок множества, состоящего из n элементов с k циклами.
Числа Стирлинга первого рода задаются рекуррентным соотношением:
Как видно из определения, числа имеют чередующийся знак. Их абсолютные значения задают количество перестановок множества, состоящего из n элементов с k циклами.
Числа Стирлинга первого рода задаются рекуррентным соотношением:
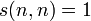 , для n ≥ 0,
, для n ≥ 0,
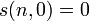 , для n > 0,
, для n > 0,
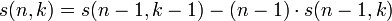 для
для  ={0;1},
={0;1},  -двоичное представление числа k,
-двоичное представление числа k, 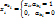 7
Теор о ед-сти представ бул ф-циипоср-ом п.Жегалкина
Для любой булевой ф-циисущ-т в точности один полином Жегалкина.
Док-во
f=f(
7
Теор о ед-сти представ бул ф-циипоср-ом п.Жегалкина
Для любой булевой ф-циисущ-т в точности один полином Жегалкина.
Док-во
f=f(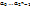 ). Каждый полином Жегалкина однозначно определяется вектором (
). Каждый полином Жегалкина однозначно определяется вектором (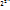 , а это число всех булевых функций от n переменных, т.е каждой функции соответствует свой полином Жегалкина
, а это число всех булевых функций от n переменных, т.е каждой функции соответствует свой полином Жегалкина
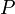 функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим:
функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: 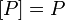 . Другими словами, любая функция, которую можно выразить формулой с использованием функций множества
. Другими словами, любая функция, которую можно выразить формулой с использованием функций множества  - сохрconst 0 – явлзамкнутым
Док-во
Пусть ф-цииg=g(
- сохрconst 0 – явлзамкнутым
Док-во
Пусть ф-цииg=g(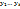 ) и
) и  =f(
=f(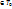 . Пусть h-суперпозиция. Рассмотрим h=h(0, … 0) = g(
. Пусть h-суперпозиция. Рассмотрим h=h(0, … 0) = g(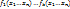 ) = g(0, … 0) = 0
2. Класс
) = g(0, … 0) = 0
2. Класс  - сохрconst 1 – явлзамкнутым
Док-воаналогичное
3. Класс
- сохрconst 1 – явлзамкнутым
Док-воаналогичное
3. Класс  –самодвойственная ф-ция – явл замкнутым
Док-во
Пусть ф-цииg=g(
–самодвойственная ф-ция – явл замкнутым
Док-во
Пусть ф-цииg=g( ) = g(
) = g(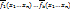 ) =
) =  (
( (
( –монотонная ф-ция – явл замкнутым
Док-во
–монотонная ф-ция – явл замкнутым
Док-во
 )и
)и  = (
= ( )
) 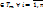 . Пусть h-суперпозиция. Скажем, что
. Пусть h-суперпозиция. Скажем, что 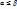 . h(
. h(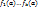 )
)  g(
g(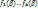 ) = h(
) = h( –линейная ф-ция – явл замкнутым
Док-во
Т.к. суперпозиция полинома Жегалкина степени не выше 1 так же явл полиномом степени не выше 1.
–линейная ф-ция – явл замкнутым
Док-во
Т.к. суперпозиция полинома Жегалкина степени не выше 1 так же явл полиномом степени не выше 1.
 функций алгебры логики называется полной системой, если замыкание этого множества совпадает с множеством всех функций. (В частности, для двузначной логики
функций алгебры логики называется полной системой, если замыкание этого множества совпадает с множеством всех функций. (В частности, для двузначной логики 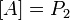 .) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества
.) Другими словами, должна быть возможность любую функцию алгебры логики выразить формулой с использованием функций множества 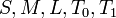 , т.е. когда в ней имеется хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция
, т.е. когда в ней имеется хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция
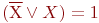 .
Пусть
.
Пусть 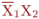 – простая импликанта некоторой
– простая импликанта некоторой 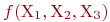 трех переменных. Тогда:
трех переменных. Тогда:
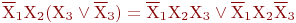 получатся после многократного применения этой операции дизъюнкции конституент единицы исходной функции, т.е. ее СДНФ.
получатся после многократного применения этой операции дизъюнкции конституент единицы исходной функции, т.е. ее СДНФ.
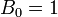 .
Числа Белла можно задать в рекуррентном виде:
.
Числа Белла можно задать в рекуррентном виде:
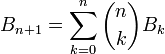 .
Число Белла можно вычислить как сумму чисел Стирлинга второго рода:
.
Число Белла можно вычислить как сумму чисел Стирлинга второго рода:
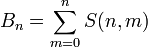 20
Теорема Рамсея.
Пусть
20
Теорема Рамсея.
Пусть  и
и  — натуральные числа, причем
— натуральные числа, причем 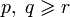 . Тогда существует число
. Тогда существует число 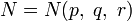 , обладающее следующим свойством: если все
, обладающее следующим свойством: если все  -элементного множества
-элементного множества 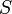 произвольным образом разбиты на два непересекающихся семейства
произвольным образом разбиты на два непересекающихся семейства 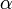 и
и 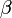 , то либо существует
, то либо существует 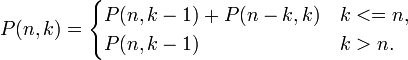 Количество разбиений натурального числа n на k слагаемых:
Количество разбиений натурального числа n на k слагаемых: 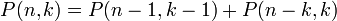 21
Булевы функции. Способы их задания. Число бул. Ф-ий от n переменных.
Логической (булевой) функцией (или просто функцией) n переменных y = f(x 1, x 2, …, xn) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.
Кол-во бул.ф-ий 2^(2^ n)
1. Табличный
21
Булевы функции. Способы их задания. Число бул. Ф-ий от n переменных.
Логической (булевой) функцией (или просто функцией) n переменных y = f(x 1, x 2, …, xn) называется такая функция, у которой все переменные и сама функция могут принимать только два значения: 0 и 1.
Кол-во бул.ф-ий 2^(2^ n)
1. Табличный

 ). Тогда для Т сущ-т система различных представителей такая, что
). Тогда для Т сущ-т система различных представителей такая, что  и
и  подмн-ва {
подмн-ва {  }
}  [m] вып-тся условие: |
[m] вып-тся условие: |  |
|  k
k сод-т kэл-товмн-ва С. Учитывая вкл
сод-т kэл-товмн-ва С. Учитывая вкл  эл-тов долно быть больше, чем k?!
эл-тов долно быть больше, чем k?!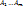 }. Рассмотрим набор Тподмн-вамн-ваS’. T=(
}. Рассмотрим набор Тподмн-вамн-ваS’. T=( ={
={ 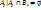 }. Если взять i=1, то получается, что
}. Если взять i=1, то получается, что 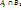 … при i=m:
… при i=m: 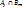 . РокажемЮч то для Т сущ-т система различных представителей (теор Холла)
. РокажемЮч то для Т сущ-т система различных представителей (теор Холла) 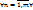 подмн-ва {
подмн-ва {  |
|  }?! Покажем, что мн-во
}?! Покажем, что мн-во 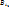 c
c  а
а 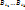 , значит для набора Т сущ-т система различных представителей. Выберем в
, значит для набора Т сущ-т система различных представителей. Выберем в 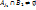 c
c  аналогично и для
аналогично и для  c
c  . Получим С={
. Получим С={ 

