Переменного»
5) Найти  ,
,  ,
, 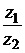 , если
, если  ,
, 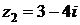 .
.
Решение.
 ;
;
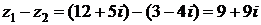 ;
;
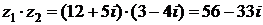 ;
;


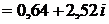 .
.
6) Решить уравнение 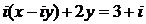 .
.
Решение.
Раскроем скобки:  .
.
Создадим систему: 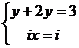 .
.
Следовательно,  Получаем:
Получаем: 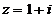
7) Найти все значения 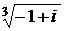 .
.
Решение.
Запишем в тригонометрической форме: 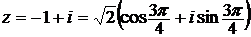 .
.
Теперь используем формулу Муавра
 ,
, 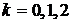 .
.
Отсюда получаем три значения корня:
8) Изобразить область, ограниченную линиями:
а) 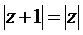
 Решение.
Решение.
Преобразуем: 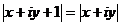
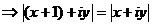
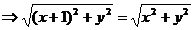
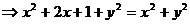
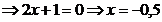
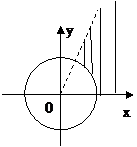 б)
б) 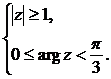
9) Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй – 0,8, третий – 0,7. Пусть события 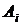 – студент сдаст i -ый экзамен
– студент сдаст i -ый экзамен 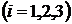 .
.
Написать формулу, выражающую следующие события через события  и вычислить вероятность этих событий:
и вычислить вероятность этих событий:
а) событие В - студент будет сдан только 2–ой экзамен;
б) событие С - студентом будет сдан только один экзамен;
в) событие D - студентом будут сданы три экзамена;
г) событие E - студентом будет сдано два экзамена;
д) событие F - студентом будет сдан хотя бы один экзамен.
Решение.
Т.к. события 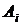 – студент сдаст i -ый экзамен
– студент сдаст i -ый экзамен 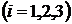 , тогда вероятности
, тогда вероятности
| i
| сдачи экзаменов
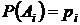
| не сдачи экзаменов

|
| 1
| 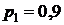
| 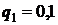
|
| 2
| 
| 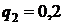
|
| 3
| 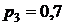
| 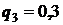
|
а) Событие В – студент сдаст только 2-ой экзамен состоит в том, что студент сдаст 2-ой экзамен и не сдаст 1-ый и 3-ий экзамены, т.е. 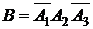 , учитывая что события независимы, получим
, учитывая что события независимы, получим
 .
.
б) Событие С – студент сдаст один экзамен из трех, т.е. сдаст или 1-й экзамен из трех, или 2-й, или 3-й из трех экзаменов. Следовательно, событие  .
.
Т.к. события 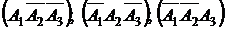 несовместны, то
несовместны, то
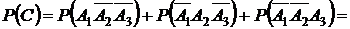
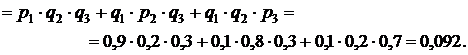
в) Событие D – студент сдаст все три экзамена, т.е. 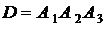 . Тогда
. Тогда
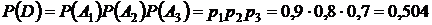 .
.
г) Событие Е – студент сдаст два экзамен из трех, т.е. не сдаст или 1-й экзамен из трех, или 2-й, или 3-й из трех экзаменов.
Следовательно, событие 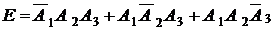 . Т. к. события
. Т. к. события  несовместны, то
несовместны, то
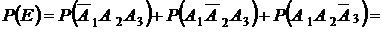
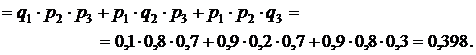
д) Пусть событие F – студент сдаст хотя бы один экзамен. Удобнее записать это событие, если перейти к противоположному событию:  .
.
Противоположное событие 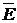 заключается в том, что студент не сдаст ни один экзамен, т.е. и 1-й не сдаст, и 2-й не сдаст, и 3-й не сдаст.
заключается в том, что студент не сдаст ни один экзамен, т.е. и 1-й не сдаст, и 2-й не сдаст, и 3-й не сдаст.
Значит, событие 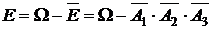 и вероятность данного события равна
и вероятность данного события равна
 .
.
Ответ: а) 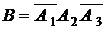 ,
, 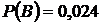 ;
;
б)  ,
, 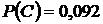 ;
;
в) 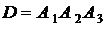 ,
, 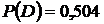 ;
;
г)  ,
, 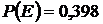 ;
;
д) 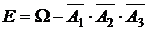 ,
, 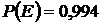 .
.
10) При включении зажигания двигатель начнет работать с вероятностью 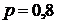 . Пусть событие
. Пусть событие 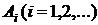 двигатель начнет работать при i -ом включении зажигания. Событие В состоит в том, что двигатель начнет работать при третьем включении зажигания; С – для запуска двигателя придется включать зажигание не более трех раз.
двигатель начнет работать при i -ом включении зажигания. Событие В состоит в том, что двигатель начнет работать при третьем включении зажигания; С – для запуска двигателя придется включать зажигание не более трех раз.
Написать формулу выражающую события В и С через события 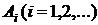 и вычислить вероятность этих событий.
и вычислить вероятность этих событий.
Решение.
Т. к. событие 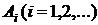 – двигатель начнет работать при i-ом включении зажигания, то
– двигатель начнет работать при i-ом включении зажигания, то 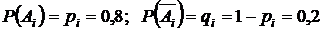 .
.
Тогда событие В – двигатель начнет работать при третьим зажигании, следовательно, при 1-ом и при 2-ом зажигание не сработало. Событие В можно представить в виде 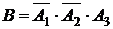 и вероятность этого события равна
и вероятность этого события равна
 .
.
Событие С – для запуска придется включать зажигание не более трех раз. Событие С – наступит, если двигатель начнет работать при 1-м, или при 2-м, или при 3-м включении, т.е. 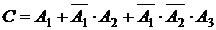 и, следовательно, вероятность события С
и, следовательно, вероятность события С
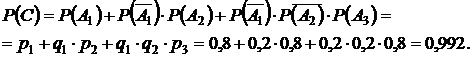
Ответ: 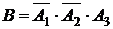 ,
, 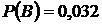 ;
;
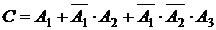 ,
, 
11) Пусть вероятность того, что студент опоздает на лекцию, равна 0,08. Найти вероятность того, что среди 96 студентов на лекцию опоздает не более 3-х человек 1) по биномиальной формуле, 2) по формуле Пуассона.
Решение.
Решение задачи основывается на вычислении вероятностей 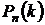 .
.
Событие А – «на лекцию опоздает не более 3-х человек» означает, что опоздает или 0, или 1, или 2, или 3 студента, т. е. k = 0, или k = 1, или k = 2, или k = 3.
Искомая вероятность определяется:
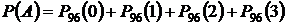 .
.
Вычислим 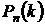 разными способами.
разными способами.
1) по биномиальной формуле (формуле Бернулли): 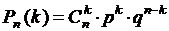 ,
,
где 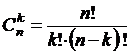 ,
, 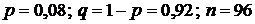 .
.

2) Т. к. 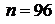 ,
,  и
и 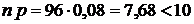 , то искомую вероятность можно вычислить по приближенной формуле Пуассона
, то искомую вероятность можно вычислить по приближенной формуле Пуассона
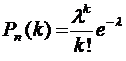 , где
, где 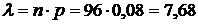 .
.
Вычисляем вероятность по формуле Пуассона

Таким образом, получаем
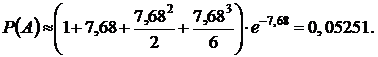
Ответ: а) 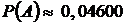 , б)
, б) 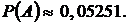
|
| 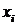
| 1
| 2
| 3
|
12) СВ 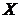 задана законом распределения. задана законом распределения.
| 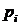
| 
| ?
| 
|
Найти:
1) числовые характеристики 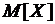 ,
, 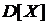 ;
;
2) функцию распределения 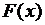 и построить ее график;
и построить ее график;
3) вероятность 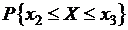 ;
;
4) закон распределения величины СВ  . Вычислить
. Вычислить  ,
, 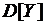 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно по составленному закону распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно по составленному закону распределения.
Решение.
В задаче рассматривается дискретная СВ Х, заданная рядом распределения. По свойству ряда 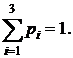 Отсюда получаем
Отсюда получаем 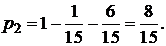
1) Математическое ожидание:
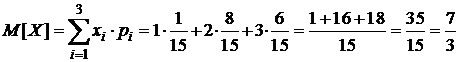 .
.
Дисперсия:
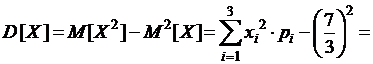
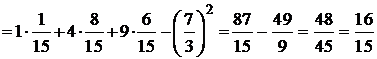 .
.
Среднее квадратическое отклонение: 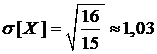 .
.
| 2) Функция распределения имеет вид (рис. 1):
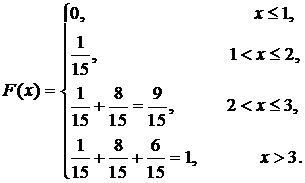
| 
|
| Рис. 1
|
3) 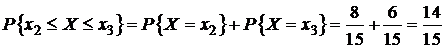 .
.
4) 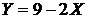 – дискретная СВ. Составим для нее ряд распределения:
– дискретная СВ. Составим для нее ряд распределения:
Вычислим числовые характеристики СВ 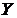 , используя составленный ряд:
, используя составленный ряд:
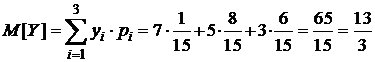 .
.
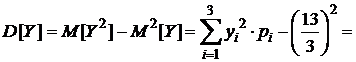
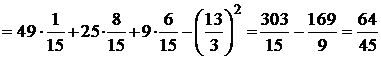 .
.
Вычислим числовые характеристики СВ 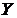 , используя их свойства:
, используя их свойства:
 .
.
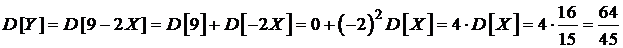 .
.
Ответ: 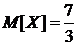 ,
, 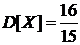 ,
, 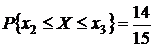 ,
, 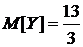 ,
,  .
.
14) Плотность вероятности непрерывной СВ X задана функцией

 Найти:
Найти:
| 1)
| параметр С и построить график 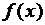 ; ;
|
| 2)
| интегральную функцию 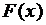 и построить ее график; и построить ее график;
|
| 3)
| математическое ожидание 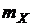 , дисперсию , дисперсию 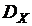 и среднее квадратическое отклонение и среднее квадратическое отклонение 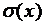 ; ;
|
| 4)
| вероятность 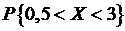 дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках. дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
|
Решение.
Данный закон распределения является непрерывным.
1) По свойству плотности (дифференциальной функции):

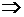
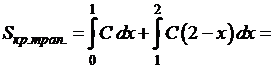
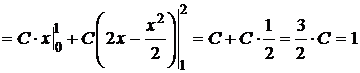
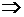
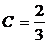 .
.
Получаем функцию:
| 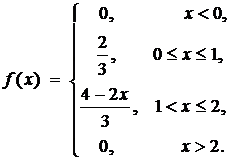
|
и ее график (рис. 3).
| 
|
| Рис. 3
|
2) Найдём интегральную функцию, учитывая свойства:
· если  , то
, то 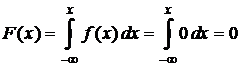 ;
;
· если 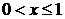 , то
, то
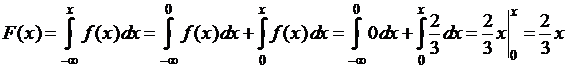 ;
;
· если 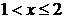 , то
, то
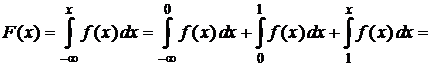
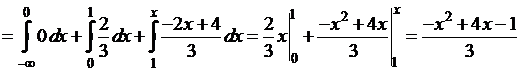 .
.
· если 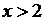 , то
, то

 .
.
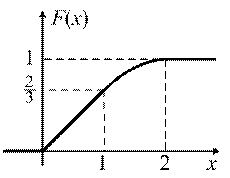
| В итоге получаем функцию и её график (рис. 4)

| 
|
| Рис. 4
|
3) Вычислим числовые характеристики:
· математическое ожидание:

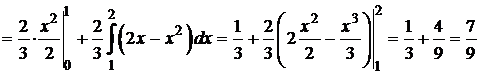 ;
;
· дисперсию по формуле 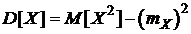 :
:
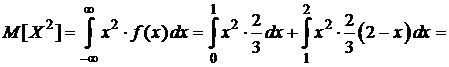
 ;
;
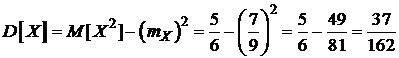 ;
;
· среднее квадратическое отклонение: 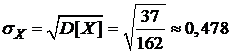 .
.
4) Найдём вероятность того, что СВ X примет значения из интервала 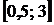 двумя способами:
двумя способами:
| q 
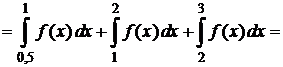
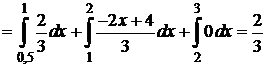 . .
Здесь вероятность численно равна площади выделенной фигуры (рис. 5).
q 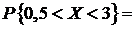
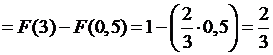 . .
В этом случае вероятность численно равна длине отрезка на оси 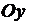 (рис. 6). (рис. 6).
При этом результаты вычислений совпадают при различных способах.
| 
|
| Рис. 5
|

|
| Рис. 6
|
Ответ: 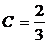 ;
; 
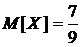 ;
; 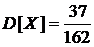 ;
;  ;
; 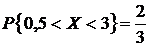 .
.
15) В результате опыта получена выборочная совокупность:
| 88
| 104
| 91
| 97
| 77
| 103
| 86
| 79
| 86
| 100
| 84
| 74
| 76
| 75
| 93
| 103
| 80
| 96
| 72
| 95
|
| 82
| 68
| 71
| 87
| 89
| 89
| 81
| 81
| 70
| 79
| 81
| 102
| 75
| 80
| 90
| 85
| 82
| 77
| 94
| 102
|
| 84
| 91
| 87
| 83
| 90
| 69
| 83
| 96
| 79
| 94
| 87
| 95
| 99
| 83
| 80
| 93
| 90
| 79
| 93
| 105
|
| 93
| 86
| 81
| 83
| 84
| 92
| 93
| 85
| 84
| 88
| 95
| 85
| 84
| 90
| 93
| 95
| 98
| 88
| 79
| 91
|
| 77
| 85
| 93
| 85
| 87
| 100
| 76
| 79
| 90
| 91
| 86
| 88
| 93
| 80
| 88
| 88
| 90
| 68
| 89
| 90
|
1. По данной таблице составить интервальный вариационный ряд, разбив всю вариацию на 8-10 интервалов.
2. По сгруппированным данным построить:
| а)
| полигон относительных частот;
|
| б)
| гистограмму относительных частот;
|
| в)
| график эмпирической функции распределения.
|
3. Найти числовые характеристики выборочной совокупности:  ,
, 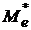 ,
,  ,
, 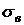 , s.
, s.
4. Построить:
| а)
| на чертеже гистограммы её теоретический аналог 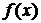 ; ;
|
| б)
| на чертеже эмпирической функции  её теоретический аналог её теоретический аналог  . .
|
5. По виду гистограммы и эмпирической функции распределения выборки выдвинуть гипотезу о распределении генеральной совокупности.
6. Проверить выполнение правила «трёх сигм».
7. Применив критерий согласия Пирсона  с заданным уровнем значимости
с заданным уровнем значимости 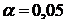 , окончательно принять или отвергнуть выдвинутую гипотезу о распределении генеральной совокупности.
, окончательно принять или отвергнуть выдвинутую гипотезу о распределении генеральной совокупности.
8. Построить на одном чертеже:
| а)
| полигон относительных частот  и кривую распределения и кривую распределения 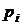 . Сравнить график . Сравнить график 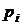 с графиком идеально нормального распределения; с графиком идеально нормального распределения;
|
| б)
| гистограмму теоретических вероятностей (относительных частот) 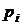 и график и график 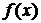 . .
|
9. Найти доверительные интервалы для генеральной средней и генерального среднего квадратического отклонения по уровню надёжности  .
.
Решение.
1. Разобьем всю вариацию объёмом 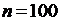 на
на 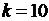 частичных интервалов равной длины и посчитаем частоты попадания наблюдаемых значений в частичные интервалы.
частичных интервалов равной длины и посчитаем частоты попадания наблюдаемых значений в частичные интервалы.
Длину интервала находим по формуле 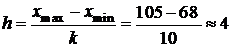 .
.
За начало первого интервала примем 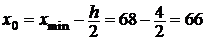 . Получим последовательность интервалов: [66; 70], (70; 74], …, (102; 106].
. Получим последовательность интервалов: [66; 70], (70; 74], …, (102; 106].
Составим вариационный ряд частот и относительных частот:

| интервал
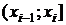
| середина
интервала

| частота
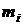
| относительная частота
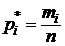
|
| 1
| [66; 70]
| 68
| 4
| 0,04
|
| 2
| (70; 74]
| 72
| 3
| 0,03
|
| 3
| (74; 78]
| 76
| 7
| 0,07
|
| 4
| (78; 82]
| 80
| 16
| 0,16
|
| 5
| (82; 86]
| 84
| 18
| 0,18
|
| 6
| (86; 90]
| 88
| 20
| 0,20
|
| 7
| (90; 94]
| 92
| 15
| 0,15
|
| 8
| (94; 98]
| 96
| 7
| 0,07
|
| 9
| (98; 102]
| 100
| 6
| 0,06
|
| 10
| (102; 106]
| 104
| 4
| 0,04
|
| Σ
| –
| –
| 100
| 1
|
Отметим, что 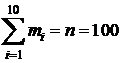 – объём выборки;
– объём выборки; 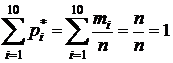 .
.
Статистическое распределение выборки является оценкой неизвестного распределения. В частности, относительные частоты  являются статистическими аналогами вероятностей полной группы несовместных событий.
являются статистическими аналогами вероятностей полной группы несовместных событий.
2. Вторым этапом обработки статистических данных является построение полигона, гистограммы относительных частот и эмпирической функции распределения.
а) Полигон относительных частот вариационного ряда – ломаная линия, соединяющая точки 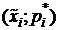 .
График полигона представлен на рис. 11. .
График полигона представлен на рис. 11.
| 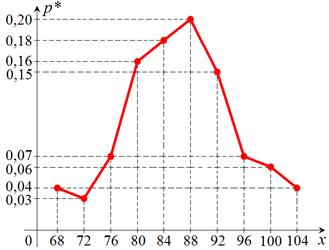 Рис. 11
Рис. 11
|
Полигон относительных частот является статистическим аналогом многоугольника распределения дискретной случайной величины Х.
б) Гистограмма относительных частот изображается только для интервального ряда и имеет вид ступенчатой фигуры (рис. 12).
На каждом частичном интервале строим прямоугольник высотой  . .
| 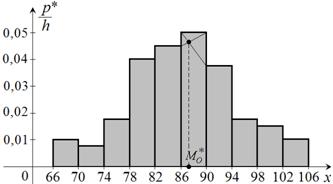 Рис. 12
Рис. 12
|
Гистограмма относительных частот является статистическим аналогом дифференциальной функции распределения (плотности) 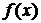 непрерывной случайной величины Х.
непрерывной случайной величины Х.
в) График эмпирической функции распределения  непрерывной случайной величины X совпадает с кумулятой (графиком накопленных частот).
непрерывной случайной величины X совпадает с кумулятой (графиком накопленных частот).
Отметим на плоскости точки, соответствующие значениям функции  на концах интервалов, и соединим их отрезками прямых (рис. 13).
на концах интервалов, и соединим их отрезками прямых (рис. 13).
| 
| 70
| 74
| 78
| 82
| 86
| 90
| 94
| 98
| 102
| 
|
| 0
| 0,04
| 0,07
| 0,14
| 0,30
| 0,48
| 0,68
| 0,83
| 0,90
| 0,96
| 1
|
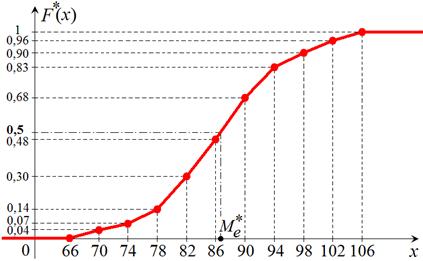
Рис. 13
Эмпирическая функция распределения  является статистическим аналогом интегральной функции распределения
является статистическим аналогом интегральной функции распределения  случайной величины Х.
случайной величины Х.
3. Найдем числовые характеристики выборки.
Выборочные характеристики – это функции наблюдений, приближённо оценивающие соответствующие числовые характеристики случайной величины.
1) Мода 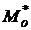 находится внутри интервала, для которого соответствующая частота максимальна. В нашем случае
находится внутри интервала, для которого соответствующая частота максимальна. В нашем случае 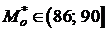 , при этом
, при этом 
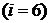 .
.
Моду можно определить на чертеже гистограммы (рис. 12) или вычислить по формуле
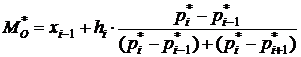 ,
,
где 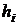 – длина частичного интервала
– длина частичного интервала  ,
,
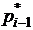 – частость, соответствующая предыдущему частичному интервалу
– частость, соответствующая предыдущему частичному интервалу 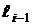 ,
,
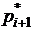 – частость, соответствующая следующему частичному интервалу
– частость, соответствующая следующему частичному интервалу 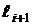 .
.
Тогда получим
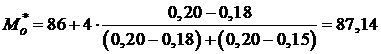 .
.
2) Медиана 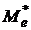 интервального вариационного ряда принадлежит тому частотному интервалу, для которого накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины всей суммы частот. Геометрически прямая
интервального вариационного ряда принадлежит тому частотному интервалу, для которого накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины всей суммы частот. Геометрически прямая  делит площадь гистограммы пополам.
делит площадь гистограммы пополам.
Медиана может быть приближённо найдена на чертеже графика  (рис. 13), как значение признака, для которого
(рис. 13), как значение признака, для которого 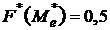 . Для данного вариационного ряда значение
. Для данного вариационного ряда значение 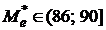 .
.
Значение 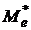 вычисляем по формуле
вычисляем по формуле
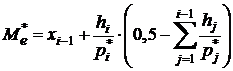 .
.
Тогда получим
 .
.
3) Для нахождения выборочной средней 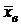 , выборочной дисперсии
, выборочной дисперсии 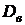 , выборочного среднего квадратического отклонения
, выборочного среднего квадратического отклонения 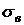 (статистические аналоги соответствующих числовых характеристик случайной величины) заполним вспомогательную таблицу.
(статистические аналоги соответствующих числовых характеристик случайной величины) заполним вспомогательную таблицу.
| i
| 
| 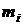
| 
| 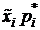
| 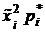
|
| 1
| 68
| 4
| 0,04
| 2,72
| 184,96
|
| 2
| 72
| 3
| 0,03
| 2,16
| 155,52
|
| 3
| 76
| 7
| 0,07
| 5,32
| 404,32
|
| 4
| 80
| 16
| 0,16
| 12,80
| 1024,00
|
| 5
| 84
| 18
| 0,18
| 15,12
| 1270,08
|
| 6
| 88
| 20
| 0,2
| 17,60
| 1548,80
|
| 7
| 92
| 15
| 0,15
| 13,80
| 1269,60
|
| 8
| 96
| 7
| 0,07
| 6,72
| 645,12
|
| 9
| 100
| 6
| 0,06
| 6,00
| 600,00
|
| 10
| 104
| 4
| 0,04
| 4,16
| 432,64
|
| Σ
| –
| 100
| 1
| 86,4
| 7535,04
|
Находим выборочное среднее:
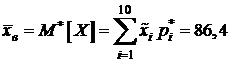 ;
;
выборочную дисперсию:
 ;
;
выборочное среднее квадратическое отклонение: 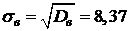 ;
;
исправленную выборочную дисперсию:
 ;
;
исправленное выборочное среднее квадратическое отклонение
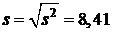 .
.
Т. к. число наблюдений 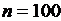 достаточно велико, то вместо
достаточно велико, то вместо 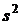 можно использовать неисправленную выборочную дисперсию
можно использовать неисправленную выборочную дисперсию  .
.
4. Точечной оценкой математического ожидания 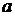 является средняя выборочная
является средняя выборочная 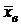 , тогда полагаем
, тогда полагаем  ; точечной оценкой генерального среднего квадратического отклонения
; точечной оценкой генерального среднего квадратического отклонения  является исправленное выборочное среднее квадратическое отклонение, т. е.
является исправленное выборочное среднее квадратическое отклонение, т. е. 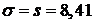 .
.
а) Вид гистограммы относительных частот напоминает график плотности функции 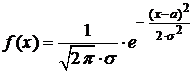 нормального распределения непрерывной случайной величины
нормального распределения непрерывной случайной величины 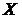 .
.
Построим на одном чертеже с гистограммой относительных частот  (рис. 11) её теоретический аналог
(рис. 11) её теоретический аналог  (рис. 14).
(рис. 14).

Рис. 14
б) Вид эмпирической функции распределения  напоминает интегральную функцию
напоминает интегральную функцию 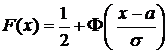 нормального распределения. Построим на одном чертеже с эмпирической функцией
нормального распределения. Построим на одном чертеже с эмпирической функцией  (рис. 12) её теоретический аналог
(рис. 12) её теоретический аналог 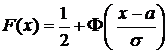 , где
, где  ,
, 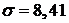 (рис. 15).
(рис. 15).

|
| Рис. 15
|
5. По виду гистограммы и функции  выдвигаем основную (нулевую) гипотезу
выдвигаем основную (нулевую) гипотезу 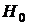 : «Генеральная совокупность распределена по нормальному закону с параметрами
: «Генеральная совокупность распределена по нормальному закону с параметрами  ,
, 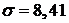 » и альтернативную гипотезу
» и альтернативную гипотезу  : «Генеральная совокупность не распределена по нормальному закону».
: «Генеральная совокупность не распределена по нормальному закону».
6. Проверим выполнение правила «трёх сигм»:
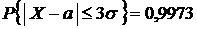 ,
,
которое требует, чтобы в 99,73 % значения случайной величины, распределенной по нормальному закону, попадали на отрезок 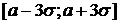 .
.
В нашем случае: 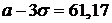 ,
, 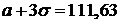 , отсюда получаем, что интервал опытных данных
, отсюда получаем, что интервал опытных данных 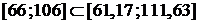 . Таким образом, найденный промежуток полностью накрыл наши статистические значения.
. Таким образом, найденный промежуток полностью накрыл наши статистические значения.
Т. к. условие правила «трёх сигм» выполняется, то есть основание предполагать, что изучаемое распределение является нормальным.
7. Проверим соответствие гипотезы 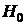 опытным данным.
опытным данным.
Для этого необходимо вычислить теоретические вероятности  и выравнивающие частоты
и выравнивающие частоты  .
.
Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений (т. е.  ). Т. к. число наблюдений в крайних интервалах меньше 5, то объединим их с соседними. Получим следующий ряд распределения:
). Т. к. число наблюдений в крайних интервалах меньше 5, то объединим их с соседними. Получим следующий ряд распределения:
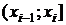
| [64; 74]
| (74; 78]
| (78; 82]
| (82; 86]
| (86; 90]
| (90; 94]
| (94; 98]
| (98; 106]
|
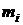
| 7
| 7
| 16
| 18
| 20
| 15
| 7
| 10
|
Найдём интервальные вероятности  . Т. к. случайная величина определена на интервале
. Т. к. случайная величина определена на интервале  , то крайние промежутки в ряде распределения заменяем, соответственно на
, то крайние промежутки в ряде распределения заменяем, соответственно на  и
и 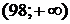 (рис. 16).
(рис. 16).
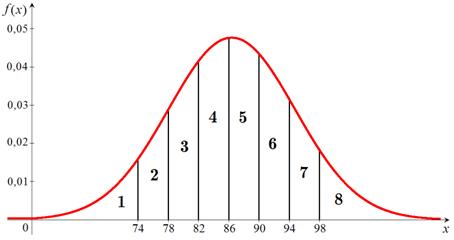
Рис. 16
Искомые вероятности вычисляем по формуле
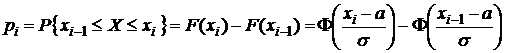 .
.
Используя таблицу приложения 2 и свойства функции Лапласа, находим:

 ;
;
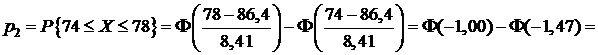
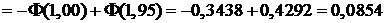 ;
;

 ;
;
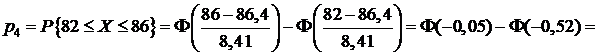
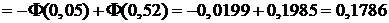 ;
;
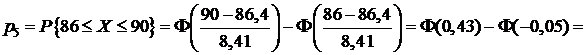
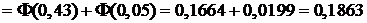 ;
;
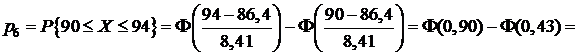
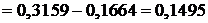 ;
;
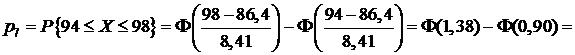
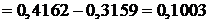 ;
;
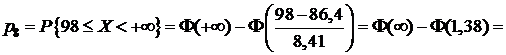
 .
.
Для дальнейших расчётов заполним вспомогательную таблицу:

| интервал
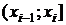
| частота
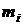
| теоретическая частота
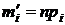
| 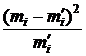
|
| 1
| (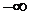 ; 74] ; 74]
| 7
| 7,08
| 0,0009
|
| 2
| (74; 78]
| 7
| 8,54
| 0,2777
|
| 3
| (78; 82]
| 16
| 14,53
| 0,1487
|
| 4
| (82; 86]
| 18
| 17,86
| 0,0011
|
| 5
| (86; 90]
| 20
| 18,63
| 0,1007
|
| 6
| (90; 94]
| 15
| 14,95
| 0,0002
|
| 7
| (94; 98]
| 7
| 10,03
| 0,9153
|
| 8
| (98; 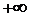 ) )
| 10
| 8,38
| 0,3132
|
| Σ
| –
| 100
| 100
| 1,7578
|
Наблюдаемое значение критерия согласия Пирсона (итоговая строка таблицы) 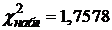 .
.
По таблице приложения 3 критических точек распределения  , по заданному уровню значимости
, по заданному уровню значимости 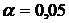 и числу степеней свободы
и числу степеней свободы 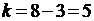 найдём критическое значение
найдём критическое значение  .
.
Т. к.  , то нет оснований отвергнуть проверяемую нулевую гипотезу. Т. е. принимаем предположение, что статистические данные распределены по нормальному закону с параметрами
, то нет оснований отвергнуть проверяемую нулевую гипотезу. Т. е. принимаем предположение, что статистические данные распределены по нормальному закону с параметрами  и
и 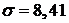 .
.
Полигон относительных частот  представляет данные, взятые по выборке. Кривая
представляет данные, взятые по выборке. Кривая 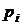 выравнивает эмпирические данные, тем самым приближая распределение генеральной совокупности к нормальному.
выравнивает эмпирические данные, тем самым приближая распределение генеральной совокупности к нормальному.
б) Построим на одном чертеже гистограмму теоретических вероятностей (относительных частот) 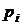 и график функции
и график функции 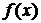 (рис. 18).
(рис. 18).
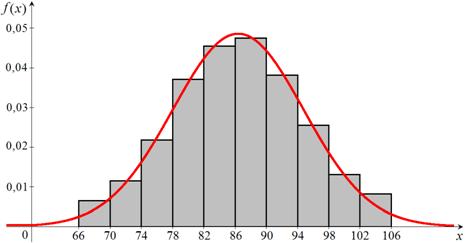
Рис. 18
9. Т. к. 
|
|
|



 ,
,  ,
, 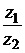 , если
, если  ,
, 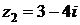 .
. ;
;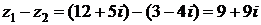 ;
;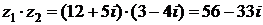 ;
;

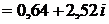 .
.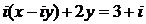 .
. .
.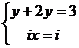 .
. Получаем:
Получаем: 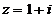
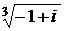 .
.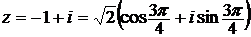 .
. ,
, 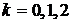 .
. ,
,  ,
,  ;
;
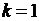 ,
, 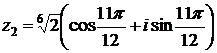 ,
, 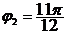 ;
;
 ,
, 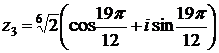 ,
,  .
.
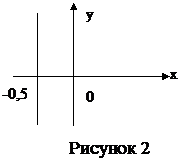
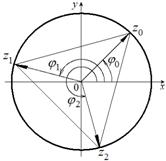
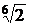 (рис. 2). Как видно из рисунка,
(рис. 2). Как видно из рисунка, 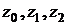 являются вершинами правильного треугольника.
являются вершинами правильного треугольника.
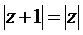
 Решение.
Решение.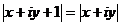
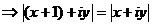
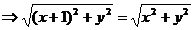
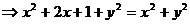
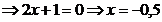
 б)
б) 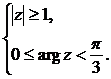
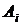 – студент сдаст i -ый экзамен
– студент сдаст i -ый экзамен 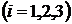 .
. и вычислить вероятность этих событий:
и вычислить вероятность этих событий: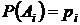

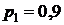
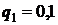

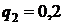
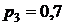
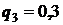
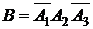 , учитывая что события независимы, получим
, учитывая что события независимы, получим .
. .
.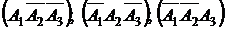 несовместны, то
несовместны, то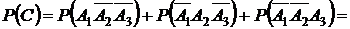
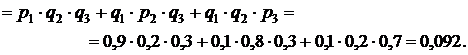
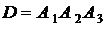 . Тогда
. Тогда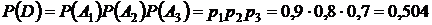 .
.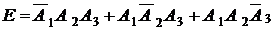 . Т. к. события
. Т. к. события  несовместны, то
несовместны, то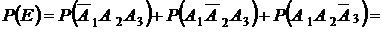
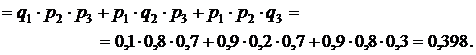
 .
.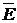 заключается в том, что студент не сдаст ни один экзамен, т.е. и 1-й не сдаст, и 2-й не сдаст, и 3-й не сдаст.
заключается в том, что студент не сдаст ни один экзамен, т.е. и 1-й не сдаст, и 2-й не сдаст, и 3-й не сдаст.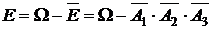 и вероятность данного события равна
и вероятность данного события равна .
.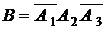 ,
, 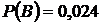 ;
; ,
, 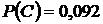 ;
;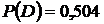 ;
; ,
, 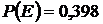 ;
;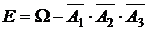 ,
, 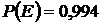 .
.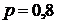 . Пусть событие
. Пусть событие 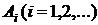 двигатель начнет работать при i -ом включении зажигания. Событие В состоит в том, что двигатель начнет работать при третьем включении зажигания; С – для запуска двигателя придется включать зажигание не более трех раз.
двигатель начнет работать при i -ом включении зажигания. Событие В состоит в том, что двигатель начнет работать при третьем включении зажигания; С – для запуска двигателя придется включать зажигание не более трех раз.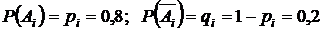 .
.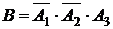 и вероятность этого события равна
и вероятность этого события равна .
.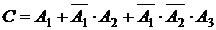 и, следовательно, вероятность события С
и, следовательно, вероятность события С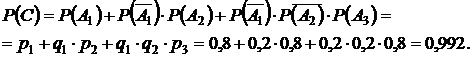
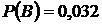 ;
; 
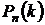 .
.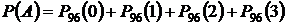 .
.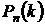 разными способами.
разными способами.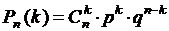 ,
,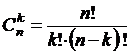 ,
, 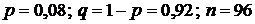 .
.
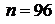 ,
,  и
и 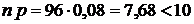 , то искомую вероятность можно вычислить по приближенной формуле Пуассона
, то искомую вероятность можно вычислить по приближенной формуле Пуассона 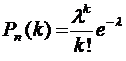 , где
, где 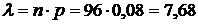 .
.
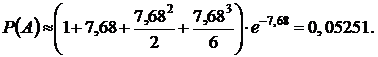
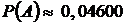 , б)
, б) 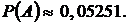
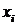
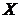 задана законом распределения.
задана законом распределения.
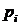


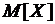 ,
, 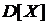 ;
;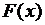 и построить ее график;
и построить ее график;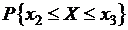 ;
; . Вычислить
. Вычислить  ,
, 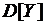 дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно по составленному закону распределения.
дважды, используя свойства (по результатам предыдущих пунктов) и непосредственно по составленному закону распределения.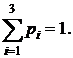 Отсюда получаем
Отсюда получаем 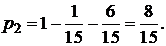
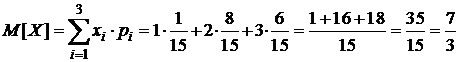 .
.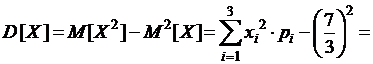
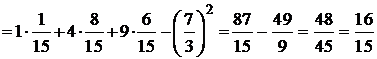 .
.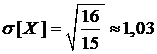 .
.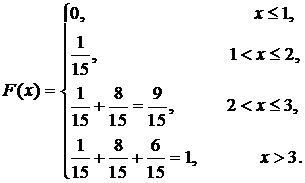

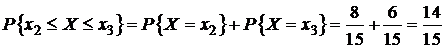 .
.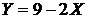 – дискретная СВ. Составим для нее ряд распределения:
– дискретная СВ. Составим для нее ряд распределения: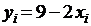
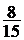
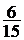
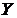 , используя составленный ряд:
, используя составленный ряд: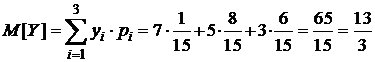 .
.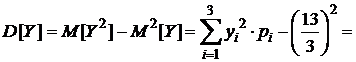
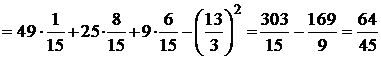 .
. .
.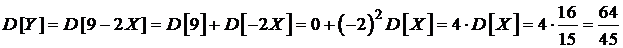 .
.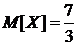 ,
, 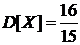 ,
, 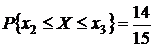 ,
, 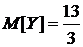 ,
,  .
.
 Найти:
Найти: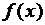 ;
;
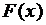 и построить ее график;
и построить ее график;
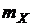 , дисперсию
, дисперсию 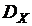 и среднее квадратическое отклонение
и среднее квадратическое отклонение 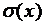 ;
;
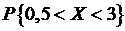 дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.
дважды, используя дифференциальную и интегральную функции. Результат проиллюстрируйте на графиках.

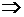
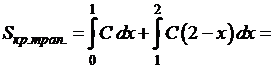
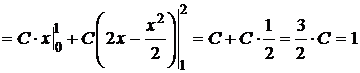
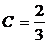 .
.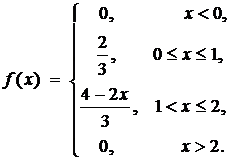

 , то
, то 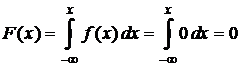 ;
;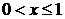 , то
, то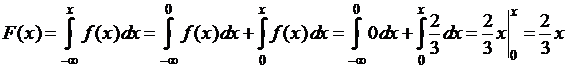 ;
;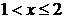 , то
, то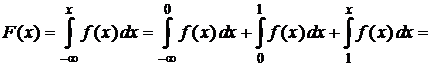
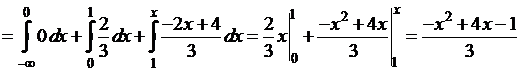 .
.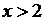 , то
, то
 .
.


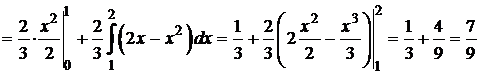 ;
;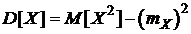 :
: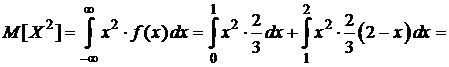
 ;
;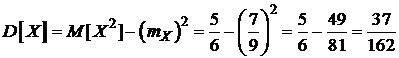 ;
;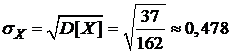 .
.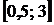 двумя способами:
двумя способами:
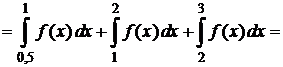
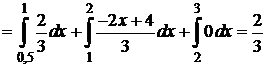 .
.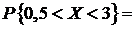
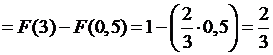 .
. (рис. 6).
(рис. 6).

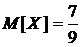 ;
; 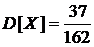 ;
;  ;
; 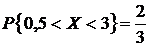 .
. ,
, 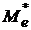 ,
,  ,
, 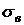 , s.
, s.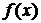 ;
;
 её теоретический аналог
её теоретический аналог  .
.
 с заданным уровнем значимости
с заданным уровнем значимости 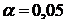 , окончательно принять или отвергнуть выдвинутую гипотезу о распределении генеральной совокупности.
, окончательно принять или отвергнуть выдвинутую гипотезу о распределении генеральной совокупности. и кривую распределения
и кривую распределения 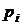 . Сравнить график
. Сравнить график  .
.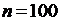 на
на 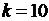 частичных интервалов равной длины и посчитаем частоты попадания наблюдаемых значений в частичные интервалы.
частичных интервалов равной длины и посчитаем частоты попадания наблюдаемых значений в частичные интервалы.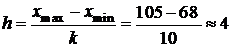 .
.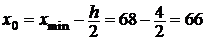 . Получим последовательность интервалов: [66; 70], (70; 74], …, (102; 106].
. Получим последовательность интервалов: [66; 70], (70; 74], …, (102; 106].
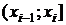

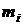
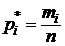
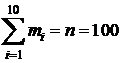 – объём выборки;
– объём выборки; 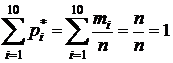 .
.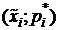 .
График полигона представлен на рис. 11.
.
График полигона представлен на рис. 11.
 Рис. 11
Рис. 11
 .
.
 Рис. 12
Рис. 12
 непрерывной случайной величины X совпадает с кумулятой (графиком накопленных частот).
непрерывной случайной величины X совпадает с кумулятой (графиком накопленных частот). на концах интервалов, и соединим их отрезками прямых (рис. 13).
на концах интервалов, и соединим их отрезками прямых (рис. 13).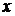

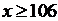
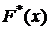

 является статистическим аналогом интегральной функции распределения
является статистическим аналогом интегральной функции распределения 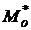 находится внутри интервала, для которого соответствующая частота максимальна. В нашем случае
находится внутри интервала, для которого соответствующая частота максимальна. В нашем случае 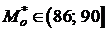 , при этом
, при этом 
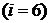 .
.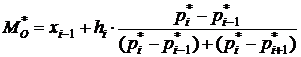 ,
,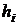 – длина частичного интервала
– длина частичного интервала  ,
,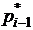 – частость, соответствующая предыдущему частичному интервалу
– частость, соответствующая предыдущему частичному интервалу 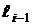 ,
,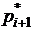 – частость, соответствующая следующему частичному интервалу
– частость, соответствующая следующему частичному интервалу 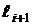 .
.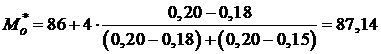 .
.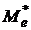 интервального вариационного ряда принадлежит тому частотному интервалу, для которого накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины всей суммы частот. Геометрически прямая
интервального вариационного ряда принадлежит тому частотному интервалу, для которого накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины всей суммы частот. Геометрически прямая  делит площадь гистограммы пополам.
делит площадь гистограммы пополам.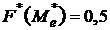 . Для данного вариационного ряда значение
. Для данного вариационного ряда значение 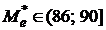 .
.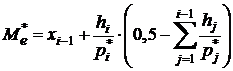 .
. .
.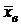 , выборочной дисперсии
, выборочной дисперсии 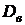 , выборочного среднего квадратического отклонения
, выборочного среднего квадратического отклонения 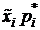
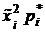
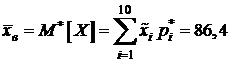 ;
; ;
;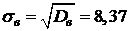 ;
; ;
;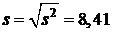 .
.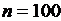 достаточно велико, то вместо
достаточно велико, то вместо 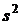 можно использовать неисправленную выборочную дисперсию
можно использовать неисправленную выборочную дисперсию  .
.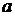 является средняя выборочная
является средняя выборочная  ; точечной оценкой генерального среднего квадратического отклонения
; точечной оценкой генерального среднего квадратического отклонения  является исправленное выборочное среднее квадратическое отклонение, т. е.
является исправленное выборочное среднее квадратическое отклонение, т. е. 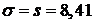 .
.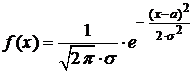 нормального распределения непрерывной случайной величины
нормального распределения непрерывной случайной величины 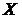 .
. (рис. 14).
(рис. 14).
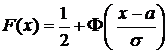 нормального распределения. Построим на одном чертеже с эмпирической функцией
нормального распределения. Построим на одном чертеже с эмпирической функцией  ,
, 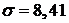 (рис. 15).
(рис. 15).
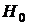 : «Генеральная совокупность распределена по нормальному закону с параметрами
: «Генеральная совокупность распределена по нормальному закону с параметрами  : «Генеральная совокупность не распределена по нормальному закону».
: «Генеральная совокупность не распределена по нормальному закону».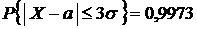 ,
,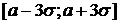 .
.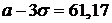 ,
, 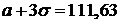 , отсюда получаем, что интервал опытных данных
, отсюда получаем, что интервал опытных данных 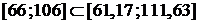 . Таким образом, найденный промежуток полностью накрыл наши статистические значения.
. Таким образом, найденный промежуток полностью накрыл наши статистические значения.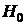 опытным данным.
опытным данным. и выравнивающие частоты
и выравнивающие частоты  .
. ). Т. к. число наблюдений в крайних интервалах меньше 5, то объединим их с соседними. Получим следующий ряд распределения:
). Т. к. число наблюдений в крайних интервалах меньше 5, то объединим их с соседними. Получим следующий ряд распределения: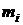
 . Т. к. случайная величина определена на интервале
. Т. к. случайная величина определена на интервале  , то крайние промежутки в ряде распределения заменяем, соответственно на
, то крайние промежутки в ряде распределения заменяем, соответственно на  и
и 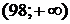 (рис. 16).
(рис. 16).
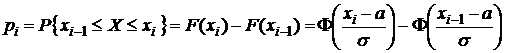 .
.
 ;
;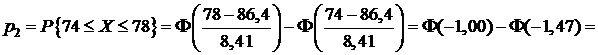
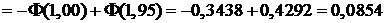 ;
;
 ;
;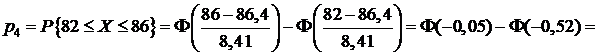
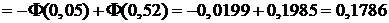 ;
;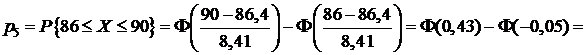
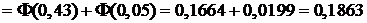 ;
;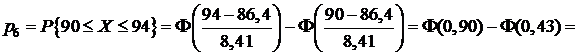
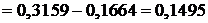 ;
;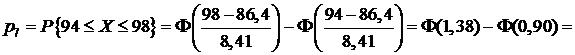
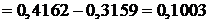 ;
;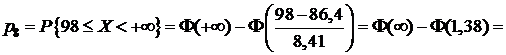
 .
.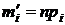
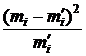
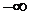 ; 74]
; 74]
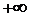 )
)
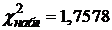 .
.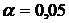 и числу степеней свободы
и числу степеней свободы 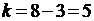 найдём критическое значение
найдём критическое значение  .
. , то нет оснований отвергнуть проверяемую нулевую гипотезу. Т. е. принимаем предположение, что статистические данные распределены по нормальному закону с параметрами
, то нет оснований отвергнуть проверяемую нулевую гипотезу. Т. е. принимаем предположение, что статистические данные распределены по нормальному закону с параметрами 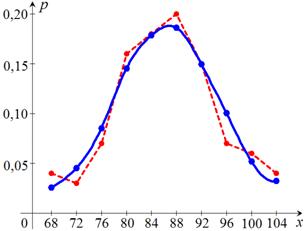
 – кривая
– кривая  – кривая
– кривая 



