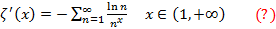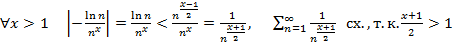Вопрос 1
Опр. 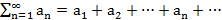 наз. числовой ряд.
наз. числовой ряд.
 ;
; 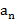 – n-ый член ряда.
– n-ый член ряда.
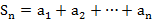 – n-ая частичная сумма;
– n-ая частичная сумма;  – последовательность частичных сумм
– последовательность частичных сумм
Опр. Если 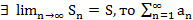 наз. сх-ся, а S наз. его суммой:
наз. сх-ся, а S наз. его суммой:  .
.
Если 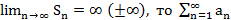 наз. расх-ся,
наз. расх-ся,  . Если
. Если  , то
, то 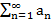 наз. расх-ся.
наз. расх-ся.
Линейные свойства сх. рядов:
1. 
2. 

Сочетательное свойство

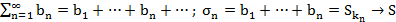 , т.е.
, т.е. 
Скобки можно расставлять только в сходящемся ряде!!!
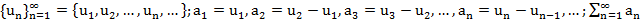

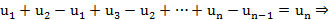 двусторонняя связь между рядами и последовательностями
двусторонняя связь между рядами и последовательностями
Вопрос 2
(Критерий Коши для посл-ти)
Посл-ть  .
.
(Критерий Коши для рядов)
Ряд  .
.
Утв. (Необх. признак сх-ти ряда) Пусть 
Док-во: 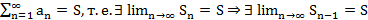 ;
; 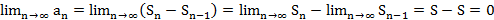
Знакоположительные числовые ряды
Опр. 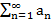 наз. знакополож., если
наз. знакополож., если  .
.
Т1.  – сх.
– сх. 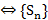 – огр. сверху, при этом
– огр. сверху, при этом 
Док-во: 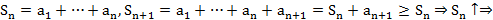 по теор. для посл. (1 сем.)
по теор. для посл. (1 сем.) 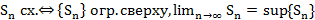
Вопрос 3
Т2. (Признак сравнения) 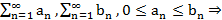
1. 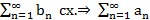 сх.
сх.
2. 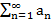 расх.
расх. 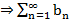 расх.
расх.
Док-во:
1. 
2.  сх. Тогда по св-ву 1
сх. Тогда по св-ву 1 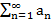 тоже сх., но по усл.
тоже сх., но по усл. 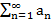 расх.
расх.  противоречие
противоречие 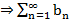 расх.
расх.
Сл. (Признак сравнения в предельной форме)
 сх. или расх. одновр.
сх. или расх. одновр.
Док-во:
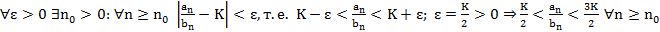
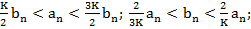 Предп., что
Предп., что 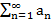 сх.
сх.  тоже сх.
тоже сх. 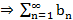 сх.
сх.
Пусть 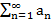 расх.
расх. 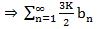 тоже расх.
тоже расх.  тоже расх.
тоже расх.
Аналогично для сх. и расх.  .
.
Вопрос 4
Т3. (Интегральный признак Коши-Маклорена)
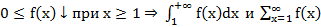 сх. или расх. одновременно.
сх. или расх. одновременно.
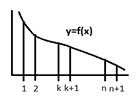 Док-во:
Док-во:

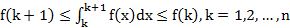
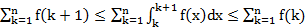
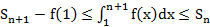
Если ряд сх., то 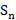 имеет огр. сверху част. суммы
имеет огр. сверху част. суммы  огр. сверху той же суммой
огр. сверху той же суммой  сх. Если ряд расх., то
сх. Если ряд расх., то 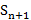 не огр. сверху,
не огр. сверху, 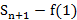 тоже
тоже  не огр.
не огр. 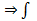 расх.
расх.
Если  сх., то
сх., то 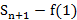 огр. сверху
огр. сверху 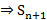 огр. сверху
огр. сверху  ряд сх. Если
ряд сх. Если  расх., то
расх., то 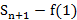 не огр. сверху
не огр. сверху 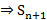 не огр. сверху
не огр. сверху 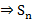 не огр. сверху
не огр. сверху  ряд расх.
ряд расх.
Вопрос 4
Т4. (Признак Даламбера) 
1. 
2. 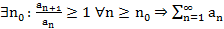 расх.
расх.
Док-во:
1. 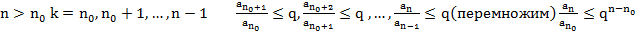
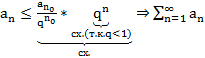 сх.
сх.
2. 
 расх.
расх.
Сл. (Признак Даламбера в пред. форме) 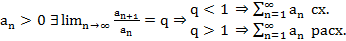
Док-во: 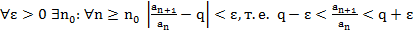
q<1 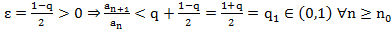
q>1 
Вопрос 6
Т5. (Радикальный признак Коши) 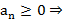
1. 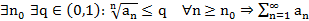 сх.
сх.
2. 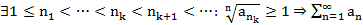 расх.
расх.
Док-во:
1.  сх.
сх.
2.  расх.
расх.
 Сл. (Радикальный признак Коши в пред. форме)
Сл. (Радикальный признак Коши в пред. форме) 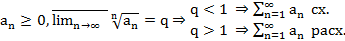
Док-во:
q<1 (крайняя правая пред. точка) Правее q+  нах. конечное число точек посл-ти. Если бы там было бескон. число точек, то м.б. бы выбрать сх. посл-ть и она лежала бы правее q, но q – верхний предел. Следовательно, противоречие.
нах. конечное число точек посл-ти. Если бы там было бескон. число точек, то м.б. бы выбрать сх. посл-ть и она лежала бы правее q, но q – верхний предел. Следовательно, противоречие.
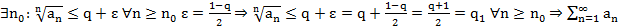 сх.
сх.
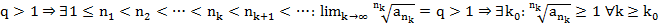
 расх.
расх.
Вопрос 7
Т6. (Специальный признак сравнения) 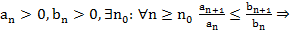
1. 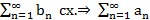 сх.
сх.
2. 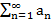 расх.
расх. 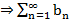 расх.
расх.
Док-во: 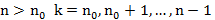
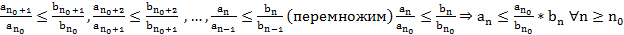
Т7. (Признак Раабе) 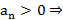
1.  сх.
сх.
2.  расх.
расх.
Док-во:
1. 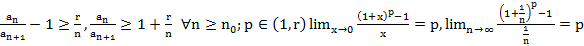 , т.е.
, т.е.
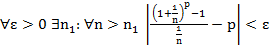 , т.е.
, т.е. 

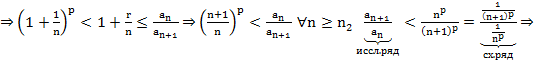 по Т6 (спец. признак сравнения)
по Т6 (спец. признак сравнения) 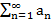 сх.
сх.
2. 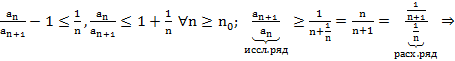 по Т6 (спец. признак сравнения)
по Т6 (спец. признак сравнения) 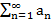 расх.
расх.
Сл. (Признак Рабье в пред. форме) 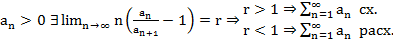
Док-во:
r – конечное число
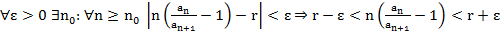
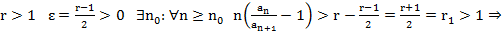 сх. по т. Раабе
сх. по т. Раабе
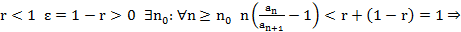 расх. по Раабе
расх. по Раабе

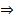 сх. по т. Раабе
сх. по т. Раабе
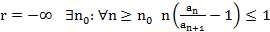
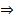 расх. по т. Раабе
расх. по т. Раабе
Т8. (Признак Гауса) 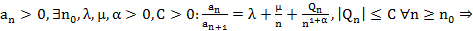
1. 
2. 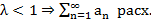
3. 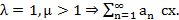
4. 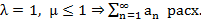
(Без доказательства!)
Связь признаков Даламбера, Раабе и Гаусса
Вопрос 8
Знакопеременные числовые ряды
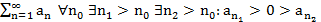
Опр. 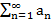 наз. абс. сх-ся, если
наз. абс. сх-ся, если 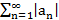 сх.
сх.
Т1. Если 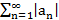 сх.
сх. 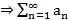 сх.
сх.
Док-во: 
Опр. Если 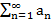 сх., но
сх., но 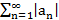 расх., то
расх., то 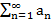 наз. усл. сх-ся.
наз. усл. сх-ся.
Вопрос 9
Т2. (Признак Лейбница) 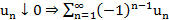 сх.
сх.
Док-во: 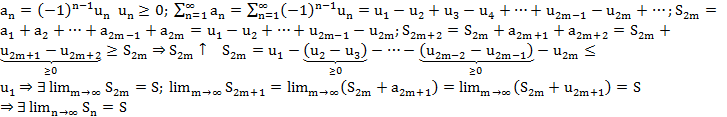
Сл. (Оценка остатка знакочер. рядов) 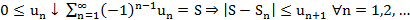


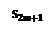
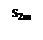




 Док-во:
Док-во: 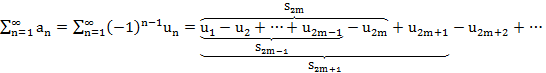
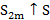
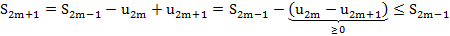

Вопрос 10
Преобразование Абеля


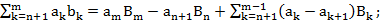

Т3. (Признак Дирихле) 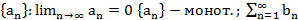 имеет огр. част. суммы
имеет огр. част. суммы 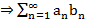 сх.
сх.
Док-во: Пусть 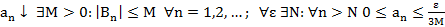
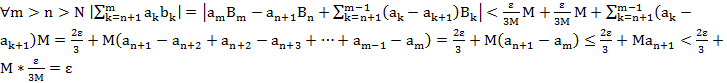
Вопрос 11
Преобразование Абеля


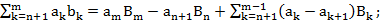

Т4. (Признак Абеля) 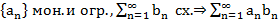 сх.
сх.
Док-во: 
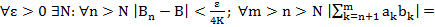

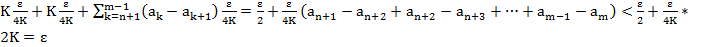
Вопрос 12
Методы суммирования
Опр. 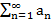 . Если
. Если  метод суммирования.
метод суммирования.
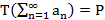 – обобщ. сумма
– обобщ. сумма
Методы суммирования (примеры):
1. 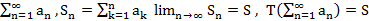
2. T 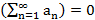
3. T 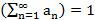
4.  (метод ср. арифм.)
(метод ср. арифм.)
Опр. Метод суммирования Т – линейный, если 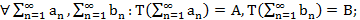
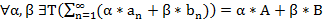
Опр. Метод суммирования Т – регулярный, если 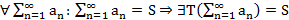
Опр. Регул. Т – вполне регулярный, если 
Метод средних арифметических линеен
Установим, что метод средних арифметических регулярный
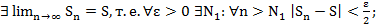

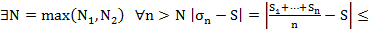
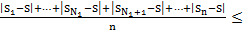
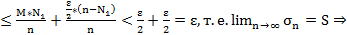 метод ср. арифм. рег.
метод ср. арифм. рег.
Установим, что этот же метод вполне рег.

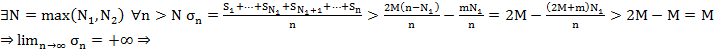 метод ср. арифм. вполне рег.
метод ср. арифм. вполне рег.
Метод ср. арифм. 2-го пор-ка сильнее, чем метод ср. арифм. 1-го пор-ка.
Вопрос 13
Равномерная сходимость.
 – определение сх-ти в каждой точке мн-ва Х (поточечная сходимость).
– определение сх-ти в каждой точке мн-ва Х (поточечная сходимость).
Опр. 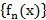 равн. сх. на мн-ве Х к f(x), если
равн. сх. на мн-ве Х к f(x), если 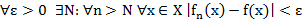
Обз.  (x) ⇉ f(x) на Х
(x) ⇉ f(x) на Х
Если  (x) ⇉ f(x) на Х ⇒
(x) ⇉ f(x) на Х ⇒  (x) → f(x) ∀х∈Х
(x) → f(x) ∀х∈Х
 Отрицание равн. сх.
Отрицание равн. сх.  (x) ⇉ f(x) на Х, если
(x) ⇉ f(x) на Х, если 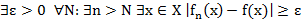
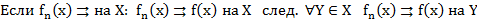
Равномерная сходимость ряда – равномерная сходимость последовательности его частичных сумм: 
Связь поточечной и равн сх
(?)Отсутствие равномерной сх-ти к поточечному пределу означает отсутствие равномерной сходимости вообще, как как если бы  (x) ⇉ g(x)
(x) ⇉ g(x) 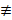 f(x) на Х, то и
f(x) на Х, то и 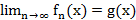 для всех
для всех 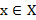
Вопрос 14
Вопрос 15
Вопрос 16
Т2’. (Критерий Коши равномерной сх-ти функц. рядов)
 ↔
↔ 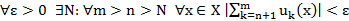 (без док-ва)
(без док-ва)
Т2’’. (Необходимый признак равномерной сх-ти функц. рядов)
 след.
след. 
Док-во:




Вопрос 17
Т3. (Признак Вейерштрасса равномерной сх-ти функц. рядов)

Док-во: 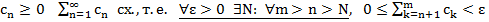

Вопрос 18
Т4. (Признак Дирихле)
 след.
след. 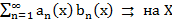
Док-во: 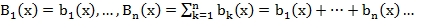
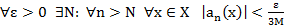
Вопрос 19
Т5. (Признак Абеля)


Док-во: 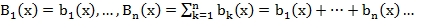

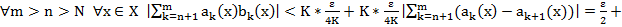

Вопрос 20
Т1. (О предельном переходе)
 (x) ⇉ f(x) на Х,
(x) ⇉ f(x) на Х, 
Док-во: 
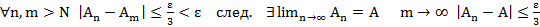
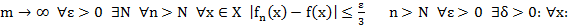

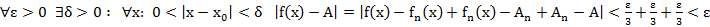
Т1’. 
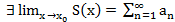
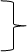 ____________________________
____________________________


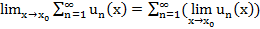
Вопрос 21
Т2(Непр. пред. ф-ии функц. посл. в точке). 
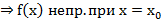
Т3. 
Док-во:  применим Т2 для каждой точки
применим Т2 для каждой точки
След. 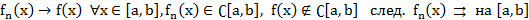
Т2’.(Непр. суммы функ. ряда в точке) 
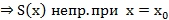
Т3’.(Непр. суммы функ. ряда на отрезке) 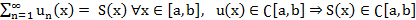
Вопрос 22
Т4.(Дини) 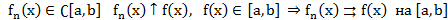
Док-во: 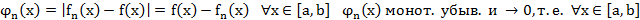
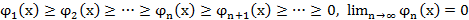
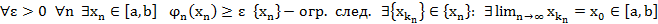

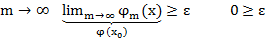
Т4’.(Дини для рядов) 
Вопрос 23
Вопрос 24
Вопрос 25
Степенные ряды
Опр. Ряды вида 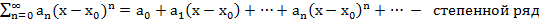

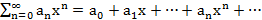
Т1. (Первая теорема Абеля)
Пусть 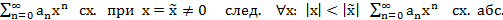
Док-во: 
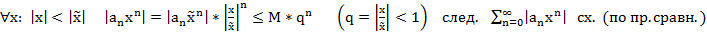

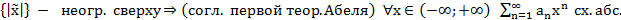
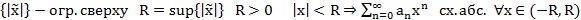
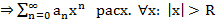
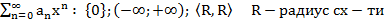

Вопрос 26
Т2. (Коши-Адамар)
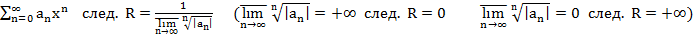
Док-во: 
1. 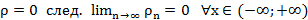

2. 

3. 

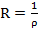
Вопрос 27
Т3. (О равномерной сходимости степенных рядов)
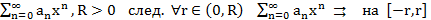
Док-во: 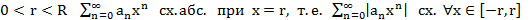
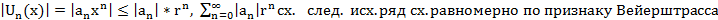
Т4. (О непрерывности суммы степенного ряда)

Док-во: 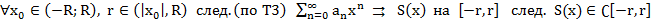
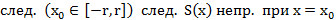
Т5. (Теорема единственности для степенных рядов)



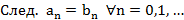
Док-во: 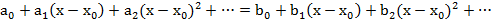
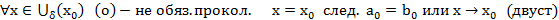
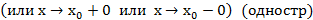

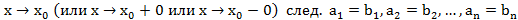
Вопрос 28
 Т6.
Т6. 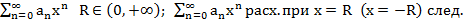
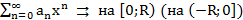
Док-во: 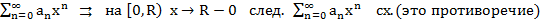
Т7. 
Док-во: 


Т8.(Вторая теорема Абеля)
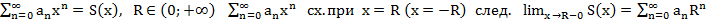
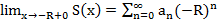
Док-во: 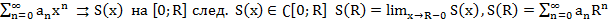
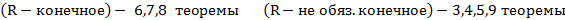
Вопрос 29
Т9.(Почленное диффер-е степенного ряда)

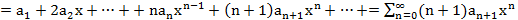
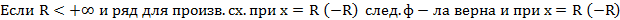
Док-во: 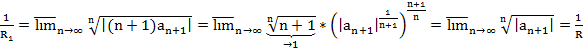
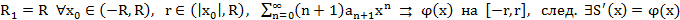

Т10.(О почленном инт. степ. ряда)



Док-во:
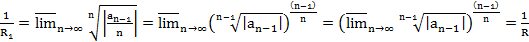
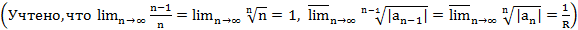
 теореме о равн. сх-ти степенного ряда
теореме о равн. сх-ти степенного ряда
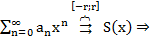 его можно интегрировать для
его можно интегрировать для 
Если 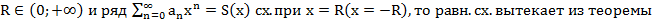 о поведении степенного ряда на концах интеграла сх.
о поведении степенного ряда на концах интеграла сх. 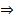 ряд можно интегрировать
ряд можно интегрировать
Вопрос 30
Биноминальный ряд
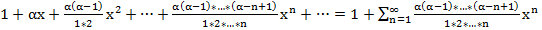

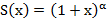


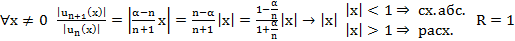
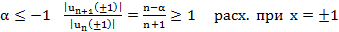
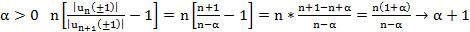

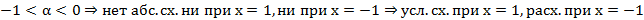
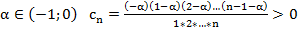
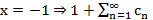 знакополож., нет абс. сх.
знакополож., нет абс. сх. 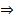 расх.
расх.
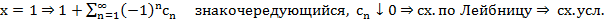
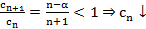

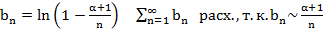
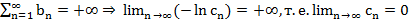
Вопрос 31

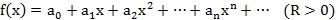
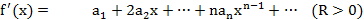

......................................................................


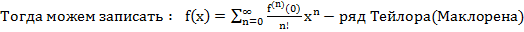


Опр. Если ф-ия 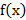 явл. суммой своего ряда Тейлора, то
явл. суммой своего ряда Тейлора, то  аналитическоя ф-ия (рассм. ф-ия должна сх. в рассм. окр-ти к
аналитическоя ф-ия (рассм. ф-ия должна сх. в рассм. окр-ти к 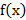 )
)
Формула Тейлора (в т. 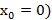

Остаточные члены:
1) 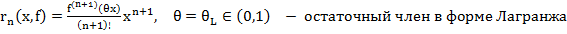
2) 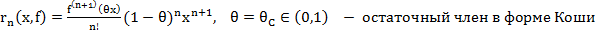
(Если остаточный член → 0, то значение формулы → 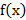 . Если остаточный член равномерно → 0, то значение формулы равномерно →
. Если остаточный член равномерно → 0, то значение формулы равномерно → 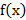 )
)
Убедимся, что 5 осн. разл. – разл-ся аналит. ф-ий.
1. 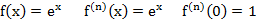
Получим ряд: 

Алгоритм: 1) нашли производные
2) построили ряд
3) уст., что ряд сх.
! 4) не факт, что он сх. именно к 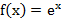
5) установим сх. ряда к 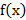
Запишем ост. член в форме Лагранжа: 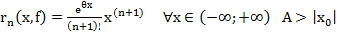


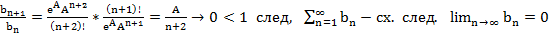
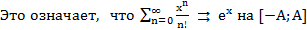
2.  (установить сам-но)!!!
(установить сам-но)!!!
3. 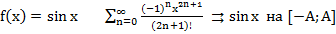 (установить сам-но)!!!
(установить сам-но)!!!
Вопрос 32

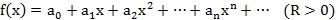
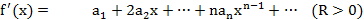

......................................................................


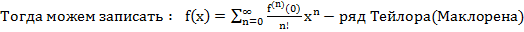


Опр. Если ф-ия 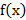 явл. суммой своего ряда Тейлора, то
явл. суммой своего ряда Тейлора, то  аналитическоя ф-ия (рассм. ф-ия должна сх. в рассм. окр-ти к
аналитическоя ф-ия (рассм. ф-ия должна сх. в рассм. окр-ти к 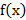 )
)
Формула Тейлора (в т. 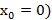

Остаточные члены:
1) 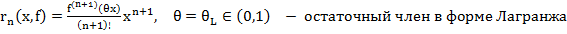
2) 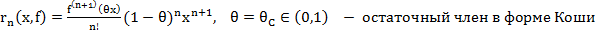
(Если остаточный член → 0, то значение формулы → 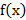 . Если остаточный член равномерно → 0, то значение формулы равномерно →
. Если остаточный член равномерно → 0, то значение формулы равномерно → 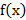 )
)
4. 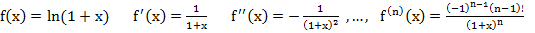

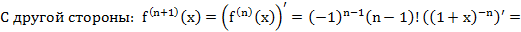
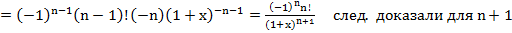
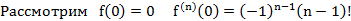
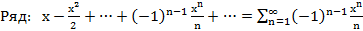
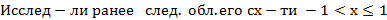
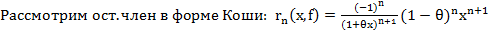
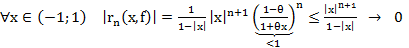


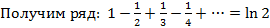
5. 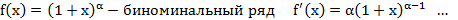









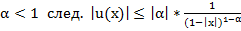
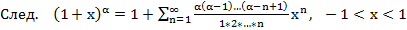
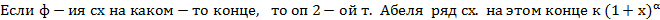
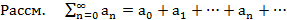
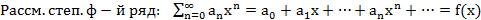
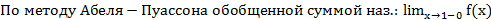

· 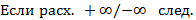
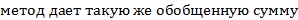
· 
Надо куда-то вставлять ли?
Пример

1. |q|<1; 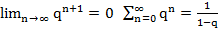 сх.
сх.
2. q>1; 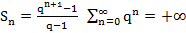 расх.
расх.
3. q<-1; 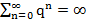 расх.
расх.
4.  расх.
расх.
5. 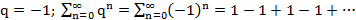 расх.
расх.
Пример
 - гармонический ряд
- гармонический ряд
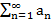 – расх.
– расх. 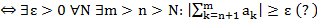

Пример


Ряд Лейбница
 расх.
расх. 
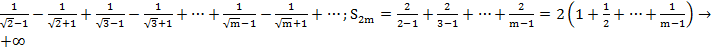
Примеры

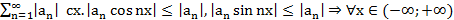 оба ряда сх. абс.
оба ряда сх. абс.

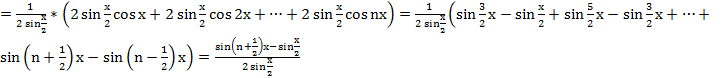
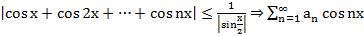 сх. усл. (по Дирихле)
сх. усл. (по Дирихле)
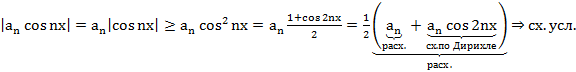
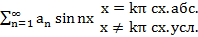
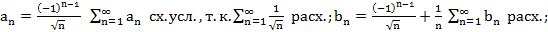
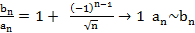
Суммирование:

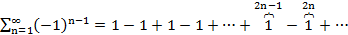

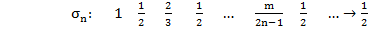

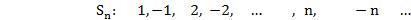

Пример.
X = 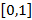
1. 
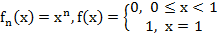 ⇉
⇉
2. 
 ⇉
⇉
3. 
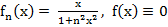 ⇉
⇉
4. 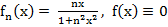 ⇉
⇉
x ≠ 0 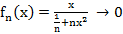
5. 
 ⇉
⇉
x ≠ 0 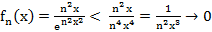
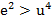
·  Установим, что в примере 1
Установим, что в примере 1  (x) ⇉ f(x)
(x) ⇉ f(x)
∃ε 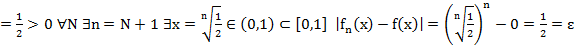
·  Установим, что в примере 2
Установим, что в примере 2  (x) ⇉ f(x)
(x) ⇉ f(x)
∃ε 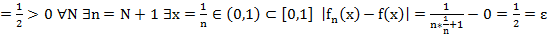
· Установим, что в примере 3  (x) ⇉ f(x)
(x) ⇉ f(x)
∀ε 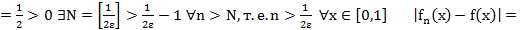
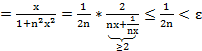
·  Установим, что в примере 4
Установим, что в примере 4  (x) ⇉ f(x)
(x) ⇉ f(x)
∃ε 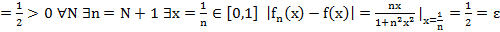
·  Установим, что в примере 5
Установим, что в примере 5  (x) ⇉ f(x)
(x) ⇉ f(x)
∃ε 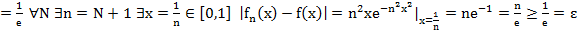
Применим эту теорему для 5 примеров.
1. 



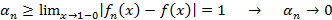 след. ⇉
след. ⇉
2.  след. ⇉
след. ⇉
3. 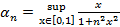
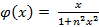
 при
при 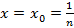
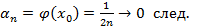 ⇉
⇉
4. 

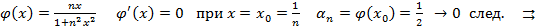
5. 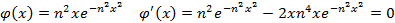
 при
при 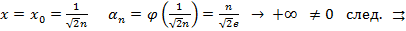
Пример. Ряд Лейбница 1 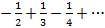
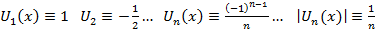

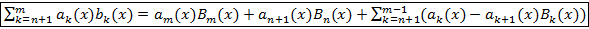


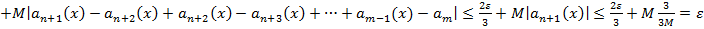

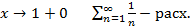
Предположим, что ⇉ есть, перейдем к пределу 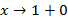 , каждый член ряда исх. стр. к соотв. члену другого ряда. Но этот другой ряд не обл. ⇉, след. исх. ряд тоже не обладает ею.
, каждый член ряда исх. стр. к соотв. члену другого ряда. Но этот другой ряд не обл. ⇉, след. исх. ряд тоже не обладает ею.
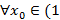 ,+∞)
,+∞) 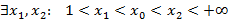





 Рассм. этот ряд не на всем мн-ве, а только на
Рассм. этот ряд не на всем мн-ве, а только на 
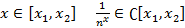

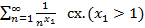 след.
след. 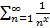 ⇉
⇉ 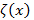 на
на 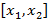 (по Вейерштрассу)
(по Вейерштрассу)
След.  след.
след. 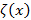 непр. при
непр. при 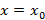 (
(
! Установим отсутствие равн. сх., а затем исп-я равн. сх. докажем непр-ть.
Установим дифф-ть.
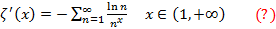
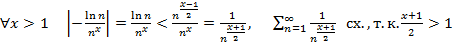

|
|
|



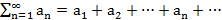 наз. числовой ряд.
наз. числовой ряд. ;
; 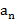 – n-ый член ряда.
– n-ый член ряда.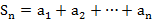 – n-ая частичная сумма;
– n-ая частичная сумма;  – последовательность частичных сумм
– последовательность частичных сумм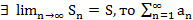 наз. сх-ся, а S наз. его суммой:
наз. сх-ся, а S наз. его суммой:  .
.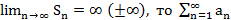 наз. расх-ся,
наз. расх-ся,  . Если
. Если  , то
, то 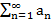 наз. расх-ся.
наз. расх-ся.



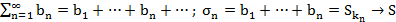 , т.е.
, т.е. 
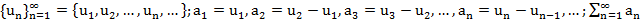

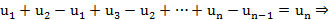 двусторонняя связь между рядами и последовательностями
двусторонняя связь между рядами и последовательностями .
. .
.
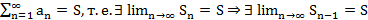 ;
; 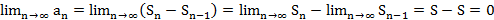
 .
. – сх.
– сх. 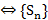 – огр. сверху, при этом
– огр. сверху, при этом 
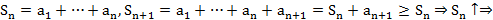 по теор. для посл. (1 сем.)
по теор. для посл. (1 сем.) 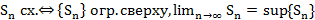
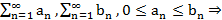
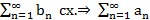 сх.
сх.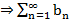 расх.
расх.
 сх. Тогда по св-ву 1
сх. Тогда по св-ву 1  противоречие
противоречие  сх. или расх. одновр.
сх. или расх. одновр.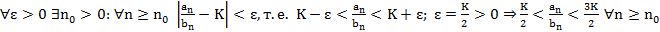
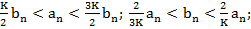 Предп., что
Предп., что  тоже сх.
тоже сх. 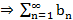 сх.
сх.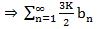 тоже расх.
тоже расх.  тоже расх.
тоже расх. .
.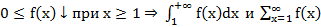 сх. или расх. одновременно.
сх. или расх. одновременно. Док-во:
Док-во:
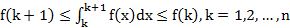
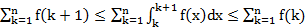
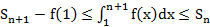
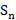 имеет огр. сверху част. суммы
имеет огр. сверху част. суммы  огр. сверху той же суммой
огр. сверху той же суммой 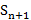 не огр. сверху,
не огр. сверху, 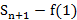 тоже
тоже 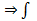 расх.
расх. сх., то
сх., то 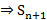 огр. сверху
огр. сверху 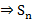 не огр. сверху
не огр. сверху 

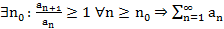 расх.
расх.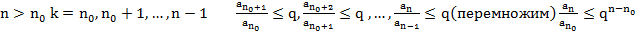
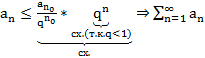 сх.
сх.
 расх.
расх. 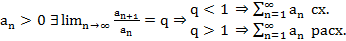
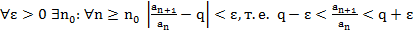
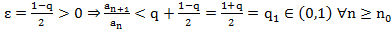

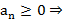
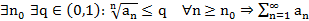 сх.
сх.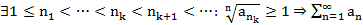 расх.
расх. сх.
сх. расх.
расх. Сл. (Радикальный признак Коши в пред. форме)
Сл. (Радикальный признак Коши в пред. форме) 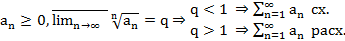
 нах. конечное число точек посл-ти. Если бы там было бескон. число точек, то м.б. бы выбрать сх. посл-ть и она лежала бы правее q, но q – верхний предел. Следовательно, противоречие.
нах. конечное число точек посл-ти. Если бы там было бескон. число точек, то м.б. бы выбрать сх. посл-ть и она лежала бы правее q, но q – верхний предел. Следовательно, противоречие.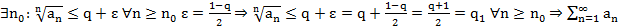 сх.
сх.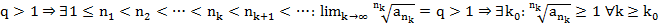
 расх.
расх.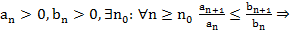
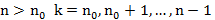
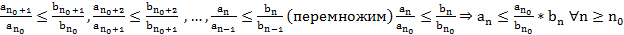
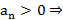
 сх.
сх. расх.
расх.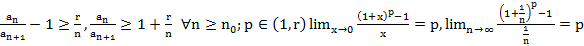 , т.е.
, т.е.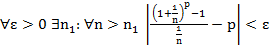 , т.е.
, т.е. 

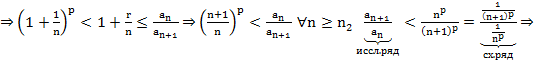 по Т6 (спец. признак сравнения)
по Т6 (спец. признак сравнения) 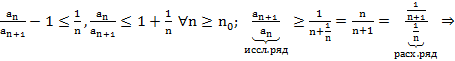 по Т6 (спец. признак сравнения)
по Т6 (спец. признак сравнения) 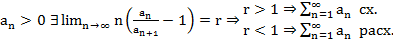
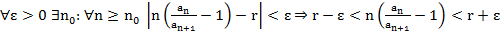
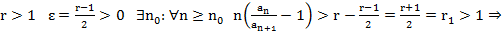 сх. по т. Раабе
сх. по т. Раабе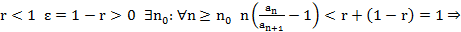 расх. по Раабе
расх. по Раабе
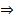 сх. по т. Раабе
сх. по т. Раабе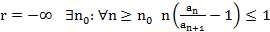
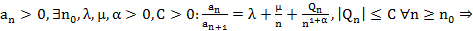

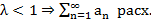
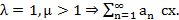
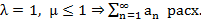
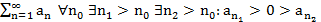
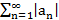 сх.
сх.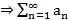 сх.
сх.
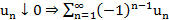 сх.
сх.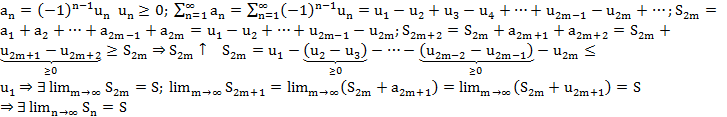
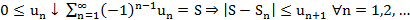


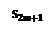
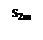




 Док-во:
Док-во: 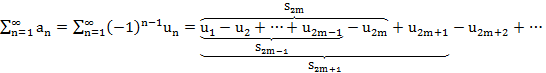
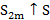
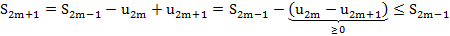



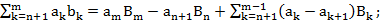

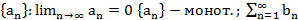 имеет огр. част. суммы
имеет огр. част. суммы 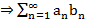 сх.
сх.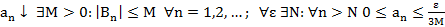
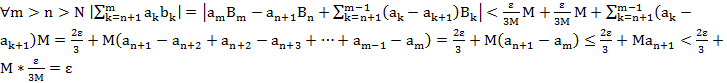
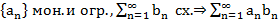 сх.
сх.
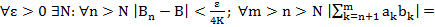

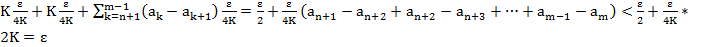
 метод суммирования.
метод суммирования.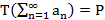 – обобщ. сумма
– обобщ. сумма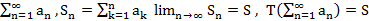
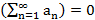
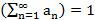
 (метод ср. арифм.)
(метод ср. арифм.)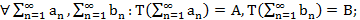
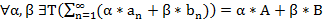
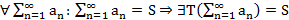

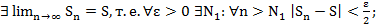

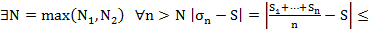
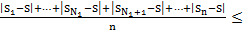
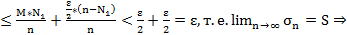 метод ср. арифм. рег.
метод ср. арифм. рег.
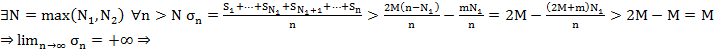 метод ср. арифм. вполне рег.
метод ср. арифм. вполне рег. – определение сх-ти в каждой точке мн-ва Х (поточечная сходимость).
– определение сх-ти в каждой точке мн-ва Х (поточечная сходимость).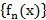 равн. сх. на мн-ве Х к f(x), если
равн. сх. на мн-ве Х к f(x), если 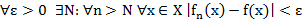
 (x) ⇉ f(x) на Х
(x) ⇉ f(x) на Х Отрицание равн. сх.
Отрицание равн. сх. 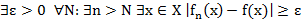
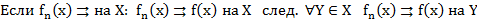

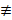 f(x) на Х, то и
f(x) на Х, то и 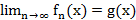 для всех
для всех 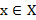
 ↔
↔ 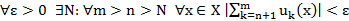 (без док-ва)
(без док-ва)





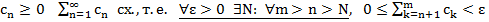

 след.
след. 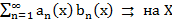
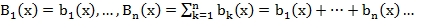
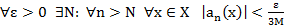



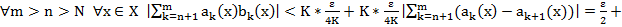



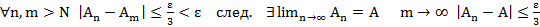
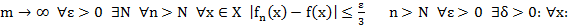

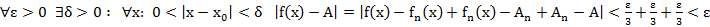

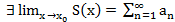
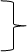 ____________________________
____________________________

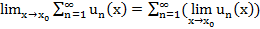

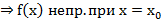

 применим Т2 для каждой точки
применим Т2 для каждой точки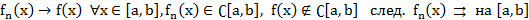

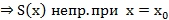
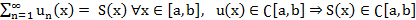
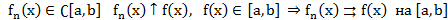
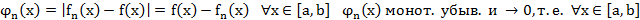
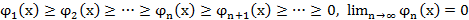
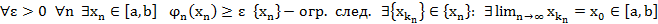

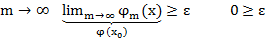

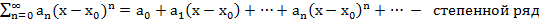

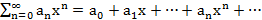
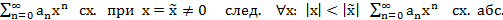

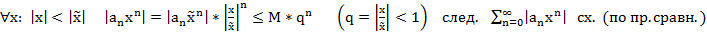

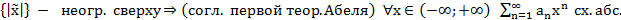
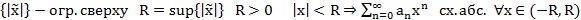
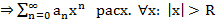
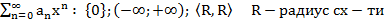

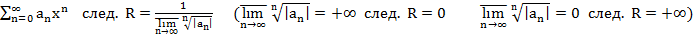

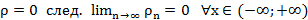





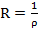
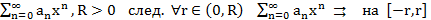
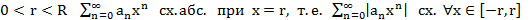
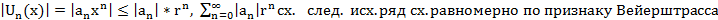

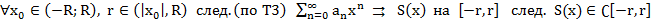
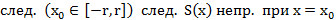



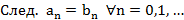
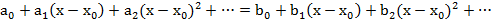
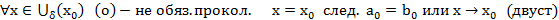
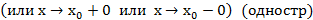

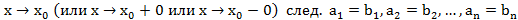
 Т6.
Т6. 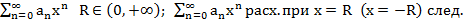
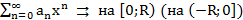
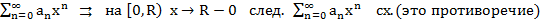




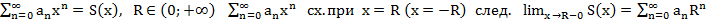
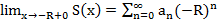
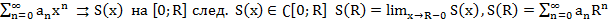
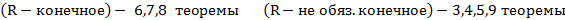

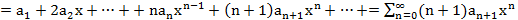
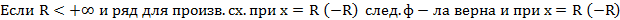
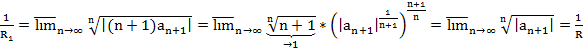
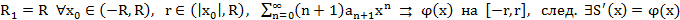




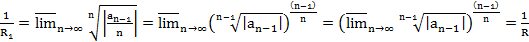
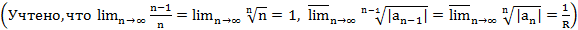
 теореме о равн. сх-ти степенного ряда
теореме о равн. сх-ти степенного ряда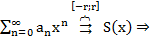 его можно интегрировать для
его можно интегрировать для 
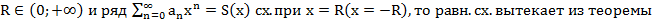 о поведении степенного ряда на концах интеграла сх.
о поведении степенного ряда на концах интеграла сх. 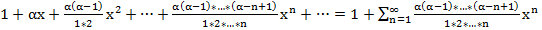

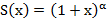


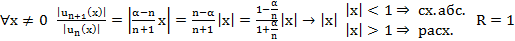
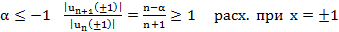
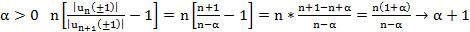

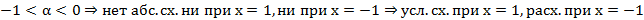
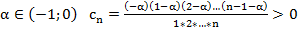
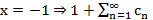 знакополож., нет абс. сх.
знакополож., нет абс. сх. 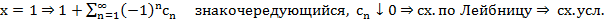
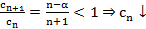

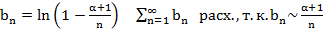
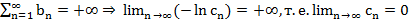

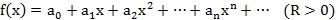
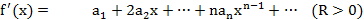



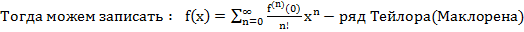


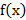 явл. суммой своего ряда Тейлора, то
явл. суммой своего ряда Тейлора, то  аналитическоя ф-ия (рассм. ф-ия должна сх. в рассм. окр-ти к
аналитическоя ф-ия (рассм. ф-ия должна сх. в рассм. окр-ти к 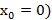

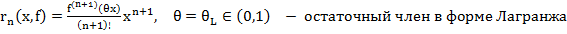
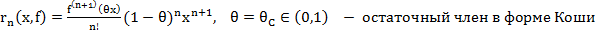
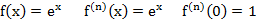


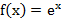
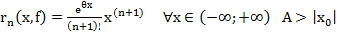


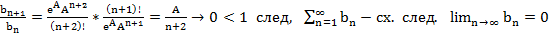
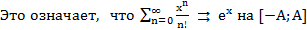
 (установить сам-но)!!!
(установить сам-но)!!!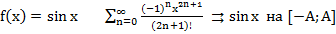 (установить сам-но)!!!
(установить сам-но)!!!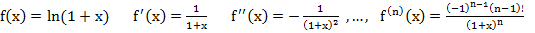

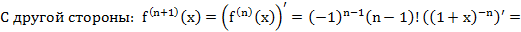
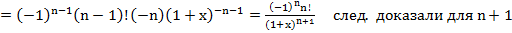
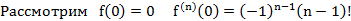
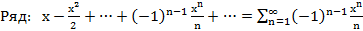
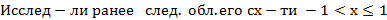
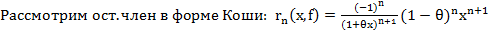
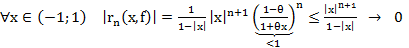


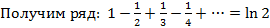
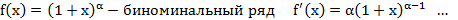









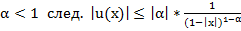
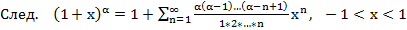
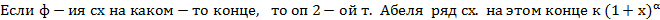
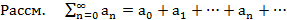
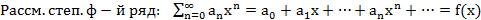
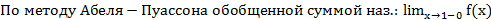

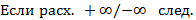
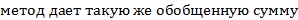


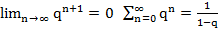 сх.
сх.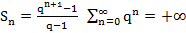 расх.
расх.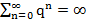 расх.
расх. расх.
расх.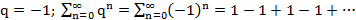 расх.
расх. - гармонический ряд
- гармонический ряд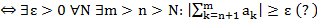



 расх.
расх. 
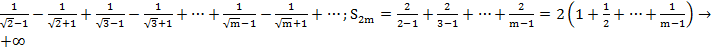

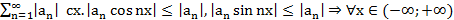 оба ряда сх. абс.
оба ряда сх. абс.
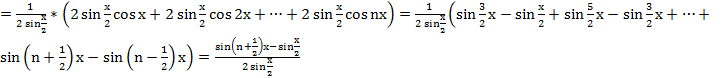
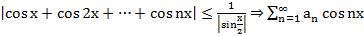 сх. усл. (по Дирихле)
сх. усл. (по Дирихле)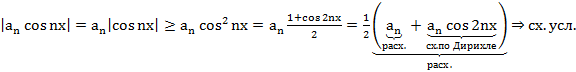
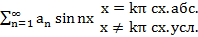
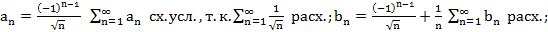
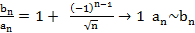

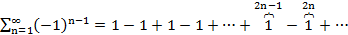

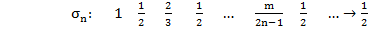

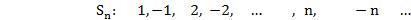

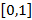

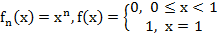 ⇉
⇉ ⇉
⇉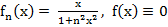 ⇉
⇉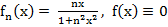 ⇉
⇉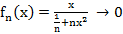

 ⇉
⇉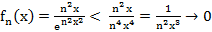
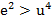
 Установим, что в примере 1
Установим, что в примере 1 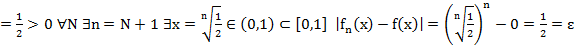
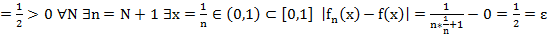
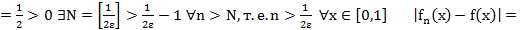
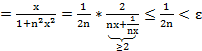
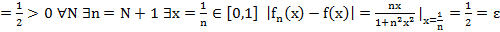
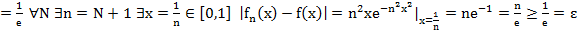




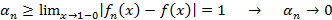 след. ⇉
след. ⇉ след. ⇉
след. ⇉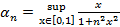
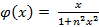
 при
при 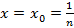
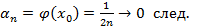 ⇉
⇉
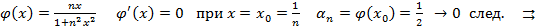
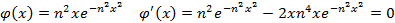
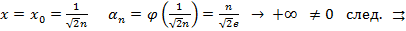
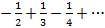
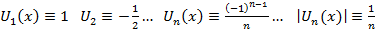

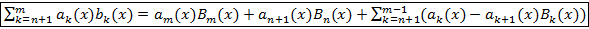


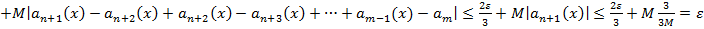

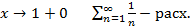
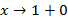 , каждый член ряда исх. стр. к соотв. члену другого ряда. Но этот другой ряд не обл. ⇉, след. исх. ряд тоже не обладает ею.
, каждый член ряда исх. стр. к соотв. члену другого ряда. Но этот другой ряд не обл. ⇉, след. исх. ряд тоже не обладает ею.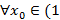 ,+∞)
,+∞) 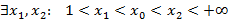






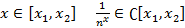

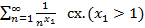 след.
след. 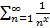 ⇉
⇉ 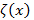 на
на 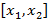 (по Вейерштрассу)
(по Вейерштрассу)  след.
след. 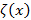 непр. при
непр. при 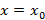 (
(