

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторным работам по дисциплине
«Компьютерная графика и 3 D визуализация»
(наименование дисциплины)
«Графика и интерфейсы»
(наименование модуля)
для студентов специальности 5 B 070400 «Вычислительная техника и программное обеспечение»
(шифр, наименование специальности)
Караганда 20 14
Лабораторная работа № 1
Построение графиков функций одной переменной
Ц е л ь р а б о т ы: получение навыков построения графиков функций и разметки координатных осей.
Задание к работе
1. Описать подпрограмму для отображения прямоугольного окна в мировой системе координат на поле вывода.
2. Описать подпрограмму для отображения прямоугольного окна в мировой системе координат на поле вывода.
3. Описать подпрограмму для определения шага разметки координатных осей, удовлетворяющего следующим требованиям:
а) мировой шаг разметки dx должен быть представлен в виде

где  ;
;
б) расстояние между засечками на экране должно быть максимально близким к заданному программистом или пользователем.
4. Описать подпрограммы для разметки координатных осей.
5. Описать подпрограмму для автоматического выбора размеров мирового окна таким образом, чтобы оно являлось прямоугольной оболочкой графика функции.
6. Описать подпрограмму для вывода на экран графика функции.
7. Составить программу для вывода на экран графиков функций, заданных явно и параметрически в табл. 3, в соответствии с номером варианта.
Содержание отчета
1. Постановка задачи.
2. Спецификации подпрограмм.
3. Описание основных алгоритмов.
|
|
4. Тексты программ.
5. Наборы тестовых данных для построения графиков.
6. Ответы на контрольные вопросы.
Методические указания
Плоскость XY основной системы координат, с которой мы до сих пор работали и которая называется мировой системой координат (МСК), совпадает с плоскостью графического экрана. Третья ось (ось Z) МСК расположена перпендикулярно экрану и направлена от экрана к нам. В качестве признака мировой системы координат пиктограмма осей имеет букву М (в английской версии — W).
Рассмотрим способы представления различных объектов.
Точка на плоскости представляется двумя числами (х, у), указывающими его положение относительно начала координат.
Прямой линиисоответствует уравнение у = kx + b. Указав параметры k и b, всегда можно отобразить бесконечную прямую линию в известной системе координат, то есть для задания прямой достаточно двух параметров.
Отрезок прямой отличается тем, что требует для описания еще двух параметров – например, координат х1 и х2 начала и конца отрезка.
Кривая второго порядка.К этому классу кривых относятся параболы, гиперболы, эллипсы, окружности, то есть все линии, уравнения которых содержат степени не выше второй. Кривая второго порядка не имеет точек перегиба.Прямые линии являются всего лишь частным случаем кривых второго порядка. Формула кривой второго порядка в общем виде может выглядеть, например, так: 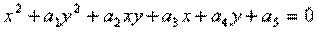 .
.
Таким образом, для описания бесконечной кривой второго порядка достаточно пяти параметров. Если требуется построить отрезок кривой, понадобятся еще два параметра.
Кривая третьего порядка.Отличие этих кривых от кривых второго порядка состоит в возможном наличии точки перегиба. Например, график функции у =х3 имеет точку перегиба в начале координат. Все кривые второго порядка, как и прямые, являются частнымислучаями кривых третьего порядка.
В общем случае уравнение кривой третьего порядка можно записать так:
 .
.
Таким образом, кривая третьего порядка описывается девятью параметрами.
|
|
Параметрическое представление кривых выбирается по целому ряду причин, в том числе потому, что зачастую объекты могут иметь вертикальные касательные. При этом аппроксимация кривой y = f(x) аналитическими функциями была бы невозможной. Кроме того, кривые, которые надо представлять, могут быть неплоскими и незамкнутыми. Наконец, параметрическое представление обеспечивает независимость представления от выбора системы координат и соответствует процессу их отображения на устройствах: позиция естественным образом определяется как две функции времени x(t) и y(t).
Варианты задании
Таблица 3
| Вариант | Функция, заданная параметрически | Функция, заданная в явном виде | |
| 1 | 2 | 3 | |
| 1 | Циклоида:
| 
| |
| 2 | Улитка Паскаля:
| 
| |
| 3 | Улитка Паскаля:
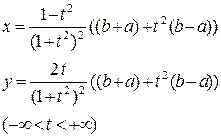
| 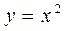
| |
| 4 | Астроида:
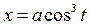
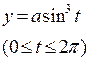
| 
| |
| 5 | Конхоида Никомеда:
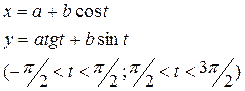
| 
| |
| Продолжение табл. 3 | |||
| 6 | Эвольвента:

| 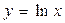
| |
| 7 | Гиперболическая спираль:
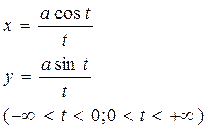
| 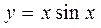
| |
| 8 | Локон Аньези:

| 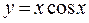
| |
| 9 | Декартов лист:
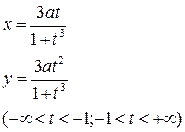
| 
| |
| 10 10 | Декартов лист:
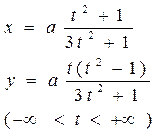
| 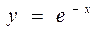
| |
| 11 | Циссоида:
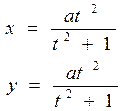
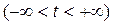
| 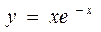
| |
|
Продолжение табл. 3 | |||
|
| Циссоида:
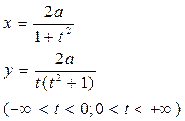
| 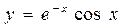
| |
| 13 | Строфоида:
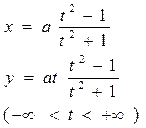
| 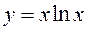
| |
| 14 | Эпициклоида:

| 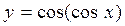
| |
| 15 | Лемниската Бернулли: 

| 
| |
П р и м е ч а н и е. В случаях, когда значение параметра t меняется в бесконечных пределах, т.е. - 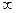 < t <+
< t <+ 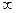 , можно произвести замену:
, можно произвести замену:
- p 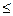 t
t 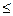 p,
p, 
где р − достаточно большие числа (подбираются экспериментально).
Контрольные вопросы:
1. Что такое мировые координаты?
2. Основные принципы разметки координатных осей.
3. Автоматический выбор размеров окна для получения целостного
изображения данного объекта.
Построение проекций тел
Ц е л ь р а б о т ы: получение навыков в построении параллельных и центральных проекций.
Задание к работе
1. Изучить классификацию проекций.
2. Подобрать подходящие структуры данных для хранения многогранников.
3. Разработать алгоритм и составить программу для получения на экране одной из четырех проекций, расположенных как показано на рисунке 8.1.
| Фронтальная | Профильная |
| Горизонтальная | Проекция по вы- бору пользователя |
Рисунок 8.1 - Расположение проекций
В четвертой четверти по выбору пользователя может быть выведена одна из следующих проекций:
|
|
а) изометрическая;
б) центральная (с указанием центра проектирования) и др.
Содержание отчета
1. Постановка задачи.
2. Спецификации подпрограмм.
3. Описание основных алгоритмов.
4. Тексты программ.
5. Ответы на контрольные вопросы.
Методические указания
Плоскость, на которую осуществляется проектирование, называется проекционной или картинной плоскостью.
Часть пространства со всеми находящимися внутри нее объектами, подлежащая изображению, назовем сценой. В общем случае объекты сцены отсекаются по границам видимого объема, а затем проецируются. Проекции трехмерных объектов строят при помощи проецирующих лучей (проекторов). Проекторы выходят из одной точки, называемой центром проектирования, и проходят через каждую точку объекта. Такая проекция называется плоской геометрической проекцией.
Проекция на плоскость xOy называется фронтальной (вид спереди), на xOz - горизонтальной (вид сверху), на yOz - профильной (вид сбоку).
Соответствующие матрицы проектирования имеют вид:

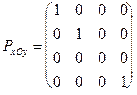
 ;
; 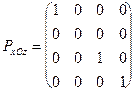 ;
; 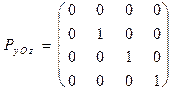
В техническом черчении за основные плоскости проекций принимают шесть граней куба (рис.8.2).
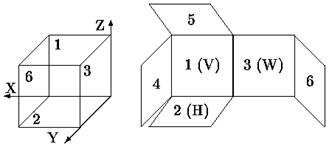
Рисунок 8.2 - Ортогональные проекции (основные виды) и их расположение на листе чертежа
1. Вид спереди, главный вид, фронтальная проекция (на заднюю грань V),
2. Вид сверху, план, горизонтальная проекция (на нижнюю грань H),
3. Вид слева, профильная проекция (на правую грань W),
4. Вид справа (на левую грань),
5. Вид снизу (на верхнюю грань),
6. Вид сзади (на переднюю грань).
По расположению центра проекции относительно плоскости проекции различаются центральная и параллельные проекции.
При параллельной проекции центр проекции находится на бесконечном расстоянии от плоскости проекции. При параллельном проектировании проекторы параллельны. Проекторы представляют собой пучок параллельных лучей. В этом случае необходимо задавать направление проецирования и расположение плоскости проекции. По взаимному расположению проекторов, плоскости проекции и главных осей координат различаются ортогональные, прямоугольные аксонометрические и косоугольные аксонометрические проекции.
|
|
Проекции на плоскости, параллельные координатным плоскостям, называются ортогональными, иначе - аксонометрическими.
При ортогональной проекции проекторы перпендикулярны плоскости проекции, а плоскость проекции перпендикулярна главной оси. Т.е. проекторы параллельны главной оси.
При аксонометрической проекции имеется одна из двух перпендикулярностей:
- при прямоугольной аксонометрической проекции проекторы перпендикулярны плоскости проекции, которая расположена под углом к главной оси;
- при косоугольной аксонометрической проекции проекторы не перпендикулярны плоскости проекции, но плоскость проекции перпендикулярна к главной оси.
При центральной проекции расстояние от центра проекции до плоскости проецирования конечно, поэтому проекторы представляют собой пучок лучей, исходящих из центра проекции. В этом случае надо задавать расположение и центра проекции, и плоскости проекции. Изображения на плоскости проекции имеют т.н. перспективные искажения, когда размер видимого изображения зависит от взаимного расположения центра проекции, объекта и плоскости проекции. Из-за перспективных искажений изображения, полученные центральной проекцией, более реалистичны, но нельзя точно передать форму и размеры. Различаются одно, двух и трехточечные центральные проекции в зависимости от того, по скольким осям выполняется перспективное искажение.
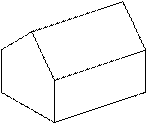
Варианты заданий
Таблица 4
| № ва- рианта | тело | № ва- рианта | тело | ||||
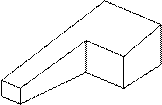 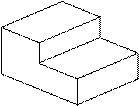 1 1
| 2 | ||||||
| 3 |
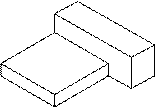
| 4 | 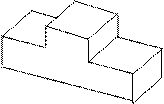
| ||||
| 5 | 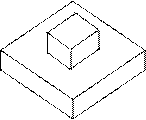
| 6 | 
| ||||
| Продолжение табл. 4 | |||||||
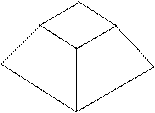 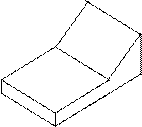 7 7
| 8 | ||||||
 9 9
| 10 | ||||||
  11 11
|
| 12 | |||||
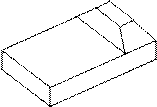 13 13
|
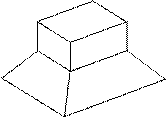
| 14 | |||||
| 15 | 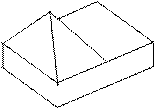
| ||||||
Контрольные вопросы
1. Определение проектирования.
2. Что такое проекция объекта?
3. Классификация проекций.
4. Параллельное проектирование и его свойства.
5. Центральное проектирование и его свойства.
6. Получение ортогональных проекций.
Лабораторная работа № 4
Преобразование изображений
Ц е л ь р а б о т ы: овладение методами преобразования изображений.
Задание к работе
1. Изучить возможности использования однородных координат для преобразования точек и прямых на плоскости.
2. Рассмотреть частные случаи преобразований:
а) параллельный перенос;
б) поворот на угол 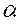 вокруг начала координат;
вокруг начала координат;
в) симметрия относительно точки;
г) симметрия относительно оси;
д) масштабирование.
3. Аппроксимировать многоугольником заданную фигуру (в соответствии с номером варианта). Составить программу, позволяющую выполнять перечисленные в п. 2 преобразования полученного многоугольника.
|
|
Содержание отчета
1. Постановка задачи.
2. Спецификации подпрограмм.
3. Описание основных алгоритмов.
4. Тексты программ.
5. Ответы на контрольные вопросы.
Методические указания
К геометрическим преобразованиям относятся преобразования сдвига, масштабирования и поворота. В связи с существенно дискретным характером изображения при выполнении этих преобразований имеется ряд особенностей.
Преобразование сдвига реализуется наиболее просто и заключается в переписывании части изображения (bitblt-операции – Bit Block Transfer). При этом возможно исполнение некоторых операций над старым и новым пикселями с одинаковыми координатами.
Наиболее употребляемыми являются:
· замена – новый пиксель просто заменяет старый,
· исключающее ИЛИ – в видеопамять заносится результат операции XOR над старым и новым кодами пикселей. Эта операция обычно используется дважды – вначале для занесения некоторого изображения, например, перекрестия и повторного его занесения для восстановления исходной картины.
Принято различать два типа преобразования масштабирования:
· целочисленное – zoom,
· произвольное, когда коэффициент масштабирования не обязательно целое число, – transfocation.
Наиболее просто реализуется целочисленное масштабирование. При увеличении в K раз каждый пиксель в строке дублируется К раз и полученная строка дублируется К раз. При уменьшении в K раз из каждой группы в K строк выбирается одна строка и в ней из каждой группы в K пикселей берется один пиксель в качестве результата. Не целочисленное масштабирование требует нерегулярного дублирования при увеличении и выбрасывания при уменьшении. Для отсутствия "дырок" в результирующем изображении при любых преобразованиях растровых картин следует для очередного пиксела результирующего изображения определить соответствующие пиксели исходного изображения, вычислить значение пикселя и занести его.
Определенные проблемы, связанные с дискретным характером изображения, возникают и при преобразовании поворота растровой картины на угол, не кратный 90o. Здесь возможны два подхода:
· Сканируются строки исходной картины, при этом вычисляются новые значения координат пикселей для результирующей картины. Ясно, что отсутствие дырок на результирующем изображении может быть обеспечено только при использовании вещественной арифметики, кроме этого возможно повторное занесение пикселей.
· Сканируются строки результирующей картины и по координатам очередного пикселя определяются координаты пикселя из исходного изображения. Этот подход гарантирует отсутствие дырок, кроме того, исключает повторное занесение пикселей.
Используются два основных способа формирования геометрических элементов моделей – это построение по заданным отношениям (ограничениям) и построение с использованием преобразований.
Рассмотрим построение с использованием преобразований.
Построение нового объекта с использованием преобразований заключается в следующем:
- задается преобразуемый объект;
- задается преобразование (это может быть обычное аффинное преобразование, определяемое матрицей, или некоторое деформирующее преобразование, например, замена одного отрезка контура ломаной);
- выполнение преобразования; в случае аффинного преобразования для векторов всех характерных точек преобразуемого объекта выполняется умножение на матрицу; для углов вначале переходят к точкам и затем выполняют преобразование.
Варианты заданий
1. Король (шахматная фигура). 9. Зонтик.
2. Пешка (» »). 10. Ваза.
3. Ферзь (» »). 11. Лопата.
4. Ладья (» »). 12. Груша.
5. Слон (» »). 13. Лодка с парусом.
6. Рыба. 14. Шляпа.
7. Ель. 15. Корзинка.
8. Корона.
Контрольные вопросы:
1. Перечислите базовые преобразования плоскости.
2. Понятие однородных координат на плоскости.
3. Как задается перспективное преобразование плоскости?
4. Определение проективно-афинного преобразования.
5. Как выглядит матрица для преобразования поворота, масштабирования, сдвига?
Лабораторная работа № 5
Растровые алгоритмы
Ц е л ь р а б о т ы: овладение методами разложения в растр отрезков и кривых второго порядка.
Задание к работе
1. Изучить алгоритмы вычерчивания отрезков (метод цифрового дифференциального анализатора и метод Брезенхема).
2. Составить программу для вывода на экран отрезка.
3. Подобрать тестовые данные для построения различно ориентированных отрезков.
4. Изучить алгоритмы Брезенхема для генерации окружности и эллипса.
5. Составить программу для построения окружности. Учесть коэффициент сжатия изображения.
6. Составить программу для построения эллипса.
Содержание отчета
1. Постановка задачи.
2. Спецификации подпрограмм.
3. Описание основных алгоритмов.
4. Тексты программ.
5. Наборы тестовых данных для построения отрезка.
6. Ответы на контрольные вопросы.
Методические указания
Требования, предъявляемые к алгоритмам вычеркивания отрезков: отрезок должен выглядеть прямым и неразрывным, начинаться и заканчиваться в заданных точках, яркость вдоль отрезка должна быть постоянной, не зависящей от длины и угла наклона. Рисование должно выполняться быстро, не все требования могут быть полностью удовлетворены, так как сама природа растрового дисплея не позволяет получать абсолютно прямые линии, кроме вертикальных и горизонтальных. Яркость зависит от наклона, т.к. она определяется расстоянием между соседними пикселами. Ускоряет процесс построения отрезка использование целочисленной арифметики.
С помощью цифрового дифференциального анализатора (ЦДА) решается дифференциальное уравнение отрезка, имеющее вид:

где Py = Yk – Yn – приращение координат отрезка по оси Y;
а Px = Xk – Xn – приращение координат отрезка по оси X.
При этом ЦДА формирует дискретную аппроксимацию непрерывного решения этого дифференциального уравнения.
В обычном ЦДА, используемом, как правило, в векторных устройствах, тем или иным образом определяется количество узлов N, используемых для аппроксимации отрезка. Затем за N циклов вычисляются координаты очередных узлов: X0 = Xn; Xi+1 = Xi + Px / N;
Y0 = Yn; Yi+1 = Yi + Py / N.
Получаемые значения Xi, Yi преобразуются в целочисленные значения координаты очередного подсвечиваемого пиксела либо округлением, либо отбрасыванием дробной части.
Генератор векторов, использующий этот алгоритм, имеет тот недостаток, что точки могут прописываться дважды, что увеличивает время построения.
Кроме того, из-за независимого вычисления обеих координат нет предпочтительных направлений, и построенные отрезки кажутся не очень красивыми.
Субъективно лучше смотрятся векторы с единичным шагом по большей относительной координате (несимметричный ЦДА). Для Px > Py (при Px, Py > 0) это означает, что координата по X направлению должна увеличиться на 1 Px раз, а координата по Y-направлению должна также Px раз увеличиться, но на Py/Px.
Т.е. количество узлов аппроксимации берется равным числу пикселей вдоль наибольшего приращения.
Для генерации отрезка из точки (x1, y1) в точку (x2, y2) в первом октанте (Px ³ Py ³ 0) алгоритм несимметричного ЦДА имеет вид:
1. Вычислить приращения координат:
Px = x2 – x1; Py = y2 – y1;
2. Занести начальную точку отрезка:
PutPixel (x1, y1);
3. Сгенерировать отрезок:
while (x1 < x2)
{x1:= x1 + 1.0;
y1:= y1 + Py/Px;
PutPixel (x1, y1);}
Пример генерации отрезка по алгоритму несимметричного ЦДА приведен на рис.2.1.
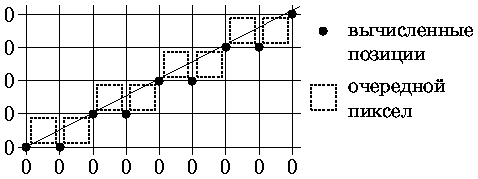
Рисунок 2.1 - Генерация отрезка несимметричным ЦДА
Так как приращения координат, как правило, не являются целой степенью двойки, то в ЦДА-алгоритме (см. предыдущий пункт) требуется выполнение деления, что не всегда желательно, особенно при аппаратной реализации.
Брезенхем предложил алгоритм, не требующий деления, как и в алгоритме несимметричного ЦДА, но обеспечивающий минимизацию отклонения сгенерированного образа от истинного отрезка, как в алгоритме обычного ЦДА. Основная идея алгоритма состоит в том, что если угловой коэффициент прямой < 1/2, то естественно точку, следующую за точкой (0,0), поставить в позицию (1,0) (рис. 2.2а), а если угловой коэффициент > 1/2, то – в позицию (1,1) (рис. 2.2б). Для принятия решения, куда заносить очередной пиксел вводится величина отклонения Е точной позиции от середины между двумя возможными растровыми точками в направлении наименьшей относительной координаты. Знак Е используется как критерий для выбора ближайшей растровой точки.
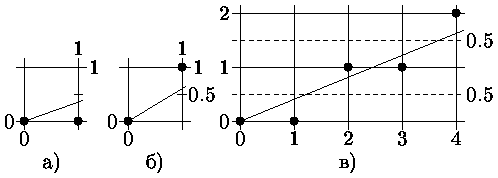
Рисунок 2.2 - Алгоритм Брезенхема генерации отрезков
Если Е < 0, то точное Y-значение округляется до последнего меньшего целочисленного значения Y, т.е. Y-координата не меняется по сравнению с предыдущей точкой. В противном случае Y увеличивается на 1.
Для вычисления Е без ограничения общности, упрощающе положим, что рассматриваемый вектор начинается в точке (0,0) и проходит через точку (4, 1.5) (см. рис. 2.2в), т.е. имеет положительный наклон, меньший 1.
Из рис. 2.2в видно, отклонение для первого шага: Е1 = Py/Px – 1/2 < 0,
поэтому для занесения пикселя выбирается точка (1,0).
Отклонение для второго шага вычисляется добавлением приращения Y-координаты для следующей X-позиции (см. рис. 2в): Е2 = Е1 + Py/Px > 0,
поэтому для занесения пикселя выбирается точка (2,1). Так как отклонение считается от Y-координаты, которая теперь увеличилась на 1, то из накопленного отклонения для вычисления последующих отклонений надо вычесть 1: Е2 = Е2 – 1.
Отклонение для третьего шага: Е3 = Е2 + Py/Px < 0,
поэтому для занесения пикселя выбирается точка (3,1).
Суммируя и обозначая большими буквами растровые точки, а маленькими – точки вектора, получаем: Е1 = y1 – 1/2 = dY/dX – ½.
Возможны случаи:
| Е1 > 0 | E1 £ 0 |
| ближайшая точка есть: | |
| X1 = X0 + 1; Y1 = Y0 + 1; | X1 = X0 + 1; Y1 = Y0; |
| E2 = Е1 + Py/Px – 1; | E2 = E1 + Py/Px. |
Так как интересует только знак Е, то можно избавиться от неудобных частных умножением E на 2×Px:
| E1 = 2×Py – Px | |
| E1 > 0: | E2 = E1 + 2×(Py – Px) |
| E1 £ 0: | E2 = E1 + 2×Py |
Таким образом, получается алгоритм, в котором используются только целые числа, сложение, вычитание и сдвиг:
X = x1; Y = y1;
Px = x2 – x1; Py = y2 – y1;
E = 2*Py – Px; I = Px;
PutPixel(X, Y); /* Первая точка вектора */
while (i= i – 1 ³ 0)
{ if (E ³ 0)
{ X = X + 1; Y = Y + 1; E = E + 2*(Py – Px); }
Else X = X + 1; E = E + 2*Py;
PutPixel(X, Y); /* Очередная точка вектора */ }
Этот алгоритм пригоден для случая 0 £ dY £ dX. Для других случаев алгоритм строится аналогичным образом.
Во многих областях приложений, таких как, например, системы автоматизированного проектирования машиностроительного направления, естественными графическими примитивами, кроме отрезков прямых и строк текстов, являются и конические сечения, т.е. окружности, эллипсы, параболы и гиперболы. Наиболее употребительным примитивом, естественно, является окружность. Один из наиболее простых и эффективных алгоритмов генерации окружности разработан Брезенхемом. Для простоты и без ограничения общности рассмотрим генерацию 1/8 окружности, центр которой лежит в начале координат. Остальные части окружности могут быть получены последовательными отражениями (использованием симметрии точек на окружности относительно центра и осей координат).
Окружность с центром в начале координат описывается уравнением:
X2 + Y2 = R2.
Алгоритм Брезенхема пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пикселя точку растра Pi(Xi, Yi), ближайшую к истинной окружности, так чтобы ошибка:
Ei(Pi) = (Xi2 + Yi2) – R2 была минимальной.
Причем, как и в алгоритме Брезенхема для генерации отрезков, выбор ближайшей точки выполняется с помощью анализа значений управляющих переменных, для вычисления которых не требуется вещественной арифметики. Для выбора очередной точки достаточно проанализировать знаки.
Рассмотрим генерацию 1/8 окружности по часовой стрелке, начиная от точки X=0, Y=R.
Проанализируем возможные варианты занесения i + 1-й точки, после занесения i-й.
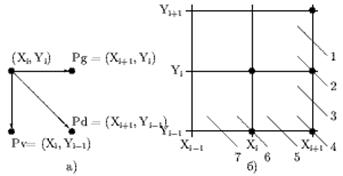
Рисунок 2.3 - Варианты расположения очередного пикселя окружности
При генерации окружности по часовой стрелке после занесения точки (Xi, Yi) следующая точка может быть (см. рис. 2.4а) либо Pg = (Xi+1, Yi) – перемещение по горизонтали, либо Pd = (Xi+1, Yi-1) – перемещение по диагонали, либо Pv = (Xi, Yi-1) – перемещение по вертикали.
Для этих возможных точек вычислим и сравним абсолютные значения разностей квадратов расстояний от центра окружности до точки и окружности: |Dg| = | (X+1)2 + Y2 – R2 |
|Dd| = | (X+1)2 + (Y-1)2 – R2 |
|Dv| = | X2 + (Y-1)2 – R2 |
Выбирается и заносится та точка, для которой это значение минимально.
Выбор способа расчета определяется по значению Dd. Если Dd < 0, то диагональная точка внутри окружности. Это варианты 1-3. Если Dd > 0, то диагональная точка вне окружности. Это варианты 5-7. И, наконец, если Dd = 0, то диагональная точка лежит точно на окружности.
Контрольные вопросы:
1. Общие требования к алгоритмам построения отрезка.
2. Принцип, положенный в основу алгоритма Брезенхема для построения линий.
3. Алгоритм Брезенхема для построения отрезка.
4. Алгоритм Брезенхема для построения окружности.
Лабораторная работа № 6
Заполнение областей
Ц е л ь р а б о т ы: освоение методов закраски областей.
Задание к работе
1. Изучить возможности графической библиотеки для получения изображений с закрашенными фигурами
2. Освоить алгоритмы закраски выпуклых, монотонных и произвольных многоугольников.
3. Освоить алгоритмы заполнения выпуклых и произвольных областей, заданных растровой разверткой границ.
4. Реализовать программно один из алгоритмов заполнения области.
Содержание отчета
1. Постановка задачи.
2. Спецификации подпрограмм.
3. Описание основных алгоритмов.
4. Тексты программ.
5. Наборы тестовых данных для построения отрезка.
6. Ответы на контрольные вопросы.
Методические указания
В большинстве приложений используется одно из существенных достоинств растровых устройств – возможность заполнения областей экрана.
Для некоторых классов геометрических фигур существуют простые алгоритмы заполнения. Например, прямоугольник можно покрыть отрезками, параллельными одной из сторон. Для построения изображения круга используем алгоритм Брезенхема построения окружности, но, получив координаты очередного пиксела, выведем не 8 точек, а 4 параллельных отрезка.
В настоящее время разработаны различные алгоритмы заполнения областей произвольной формы. Задачи заполнения областей можно разбить на 2 типа: заполнение многоугольников заданных своими вершинами и заполнение внутренности областей, заданных растровой разверткой границы.
Многоугольник – это фигура, ограниченная замкнутой ломаной без самопересечений. Он может быть задан последовательностью вершин А1,А2,...,Аn. Ребра определяются двумя соседними вершинами.
Ряд алгоритмов заполнения многоугольников основывается на том, что горизонтальная прямая, пересекающая ломаную, разбивает ее на чередующиеся интервалы, принадлежащие и не принадлежащие многоугольнику. Для каждого y найдем и отсортируем точки пересечения по возрастанию x. Сгруппируем их парами. Это будут отрезки, подлежащие закрашиванию (рис.6.1)
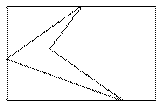
Рисунок 6.1
Улучшить этот алгоритм можно, используя список ребер, упорядоченный не по возрастанию ординат верхних концов ребер. В этот список не включаются горизонтальные ребра. Проверке подвергаются только те ребра, у которых наибольшая ордината больше ординаты сканируемой строки. Из списка исключаются ребра, расположенные под сканируемой строкой. Этот алгоритм позволяет разложить в растр произвольный многоугольник.
Для выпуклых многоугольников существуют более простые алгоритмы. Границы выпуклого многоугольника можно разбить на две части – левую и правую, исключив горизонтальные ребра. Каждая часть представляет собой упорядоченный список ребер.
Перемещаясь с помощью алгоритма Брезенхема одновременно по левой и правой границе, покрываем многоугольник горизонтальными отрезками, соединяя точки левой и правой границы с одинаковыми значениями y (рис.6.2).
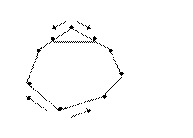
Рисунок 6.2
Этот алгоритм можно применить и для разложения в растр монотонного многоугольника. Многоугольник называется монотонным, если существует такое направление, что любая прямая в этом направлении пересекает многоугольник в двух точках.
Заполнение областей на растре
Задано разложение в растр границы области. Граница имеет цвет В. Задана точка на растре, называемая затравочной, принадлежащая области. Требуется закрасить область в цвет С. Областью называется множество пикселей, по которым существует путь по пикселям, цвет которых не равен цвету границы В. От пикселя к пикселю проходим по горизонтали или вертикали, т.е. будем рассматривать четырехсвязную область.
Простейшим алгоритмом заполнения является алгоритм ‘‘короед’’.
Procedure SimrleFill(x, y:integer;B,C:word);
begin
if (getpixel(x, y)<> B) and (getpixel(x, y)<> C) then
begin SimpleFill(x +1, y, B, C);
SimpleFill(x -1, y, B, C);
SimpleFill(x, y +1, B, C);
SimpleFill(x +1, y -1, B, C)
end;
end;
Реально используются алгоритмы построчного заполнения, основанные на том, что соседние пиксели в строке, скорее всего, одинаковы и меняются только там, где строка пересекается с ребром многоугольника. Это называется когерентностью растровых строк (строки сканирования Yi, Yi+1, Yi+2 на рис.6.3). При этом достаточно определить X-координаты пересечений строк сканирования с ребрами. Пары отсортированных точек пересечения задают интервалы заливки.
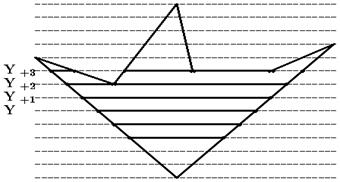
Рисунок 6.3 - Построчная закраска многоугольника
Кроме того, если какие-либо ребра пересекались i-й строкой, то они, скорее всего, будут пересекаться также и строкой i+1. (строки сканирования Yi и Yi+1 на рис. 6.3). Это называется когерентностью ребер. При переходе к новой строке легко вычислить новую X-координату точки пересечения ребра, используя X-координату старой точки пересечения и тангенс угла наклона ребра: Xi+1 = Xi + 1/k, где
тангенс угла наклона ребра - k = dy/dx, т. к. dy = 1, то 1/k = dx.
Смена же количества интервалов заливки происходит только тогда, когда в строке сканирования появляется вершина.
Варианты заданий
Выбор алгоритма зависит от r - остатка от деления номера варианта на 4.
1. Если r =0, реализовать алгоритм закраски для выпуклого и монотонного многоугольника.
2. Если r =1, реализовать алгоритм закраски произвольного многоугольника.
3. Если r =2, реализовать алгоритм заливки с затравкой выпуклой облас
|
|
|

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!