Масштаб показывает, во сколько раз каждая линия, нанесенная на карту или чертёж, меньше или больше её действительных размеров. Есть три вида масштаба: численный, именованный, графический. Масштабы на картах и планах могут быть представлены численно или графически.
Численный масштаб записывают в виде дроби, в числителе которой стоит единица, а в знаменателе — степень уменьшения проекции. Например, масштаб 1:5000 показывает, что 1 см на плане соответствует 5 000 см (50 м) на местности.
Более крупным является тот масштаб, у которого знаменатель меньше. Например, масштаб 1:1 000 крупнее, чем масштаб 1:25 000.
Графические масштабы подразделяются на линейные и поперечные. Линейный масштаб — это графический масштаб в виде масштабной линейки, разделённой на равные части. Поперечный масштаб — это графический масштаб в виде номограммы, построение которой основано на пропорциональности отрезков параллельных прямых, пересекающих стороны угла. Поперечный масштаб применяют для более точных измерений длин линий на планах. Поперечным масштабом пользуются следующим образом: откладывают на нижней линии поперечного масштаба замер длины таким образом, чтобы один конец (правый) был на целом делении ОМ, а левый заходил за 0. Если левая ножка попадает между десятыми делениями левого отрезка (от 0), то поднимаем обе ножки измерителя вверх, пока левая ножка не попадёт на пересечение к-либо трансвенсали и какой-либо горизонтальной линии. При этом правая ножка измерителя должна находиться на этой же горизонтальной линии. Наименьшая ЦД=0,2мм, а точность 0,1.
Точность масштаба — это отрезок горизонтального проложения линии, соответствующий 0,1 мм на плане. Значение 0,1 мм для определения точности масштаба принято из-за того, что это минимальный отрезок, который человек может различить невооруженным глазом. Например, для масштаба 1:10 000 точность масштаба будет равна 1 м. В этом масштабе 1 см на плане соответствует 10 000 см (100 м) на местности, 1 мм — 1 000 см (10 м), 0,1 мм — 100 см (1 м).
Масштабы изображений на чертежах должны выбираться из следующего ряда:
| Масштабы уменьшения
| 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1 000
|
| Натуральная величина
| 1:1
|
| Масштабы увеличения
| 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1
|
При проектировании генеральных планов крупных объектов допускается применять масштабы 1:2 000; 1:5 000; 1:10 000; 1:20 000; 1:25 000; 1:50 000.
В необходимых случаях допускается применять масштабы увеличения (100n):1, где n — целое число.
6. Топографические планы и карты. Разграфка и номенклатура.
Топографический план - это уменьшенная ортогональная проекция местности на горизонтальную плоскость.
Картой называется построенное в картографической проекции с учетом кривизны Земли, уменьшенное, обобщенное изображение Земли или отдельных ее частей.
Профиль представляет уменьшенное изображение вертикального разреза земной поверхности по заданному направлению. Профили используют для проектирования и строительства линейных инженерных сооружений.
Отличительные признаки плана и карты:
1) На планах изображается меньшая площадь, нет искажений длин линий и углов.
2) На планах не учитывается кривизна Земли.
3) На планах используют более крупные масштабы: 1:500, 1:1000, 1:2000, 1:5000;
на картах - 1:10000, 1:25000, 1:50000, 1:100000.
4) На планах нет параллелей и меридианов, а имеется только координатная сетка.
5) Различается номенклатура, т.е. система разграфки и обозначений отдельных листов карт и планов.
Большинство топографических карт создаётся в равноугольной поперечно-цилиндрической проекции Гаусса, при которой изображение земной поверхности на плоскости наносится по зонам, вытянутым от Северного полюса до Южного. Границами зон служат меридианы с долготой, кратной 6° (всего 60 зон - прим. от geoglobus.ru). В пределах каждой зоны поверхность проектируется на плоскость. Топографические карты создаются на большие территории и издаются отдельными листами, ограниченными рамками. Сторонами внутренних рамок служат линии параллелей и меридианов.
Система деления карты на отдельные листы называется разграфкой карты, а система обозначения (нумерации) листов — их номенклатурой.
Деление топографических карт на отдельные листы линиями меридианов и параллелей удобно тем, что рамки листов точно указывают положение на земном эллипсоиде участка местности, изображённого на данном листе, и его ориентировку относительно сторон горизонта.
Стандартные размеры листов карт различных масштабов указаны в таблице 1:
Таблица 1
| Масштаб карты
| Размеры листа
| На местности соответствует
|
| по широте (мин.)
| по долготе (мин.)
| длине боковой рамки листа, км
| площади листа, кв. км
|
| 1:25 000
| 5
| 7,5
| 9
| 75
|
| 1:50 000
| 10
| 15
| 18
| 300
|
| 1:100 000
| 20
| 30
| 37
| 1200
|
| 1:200 000
| 40
| 60
| 74
| 5000
|
| 1:500 000
| 120
| 180
| 220
| 44000
|
| 1:1 000 000
| 240
| 360
| 440
| 175000
|
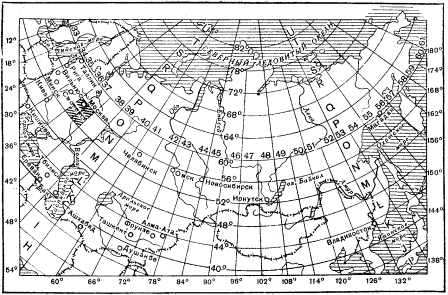
Схема разграфки карты масштаба 1:1 000 000 показана на рис.1.
Рис.1. Разграфка и номенклатура листов карты масштаба 1:1000000.
Принцип разграфки карт остальных масштабов (более крупных) показан на рис.2.
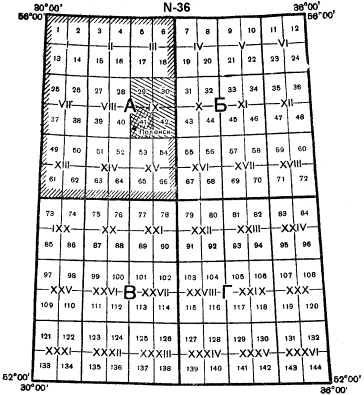
Рис.2. Расположение, порядок нумерации и обозначения листов карт масштабов 1:50 000 – 1:500 000 на листе миллионной карты.
Из таблицы 1 и этих рисунков видно, что листу миллионной карты соответствует целое число листов остальных масштабов, кратное четырём — 4 листа карты масштаба 1:500 000, 36 листов карты масштаба 1:200 000, 144 листа масштаба 1:100 000 и т.д.
В соответствии с этим установлена и номенклатура листов, единая для топографических карт всех масштабов. Номенклатура каждого листа указана над северной стороной его рамки.
В основу обозначения листов топографических карт любого масштаба положена номенклатура листов миллионной карты.
7. Рельеф земной поверхности и способы его изображения на планах и карте. Свойства горизонталей.
Для решения инженерных задач изображение рельефа должно обеспечивать: во-первых, быстрое определение с требуемой точностью высот точек местности, направления крутизны скатов и уклонов линий; во-вторых, наглядное отображение действительного ландшафта местности.
Рельеф местности на планах и картах изображают различными способами (штриховкой, пунктиром, цветной пластикой), но чаще всего с помощью горизонталей (изогипсов), числовых отметок и условных знаков.
Горизонталь на местности можно представить как след, образованный пересечением уровенной поверхности с физической поверхностью Земли. Например, если представить холм, окружённый неподвижной водой, то береговая линия воды и есть горизонталь (рис. 30). Лежащие на ней точки имеют одинаковую высоту.
Допустим, что высота уровня воды относительно уровенной поверхности 110 м (рис. 30). Предположим теперь, что уровень воды упал на 5 м и часть холма обнажилась. Кривая линия пересечения поверхностей воды и холма будет соответствовать горизонтали с высотой 105 м. Если последовательно снижать уровень воды по 5 м и проектировать кривые линии, образованные пересечением поверхности воды с земной поверхностью, на горизонтальную плоскость в уменьшенном виде, то получим изображение рельефа местности горизонталями на плоскости.
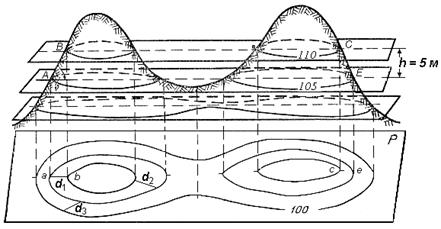 Таким образом, кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.
Таким образом, кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.
Рис. 30. Способ изображения рельефа горизонталями
При решении ряда инженерных задач необходимо знать свойства горизонталей:
1. Все точки местности, лежащие на горизонтали, имеют равные отметки.
2. Горизонтали не могут пересекаться на плане, поскольку они лежат на разных высотах. Исключения возможны в горных районах, когда горизонталями изображают нависший утес.
3. Горизонтали являются непрерывными линиями. Горизонтали, прерванные у рамки плана, замыкаются за пределами плана.
4. Разность высот смежных горизонталей называется высотой сечения рельефа и обозначается буквой h.
Высота сечения рельефа в пределах плана или карты строго постоянна. Её выбор зависит от характера рельефа, масштаба и назначения карты или плана. Для определения высоты сечения рельефа иногда пользуются формулой
h = 0,2 мм М,
где М – знаменатель масштаба.
Такая высота сечения рельефа называется нормальной.
5. Расстояние между соседними горизонталями на плане или карте называется заложением ската или склона. Заложение есть любое расстояние между соседними горизонталями (см. рис. 30), оно характеризует крутизну ската местности и обозначается d.
Вертикальный угол, образованный направлением ската с плоскостью горизонта и выраженный в угловой мере, называется углом наклона ската ν (рис. 31). Чем больше угол наклона, тем круче скат.
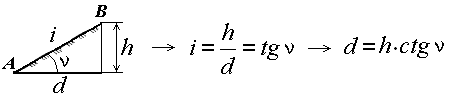
Рис. 31. Определение уклона и угла наклона ската
Другой характеристикой крутизны служит уклон i. Уклоном линии местности называют отношение превышения к горизонтальному проложению. Из формулы следует (рис. 31), что уклон безразмерная величина. Его выражают в сотых долях (%) или тысячных долях – промиллях (‰).
Если угол наклона ската до 45°, то он изображается горизонталями, если его крутизна более 45°, то рельеф обозначают специальными знаками.
Для изображения рельефа горизонталями выполняют топографическую съемку участка местности. По результатам съемки определяют координаты (две плановые и высоту) для характерных точек рельефа и наносят их на план. В зависимости от характера рельефа, масштаба и назначения плана выбирают высоту сечения рельефа h. Для инженерного проектирования обычно h = 1 м. Отметки горизонталей в этом случае будут кратны одному метру.
Положение горизонталей на плане или карте определяется с помощью интерполирования. На рис. 33 приведено построение горизонталей с отметками 51, 52, 53, 54, 55, 56, 57 м. Горизонтали кратные 5 или 10 м проводят на чертеже утолщенными и подписывают. Подписи наносят таким образом, чтобы верх цифр указывал сторону повышения рельефа. На рис. 33 подписана горизонталь с отметкой 55 м.
Там, где заложения больше, наносят штриховые линии (полугоризонтали). Иногда, чтобы сделать чертеж более наглядным, горизонтали сопровождают небольшими черточками, которые ставятся перпендикулярно горизонталям, по направлению ската (в сторону стока воды). Эти черточки называются бергштрихи.
Общие сведения из теории ошибок измерений. Основные понятия о точности измерений. Средняя квадратическая, предельная и относительные ошибки измерений.
Результаты измерений разделяют на равноточные и неравноточные. Под равноточными понимают однородные результаты, полученные в процессе измерений инструментами одного класса точности при одинаковых условиях, а неравноточные результаты измерений получают при несоблюдении условий равноточности.
Измерения различаются на необходимые и избыточные. Число измерений, требующихся для решения поставленной задачи, называют необходимыми. Например, при измерении длины линии, чтобы получить результат, необходимо выполнить одно измерение.
В геодезической практике всегда выполняют некоторое число избыточных измерений с тем, чтобы обеспечить контроль, повысить точность и получить сравнительные данные для оценки точности полученного результата.
В процессе измерений участвуют наблюдатель, приборы и условия внешней среды, которые постоянно меняются, что и приводит к неизбежным ошибкам измерений.
Ошибки измерений подразделяют на грубые, систематические и случайные.
Грубые ошибки возникают из-за промахов и просчетов, связанных с неисправностью приборов, невнимательностью наблюдателя, резким ухудшением внешних условий. Теория математической обработки не рассматривает измерения с грубыми ошибками, такие измерения либо отбрасываются, либо выполняются заново.
Систематические ошибки обычно имеют одну величину и знак и могут быть выявлены и учтены путем введения поправок в результате измерений. Например, при измерении длин линий лентой или рулеткой в зимнее время необходимо вводить в результаты измерений поправку за температуру.
Случайные ошибки неустранимы и неизбежны.
Для случайных ошибок установлены следующие свойства:
а) случайные ошибки для данных условий не могут превышать по абсолютной величине известного предела;
б) малые по абсолютной величине ошибки появляются чаще больших;
в) по знаку положительные ошибки появляются так же часто, как и равные им по величине отрицательные ошибки;
г) среднее арифметическое из случайных ошибок одной и той же величины неограниченно стремится к нулю с увеличением числа измерений. Это свойство можно записать так:
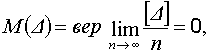 (1)
(1)
где ∆ – случайная ошибка; n – число измерений.
Если одна и та же величина равноточно измерена n раз, то за ее окончательное значение принимают среднее арифметическое, то есть:
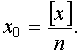
Для правильного использования результатов измерений необходимо знать, с какой точностью, т. е. с какой степенью близости к истинному значению измеряемой величины, они получены. Характеристикой точности отдельного измерения в теории ошибок служит предложенная Гауссом средняя квадратическая ошибка m, вычисляемая по формуле
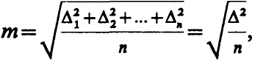 (5.2)
(5.2)
где п - число измерений данной величины.
Эта формула применима для случаев, когда известно истинное значение измеряемой величины. Такие случаи в практике встречаются редко. В то же время из измерений можно получить результат, наиболее близкий к истинному значению,- арифметическую средину. Для этого случая средняя квадратическая ошибка одного измерения подсчитывается по формуле Бесселя
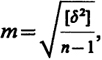 (5.3)
(5.3)
где δ - отклонения отдельных значений измеренной величины от арифметической средины, называемые вероятнейшими ошибками, причем [δ]=0.
Точность арифметической средины, естественно, будет выше точности отдельного измерения. Ее средняя квадратическая ошибка М определяется по формуле
М = m/√n(5.4)
где т - средняя квадратическая ошибка одного измерения, вычисляемая по формуле (5.2) или (5.3).
Часто в практике для контроля и повышения точности определяемую величину измеряют дважды - в прямом и обратном направлениях, например, длину линий, превышения между точками. Из двух полученных значений за окончательное принимается среднее из них. В этом случае средняя квадратическая ошибка одного измерения подсчитывается по формуле
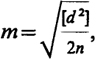 (5.5)
(5.5)
а средний результат из двух измерений - по формуле
39
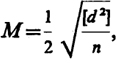 (5.6)
(5.6)
где d - разность двукратно измеренных величин, п - число разностей (двойных измерений).
В соответствии с первым свойством случайных ошибок для абсолютной величины случайной ошибки при данных условиях измерений существует допустимый предел, называемый предельной ошибкой. В строительных нормах предельная ошибка называется допускаемым отклонением.







 Таким образом, кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.
Таким образом, кривая линия, соединяющая все точки местности с равными отметками, называется горизонталью.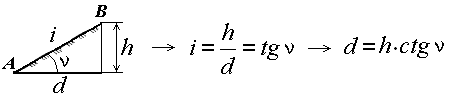
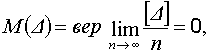 (1)
(1)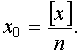
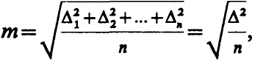 (5.2)
(5.2)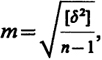 (5.3)
(5.3)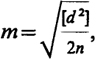 (5.5)
(5.5)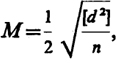 (5.6)
(5.6)

