Устойчивость и оптимизация
Как уже отмечалось, важным свойством или требованием,
предъявляемым к моделям, является требование их устойчивости.
Можно различить несколько аспектов понятия «устойчивость».
Устойчивость модели по отношению к изменениям ее параметров означает сохранение аппарата моделирования, основных связей между переменными, типов ограничений в некотором интервале ее параметров. Однако это требование является безусловным Традиционным свойством моделей сложных нелинейных динамических систем является наличие в пространстве параметров точек бифуркации (раздвоения), в которых одна траектория теряет устойчивость, и в ее окрестности появляется другая. Термин «бифуркация» в последние годы широко используется, в социологии и политологии, обозначая потерю устойчивости, многовариантность и непредсказуемость ближайшего будущего.ишь в отношении прагматических моделей.
Оптимизация заключается в том, чтобы среди множества объектов (возможных решений, сценариев, вариантов проектируемой системы) найти наилучшие в заданных условиях, при заданных ограничениях, то есть оптимальные альтернативы.
В этой фразе значение имеет каждое слово. Говоря «наилучшие», мы предполагаем, что у нас имеется критерий (или ряд критериев), способ (способы) сравнения вариантов. При этом важно учесть имеющиеся условия, ограничения, так как их изменение может привести к тому, что при одном и том же критерии (критериях) наилучшими окажутся другие варианты.
Понятие оптимальности получило строгое и точное представление в различных математических теориях, прочно вошло в практику проектирования и эксплуатации технических систем, сыграло
важную роль в формировании современных системных представлений, широко используется в административной и общественной практике, стало понятием, известным практически каждому человеку. Это и понятно: стремление к повышению эффективности труда, любой целенаправленной деятельности как бы нашло свое выражение, свою ясную и понятную форму в идее оптимизации.
Иногда оптимизация приводит к неустойчивости. Неустойчивость всегда присутствует в моделях, использующих аппарат линейного программирования: линейная целевая функция всегда достигает экстремума на границе симплекса, а значит, оптимальное
решение может стать недопустимым при малом изменении ситуации (например, минимизация затрат может привести к срыву плана выпуска продукции при малом увеличении расходов). Кроме того, модели, использующие аппарат линейного программирования, являются жесткими (оптимальное решение может сильно меняться при малом изменении коэффициентов целевой функции), однако развитость теоретического и алгоритмического аппаратов стимулирует их широкое использование в качестве «первого приближения».
Адекватность моделей
Устойчивость результатов моделирования по отношению к изменениям реальности достигается сочетанием свойств устойчивости и адекватности модели.
Адекватность тесно связана со свойством ингерентности и означает соответствие основных предположений, научного аппарата, методов, и, как следствие, результатов моделирования с одной стороны, моделируемой реальности, с другой – близким к ней моделям, теориям, парадигмам. Это, в частности, подразумевает корректное использование научного аппарата, методов компьютерного моделирования.
Более сложной является проблема адекватности базовых основ моделей, относящаяся к методологии моделирования. Отметим в этой связи, что бесконечномерный «каркас» (1), показывающий при «погружении» в него частных моделей одновременно их познавательный потенциал и ограничения, содержит в себе потенциал создания единой систематизации моделей и дает инструмент анализа их корректности. Действительно, корректная модель некоторого уровня сложности должна «содержать в себе» в агрегированном виде модели (или результаты моделирования) предшествующих уровней (при этом степень их детализации, конечно же, зависит от целей исследования). Для того чтобы лучше понять проблему адекватности, вернемся к рассмотрению процесса построения математической модели некоторой реальной системы и проанализируем
возможные ошибки моделирования. Первым шагом является выбор
того «языка», на котором формулируется модель, то есть того математического аппарата, который будет использоваться.
Например, не подлежит сомнению свойство динамичности организационных систем, однако использование традиционного при исследовании динамики аппарата дифференциальных уравнений в модели отдельно взятой организации почти всегда некорректно в силу значительной роли в ее динамике субъективных нерегулярных воздействий со стороны отдельных индивидов, а также в силу существенного влияния «истории», то есть той траектории, в результате которой данная организация оказалась в текущем своем состоянии.
Следующим этапом по уровню детализации является построение множества частных моделей, при переходе к которым вводятся те или иные предположения относительно параметров модели. Возникающие здесь ошибки могут быть вызваны неправильными представлениями о свойствах элементов моделируемой системы и их взаимодействии.
После задания структуры модели посредством выбора определенных значений параметров (в том числе – числовых) происходит переход к некоторой конкретной модели, которая считается аналогом моделируемого объекта. Источник возникающих на этом этапе «ошибок измерения» очевиден, хотя он имеет достаточно сложную природу и заслуживает отдельного обсуждения.
Оптимальное решение, полученное в рамках конкретной модели, является оптимальным в том смысле, что при его использовании поведение модели соответствует предъявляемым требованиям. Рассмотрим, насколько обоснованным является использование этого решения в реальной системе – моделируемом объекте.
Наблюдаемое поведение модели является с точки зрения субъекта, осуществляющего моделирование (например, полагающего, что модель адекватна), предполагаемым поведением реальной системы, которое в отсутствии ошибок моделирования будет оптимально в смысле выбранного критерия эффективности. Понятно, что в общем случае наблюдаемое поведение реальной системы и ее ожидаемое поведение могут различаться достаточно сильно. Следовательно, необходимо исследование адекватности модели, то есть – устойчивости поведения реальной системы относительно ошибок моделирования. Действительно, представим себе следующую ситуацию. Пусть построена модель и найдено оптимальное в ее рамках решение. А что будет, если параметры модели «немного» отличаются от параметров реальной системы? Получается, что задача выбора решалась «не для той» системы. Отрицать такую возможность, естественно, нельзя. Поэтому необходимо получить ответы на следующие вопросы:
- насколько оптимальное решение чувствительно к ошибкам описания модели, то есть, будут ли малые возмущения модели приводить к столь же малым изменениям оптимального решения (задача анализа устойчивости);
- будут ли решения, обладающие определенными свойствами в рамках модели (например, оптимальность, эффективность не ниже заданной и т.д.), обладать этими же свойствами и в реальной системе, и насколько широк класс реальных систем, в которых данное решение еще обладает этими свойствами (задача анализа адекватности). Качественно, основная идея, используемая на сегодняшний день в математическом моделировании, заключается в следующем. Применение оптимальных решений приводит к тому, что они, как правило, оказываются неоптимальными при малых вариациях параметров модели. Возможным путем преодоления этого недостатка является расширение множества «оптимальных» решений за счет включения в него так называемых приближенных решений (то есть, рациональных, «немного худших», чем оптимальные).Оказывается, что ослабление определения «оптимальность» позволяет, установив взаимосвязь между возможной неточностью описания
модели и величиной потерь в эффективности решения, гарантировать некоторый уровень эффективности множества решений в заданном классе реальных систем, то есть расширить область применимости решений за счет использования не самых эффективных, но «хороших». Иными словами, вместо рассмотрения фиксированной модели реальной системы, необходимо исследовать семейство моделей (т.е. действовать в рамках «мягкой» методологии). Приведенные качественные рассуждения свидетельствуют, что существует определенный дуализм между эффективностью решения и областью его применимости (областью его устойчивости и/или областью адекватности). В качестве отступления отметим, что этот эффект характерен не только для математических моделей, но и для различных отраслей науки. С точки зрения разделения наук на науки сильной и слабой версии, эту закономерность можно сформулировать следующим образом: более «слабые» науки вводят самые минимальные ограничивающие предположения (а то и не вводят их вовсе) и получают наиболее размытые результаты, «сильные» же науки наоборот – вводят множество ограничивающих предположений, используют специфические научные языки, но и получают более четкие и сильные (и, зачастую, более обоснованные) результаты, область применения которых весьма заужена (четко ограничена введенными предположениями).
Вводимые предположения (условия) ограничивают область применимости (адекватности) следующих из них результатов. Например, в области управления социально-экономическими системами математика (исследование операций, теория игр и т.д.) дает эффективные решения, но область их применимости (адекватности) существенно ограничена теми четкими предположениями, которые вводятся при построении соответствующих моделей. С другой стороны, общественные и гуманитарные науки, также исследующие управление социально-экономическими системами, почти не вводят предположений и предлагают «универсальные рецепты» (то есть область применимости, адекватности широка), но эффективность этих «рецептов» редко отличается от здравого смысла или обобщения позитивного практического опыта. Ведь без соответствующего исследования нельзя дать никаких гарантий, что управленческое решение, оказавшееся эффективным в одной ситуации, будет столь же эффективным в другой, пусть даже очень «близкой», ситуации. Поэтому можно условно расположить различные науки на плоскости «Обоснованность результатов» – «Область их применимости (адекватности)» и сформулировать (опять же условно, по аналогии с принципом неопределенности В. Гейзенберга) следующий «принцип неопределенности»: текущий уровень развития науки характеризуется определенными совместными ограничениями на «обоснованность» результатов и их общность.
9.Антагонистические игры с нулевой суммой. Понятие платежной матрицы, примеры ее построения.
Под игрой в математике понимается математическая модель конфликтной ситуации. При этом подразумевается, что каждый игрок имеет несколько вариантов поведения, а для всех комбинаций выборов игроков можно поставить в соответствие некоторый числовой выигрыш каждому игроку. Если сумма выигрышей всех игроков равна нулю, то игра называется игрой с нулевой суммой. Игра двух игроков с нулевой суммой называется антагонистической, т.к. цели игроков в ней прямо противоположны: выигрыш одного игрока происходит только за счет проигрыша другого.
В зависимости от количества стратегий игроков рассматривают конечные и бесконечные антагонистические игры. Конечную антагонистическую игру называют матричной игрой.
Определение антагонистической игры в нормальной форме: система, где  – непустые множества, а функция
– непустые множества, а функция  называется антагонистической игрой в нормальной форме. Элементы
называется антагонистической игрой в нормальной форме. Элементы  и
и 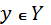 называются стратегиями игроков А и В соответственно, а функция К – функцией выигрыша игрока А. Выигрыш игрока В в ситуации (x, y) полагается равным
называются стратегиями игроков А и В соответственно, а функция К – функцией выигрыша игрока А. Выигрыш игрока В в ситуации (x, y) полагается равным 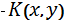 .
.
Для матричной игры функция выигрыша игрока А имеет вид платежной матрицы. Каждый элемент платежной матрицы aij является выигрышем игрока А (выигрыш игрока В равен – aij), определяемый использованием игроками стратегии А i и B j. Строки платежной матрицы соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В. Если у первого игрока m стратегий, а у второго игрока n стратегий, то платежная матрица имеет размер m x n:
|
| B1
| B2
| …
| B n
| | А1
| a 11
| a 12
| …
| a 1 n
| | А2
| a 21
| a 22
| …
| a 2 n
| | …
| …
|
|
|
| | A m
| am 1
| am 2
| …
| amn
|
| или
| 
|



 – непустые множества, а функция
– непустые множества, а функция  называется антагонистической игрой в нормальной форме. Элементы
называется антагонистической игрой в нормальной форме. Элементы  и
и 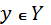 называются стратегиями игроков А и В соответственно, а функция К – функцией выигрыша игрока А. Выигрыш игрока В в ситуации (x, y) полагается равным
называются стратегиями игроков А и В соответственно, а функция К – функцией выигрыша игрока А. Выигрыш игрока В в ситуации (x, y) полагается равным 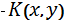 .
.


