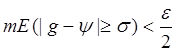Аk = E(|f|>k), Q = E(|f| = + ¥).
По условию, mQ = 0. Ввиду очевидных соотношений
А1 É А2 É А3 É …, 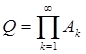
будет (теорема 12) при k®¥
mAk®mQ = 0.
Значит, найдется такое k0, что mAk0<e.
Определим на множестве E функцию g(x), полагая
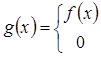
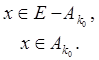

Эта функция измерима и, кроме того, ограничена, поскольку g (x)ê k0. Наконец, E(f ¹ g) = Ako, что и доказывает теорему.
Доказанная теорема означает, что всякая измеримая и почти везде конечная функция становится ограниченной, если пренебречь множеством сколь угодно малой меры.
Определение. Пусть функция F(x) задана на множестве E и x0ÎE, причем F(x0) ¹±¥. Говорят, что функция F(x) непрерывна в точке х0 в двух случаях: 1) если х0 есть изолированная точка E; 2) если х0Î E¢ и соотношения xn®x0, xnÎE влекут соотношение
f(xn) ®f(x0).
Если f(x) непрерывна в каждой точке множества E, то говорят, что она непрерывна на этом множестве.
Лемма 1. Пусть множества F 1, F 2, …, Fn замкнуты и попарно не пересекаются. Если функция j (х), заданная на множестве
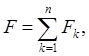
постоянна на каждом из множеств Fk , то она непрерывна на множестве F.
Д о к а з а т е л ь с т в о. Пусть x0ÎF’ и xi®x0, xiÎF.
В силу замкнутости множества F точка x0 принадлежит этому множеству и, стало быть, найдется такое m, что x0ÎFm.
Но множества Fk попарно не пересекаются. Значит, если k¹m, то х0  Fk и, в силу замкнутости множества Fk, точка x0 не является и предельной точкой этого множества.
Fk и, в силу замкнутости множества Fk, точка x0 не является и предельной точкой этого множества.
Отсюда следует, что в последовательности {xi} может быть только конечное число точек, принадлежащих множеству Fk при k¹m. Отметим все члены последовательности, которые входят в одно из множеств F1, …, Fm-1, Fm+1, …, Fn, и пусть xi0, последний из них. Тогда при i > i0 необходимо будет x1ÎFm, т.е. при i > i0 оказывается j (xi) = j (x0), а это доказывает лемму.
Лемма 2. Пусть F есть замкнутое множество, содержащееся в сегменте [ a, b ]. Если функция j (x) задана и непрерывна на множестве F, то можно определить на [ a, b ] функцию y (x) со следующими свойствами
1) y (x) непрерывна;
2) если x Î F, то y (x)= j (x);
3) max | y (x)| = max | j (x)|.
Д о к а з а т е л ь с т в о. Обозначим через [a, b] наименьший сегмент, содержащий множество F. Если бы требуемая функция y(x) была уже построена на сегменте [a, b], то достаточно было бы дополнить ее определение, полагая
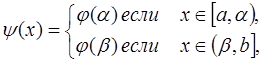
чтобы получить требуемую функцию уже на всем сегменте [a, b].
Поэтому, не ограничивая общности, можно считать что [a, b] и есть наименьший сегмент, содержащий множество F.
Если F = [a, b], то теорема тривиальна. Будем считать, что F ¹ [a, b]. Тогда множество [a, b] – F состоит из конечного или счетного множества взаимно не налегающих интервалов, концы которых принадлежат F (дополнительных интервалов множества F).
Зададим функцию y(x), полагая ее равной j(x) в точках множества F и линейной на всех дополнительных интервалах.
Убедимся в непрерывности этой функции. Непрерывность ее в каждой точке множества [a, b] – F очевидна.
Пусть х0 есть точка множества F. Мы покажем, что функция y(x) непрерывна в этой точке слева (непрерывность справа устанавливается совершенно аналогично).
Если точка х0 служит правым концом какого-нибудь дополнительного интервала, то непрерывность функции y(x) в этой точке слева очевидна.
Пусть же x0 не является правым концом никакого дополнительного интервала и пусть x1< x2< x3<… последовательность точек, стремящихся к x0.
Если xnÎF (n = 1, 2, 3, …) то, используя непрерывность на множестве F функции j(x), имеем y(xn) = j(xn) ® j(x0) =y(x0). Поэтому можно считать, что хn 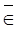 F (n = 1, 2, 3, …).
F (n = 1, 2, 3, …).
В таком случае точка x1 попадает в какой-то дополнительный интервал (l1, m1), причем m1<х0. Продолжая это рассуждение, мы приходим к последовательности (l1, m1), (l2, m2), (l3, m3), … дополнительных интервалов, расположенных в порядке номеров слева направо и таких, что
XkÎ(l1, m1) (k = ni-1+1, …, ni).
Соотношение xni<mi<x0 показывает, что mi, а из того, что mi-1£li< x0, ясно, что и li ®x0.
Но li и mi входят в F, так что
lim y(li) = lim y(mi) = y(x0).
Ввиду того, что значения линейной функции в каком-нибудь интервале лежат между ее значениями на концах этого интервала, ясно, что и limy(xn)=y(x0).
Итак, непрерывность функции y(x) доказана.
Из самого ее построения видно, что она совпадает с j(x) на множестве F.
Наконец по известной теореме Вейерштрасса, среди значений непрерывной на сегменте функции |y(x)| есть наибольшее – max |y(x)|. Легко видеть, что этот максимум достигается именно в точке, принадлежащей множеству F, ибо на дополнительных интервалах функция y(x) линейна. Поэтому max |y(x)| = max |j(x)|.
Лемма доказана полностью.
Теорема 2 (Э. Борель). Пусть на сегменте [ a, b] задана измеримая и почти везде конечная функция f(x). Каковы бы ни были числа s >0 и e >0 существует непрерывная на [ a, b] функция y(x), для которой
mE(| f- y| ³ s) < e
Если при этом | f(x)| £ K, то можно и y(x) выбрать так, что | y(x)| £ K.
Д о к а з а т е л ь с т в о. Предположим сначала, что |f(x)| £ K, т.е. что функция f(x) ограничена.
Фиксируя произвольные s >0 и e >0, найдем столь большое натуральное m, что K/m<s, и построим множества
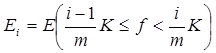 (i = 1 – m, 2 – m, …, m – 1)
(i = 1 – m, 2 – m, …, m – 1)
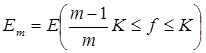
Эти множества измеримы, попарно не пересекаются и
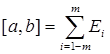
Построим для каждого i замкнутое множество Fi Ì Ei с мерой 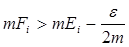 и положим
и положим 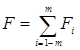 .
.
Ясно, что 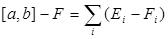 , откуда m[a, b] – mF<e.
, откуда m[a, b] – mF<e.
Зададим теперь на множестве F функцию j(x), полагая
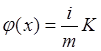 при xÎFi (i = 1 – m, …, m).
при xÎFi (i = 1 – m, …, m).
В силу леммы 1 эта функция непрерывна на множестве F, |j(x)| £ K и, наконец, при xÎF будет |f(x) - j(x)| < s.
Остается применить лемму 2. Это приводит к непрерывной функции y(x), совпадающей на множестве F с функцией j(x), причем |j(x)|³K. Поскольку E (| f - y | ³ s) Ì [a, b] – F, ясно, что функция y(x) требуемая.
Итак, для ограниченной функции теорема доказана.
Допустим теперь, что f (x) не ограничена. Тогда, пользуясь теоремой 1, можно построить такую ограниченную функцию g(x), что mE (f ¹ g) < e/2.
Применяя уже доказанную часть теоремы к функции g(x), мы найдем такую непрерывную функцию y(x), что
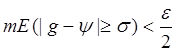
Но легко видеть, что
E (|f-y| ³ s) Ì E (f ¹ g) + E (|g-y| ³ s),
Так что функция y(x) решает задачу.
Следствие. Для всякой измеримой и почти везде конечной функции f (x), заданной на сегменте [ a, b ], существует последовательность непрерывных функций y n (x), сходящаяся по мере к функции f (x).


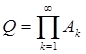
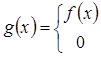
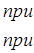
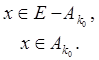

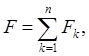
 Fk и, в силу замкнутости множества Fk, точка x0 не является и предельной точкой этого множества.
Fk и, в силу замкнутости множества Fk, точка x0 не является и предельной точкой этого множества.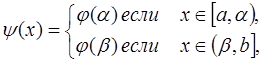
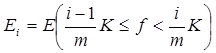 (i = 1 – m, 2 – m, …, m – 1)
(i = 1 – m, 2 – m, …, m – 1)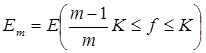
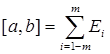
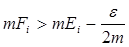 и положим
и положим 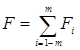 .
.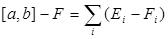 , откуда m[a, b] – mF<e.
, откуда m[a, b] – mF<e.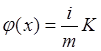 при xÎFi (i = 1 – m, …, m).
при xÎFi (i = 1 – m, …, m).