Однородная система уравнений
 (1)
(1)
есть частный случай системы (10.1). Легко видеть, что система (1) всегда имеет нулевое решение  , и поэтому она совместна. Нулевое решение является единственным тогда, когда ранг матрицы системы равен количеству неизвестных n. В частности, это справедливо для невырожденной системы n уравнений с n неизвестными. Если ранг матрицы А системы (1) меньше n, то однородная система (1) будетиметь ненулевые решения. Например, однородная система n линейных уравнений с n неизвестными имеет ненулевые решения в том случае, если она вырождена.
, и поэтому она совместна. Нулевое решение является единственным тогда, когда ранг матрицы системы равен количеству неизвестных n. В частности, это справедливо для невырожденной системы n уравнений с n неизвестными. Если ранг матрицы А системы (1) меньше n, то однородная система (1) будетиметь ненулевые решения. Например, однородная система n линейных уравнений с n неизвестными имеет ненулевые решения в том случае, если она вырождена.
18. Понятие вектора. По аналогии со школьным курсом геометрии дадим геометрическое толкование вектора, как направленного отрезка (п. 1.10) на плоскости или в пространстве.
Связанным вектором  с началом в точке А и концом в точке В называют направленный отрезок АВ, в котором точка А является началом, а точка В – концом. Начало вектора называют еще точкой его приложения.
с началом в точке А и концом в точке В называют направленный отрезок АВ, в котором точка А является началом, а точка В – концом. Начало вектора называют еще точкой его приложения.
Векторы также обозначают одной буквой с чертой над ней, например,  . Направление вектора на рисунке указывают стрелкой (рис. 1).
. Направление вектора на рисунке указывают стрелкой (рис. 1).

Если для направленного отрезка
АВ фиксируются только длина и направление (при произвольности его положения на плоскости и в пространстве), то он называется
свободным вектором.
Длина  отрезка АВ называется также длиной
отрезка АВ называется также длиной  вектора
вектора  . Вектор нулевой длины называется нулевым и обозначается
. Вектор нулевой длины называется нулевым и обозначается  или просто 0.
или просто 0.
Векторы  и
и  называются коллинеарными (параллельными), если они лежат на одной прямой или на параллельных прямых, при этом пишут
называются коллинеарными (параллельными), если они лежат на одной прямой или на параллельных прямых, при этом пишут 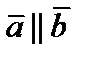 .
.
Векторы  и
и  называются одинаково направленными, если полупрямые
называются одинаково направленными, если полупрямые  и
и  одинаково направлены, и противоположно направленными, если эти полупрямые противоположно направлены.
одинаково направлены, и противоположно направленными, если эти полупрямые противоположно направлены.
Отметим, что коллинеарные векторы могут быть направлены одинаково (сонаправлены, см. рис. 2б)) или противоположно направлены (см. рис. 2а)).
Векторы  и
и  называются равными (
называются равными (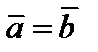 ), если выполнены два условия:
), если выполнены два условия:
а)  ;
;
б)  и
и  одинаково направлены.
одинаково направлены.

Векторы, имеющие противоположные направления и равные длины, называются
противоположными. Вектор, противоположный вектору

, обозначается

. На рис. 2а) изображены противоположные, а на рис. 2б) – равные векторы

и

.
Из определения равенства векторов следует, что каков бы ни был вектор  и точка О, всегда можно построить единственный вектор
и точка О, всегда можно построить единственный вектор  с началом в точке О, равный вектору
с началом в точке О, равный вектору  , или, как говорят, отнести начало вектора
, или, как говорят, отнести начало вектора  к точке О
к точке О
(см. рис. 3). Такие векторы в аналитической геометрии называют свободными: их можно отнести к общему началу. Проекция вектора на ось. Пусть в пространстве заданы ось  и некоторый вектор
и некоторый вектор  . Проведем через точки А и В плоскости, перпендикулярные данной оси
. Проведем через точки А и В плоскости, перпендикулярные данной оси  и обозначим через
и обозначим через  и
и 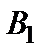 точки пересечения этих плоскостей с осью
точки пересечения этих плоскостей с осью  (рис.4). В общем случае векторырасположены на скрещивающихся прямых. Для наглядности изображений далее, как правило, будут рассматриваться рисунки на плоскости.
(рис.4). В общем случае векторырасположены на скрещивающихся прямых. Для наглядности изображений далее, как правило, будут рассматриваться рисунки на плоскости.

Рис. 4 Рис. 5а) Рис. 5б)
Проекцией вектора  на ось
на ось  называется величина
называется величина 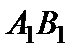 на оси
на оси  , которая обозначается
, которая обозначается  .
.
Согласно пункту 1.10, имеем:  , если направление
, если направление  совпадает с направлением оси
совпадает с направлением оси  ;
; 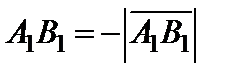 , если направление
, если направление  противоположно направлению оси
противоположно направлению оси  .
.
Покажем, что имеет место равенство
 , (1)
, (1)
где  – угол между вектором
– угол между вектором  и положительным направлением оси
и положительным направлением оси  .
.
19. Координаты вектора. Пусть в пространстве задана декартова система координат 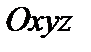 и произвольный вектор
и произвольный вектор  . Обозначим:
. Обозначим: 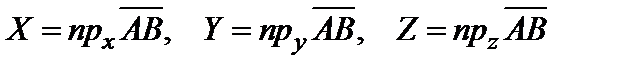 и назовем эти числа
и назовем эти числа 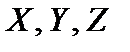 (проекции вектора
(проекции вектора  на оси координат) координатами вектора
на оси координат) координатами вектора  . Будем писать
. Будем писать  (символ
(символ  для краткости, как правило, далее опускаем).
для краткости, как правило, далее опускаем).
Докажем, что для любых точек  и
и  координаты вектора
координаты вектора  определяются формулами:
определяются формулами:
 . (2)
. (2)
Длина вектора. Рассмотрим произвольный вектор  считая, что его начало совпадает с началом координат
считая, что его начало совпадает с началом координат  . Пусть вектор
. Пусть вектор  не лежит ни в одной координатной плоскости.
не лежит ни в одной координатной плоскости.

Через точку
А проведем плоскости, которые перпендикулярны осям координат и вместе с координатными плоскостями образуют прямоугольный параллелепипед, диагональю которого будет отрезок
ОА (рис. 7).
Известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений, т.е.
 .
.
Но 
Тогда имеем  или
или
 . (3)
. (3)
Формула (3) выражает длину вектора через его координаты и справедлива и в том случае, если вектор  будет лежать в какой-либо координатной плоскости (тогда в (3) одна из координат будет равна нулю).
будет лежать в какой-либо координатной плоскости (тогда в (3) одна из координат будет равна нулю).
Пример 1. Даны две точки  и
и  Найти расстояние между ними.
Найти расстояние между ними.
Решение. Определим расстояние между точками А и В, как длину вектора 
 . □ (4)
. □ (4)
Направляющие косинусы вектора. Обозначим через  углы между вектором
углы между вектором  и осями координат (рис.7). Из формул (1) и (3) получаем:
и осями координат (рис.7). Из формул (1) и (3) получаем:
 (5)
(5)
Числа  называются направляющими косинусамивектора
называются направляющими косинусамивектора  .
.
Возводя в квадрат каждое из равенств (5) и складывая полученные результаты, получим
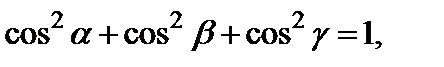 (6)
(6)
т.е. сумма квадратов направляющих косинусов любого вектора равна единице.
20.Линейными операциями над векторами называют операции сложения векторов и умножения вектора на число.
Пусть даны два вектора  и
и  . Суммой
. Суммой  называется вектор, который имеет началом начало вектора
называется вектор, который имеет началом начало вектора  и концом – конец вектора
и концом – конец вектора  при условии, что начало вектора
при условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора  (или диагональ параллелограмма, построенного на векторах
(или диагональ параллелограмма, построенного на векторах  и
и  ).
).
Отсюда следует, что сумму неколлинеарных векторов  и
и  можно найти по правилу треугольника (рис. 8а)) или параллелограмма (рис. 8б)).
можно найти по правилу треугольника (рис. 8а)) или параллелограмма (рис. 8б)).

Рис. 8а) Рис. 8б)
По определению суммы двух векторов можно найти сумму любого числа заданных векторов. В частности, пусть заданы три вектора  и
и  . Сложив
. Сложив  и
и  , получим вектор
, получим вектор  Прибавив к нему вектор
Прибавив к нему вектор  , получим вектор
, получим вектор 
Разностью  векторов
векторов  и
и  называется вектор
называется вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор  .
.
Пусть даны вектор  и число
и число 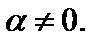 Произведением
Произведением  называют вектор, который коллинеарен вектору
называют вектор, который коллинеарен вектору  , имеет длину, равную
, имеет длину, равную  , и направление такое же, как и вектор
, и направление такое же, как и вектор  , если
, если  , и противоположное, если
, и противоположное, если  (рис. 9). Если среди сомножителей
(рис. 9). Если среди сомножителей  есть 0, то под произведением
есть 0, то под произведением  понимается нулевой вектор.
понимается нулевой вектор.
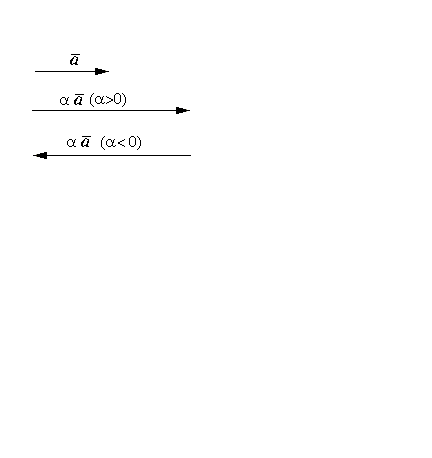
Геометрический смысл операции умножения вектора на число следующий: если

, то при умножении вектора

на число

вектор

«растягивается» в

раз, а если
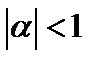
– «сжимается» в

раз. На рис. 9 изображен случай

.
Утверждение 1. Если векторы  и
и  коллинеарны и
коллинеарны и  , то существует единственное число
, то существует единственное число  , что
, что  .
.



 (1)
(1) , и поэтому она совместна. Нулевое решение является единственным тогда, когда ранг матрицы системы равен количеству неизвестных n. В частности, это справедливо для невырожденной системы n уравнений с n неизвестными. Если ранг матрицы А системы (1) меньше n, то однородная система (1) будетиметь ненулевые решения. Например, однородная система n линейных уравнений с n неизвестными имеет ненулевые решения в том случае, если она вырождена.
, и поэтому она совместна. Нулевое решение является единственным тогда, когда ранг матрицы системы равен количеству неизвестных n. В частности, это справедливо для невырожденной системы n уравнений с n неизвестными. Если ранг матрицы А системы (1) меньше n, то однородная система (1) будетиметь ненулевые решения. Например, однородная система n линейных уравнений с n неизвестными имеет ненулевые решения в том случае, если она вырождена. с началом в точке А и концом в точке В называют направленный отрезок АВ, в котором точка А является началом, а точка В – концом. Начало вектора называют еще точкой его приложения.
с началом в точке А и концом в точке В называют направленный отрезок АВ, в котором точка А является началом, а точка В – концом. Начало вектора называют еще точкой его приложения. . Направление вектора на рисунке указывают стрелкой (рис. 1).
. Направление вектора на рисунке указывают стрелкой (рис. 1).
 отрезка АВ называется также длиной
отрезка АВ называется также длиной  вектора
вектора  или просто 0.
или просто 0. называются коллинеарными (параллельными), если они лежат на одной прямой или на параллельных прямых, при этом пишут
называются коллинеарными (параллельными), если они лежат на одной прямой или на параллельных прямых, при этом пишут 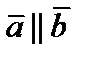 .
. и
и  называются одинаково направленными, если полупрямые
называются одинаково направленными, если полупрямые  и
и  одинаково направлены, и противоположно направленными, если эти полупрямые противоположно направлены.
одинаково направлены, и противоположно направленными, если эти полупрямые противоположно направлены.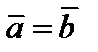 ), если выполнены два условия:
), если выполнены два условия: ;
;
 . На рис. 2а) изображены противоположные, а на рис. 2б) – равные векторы
. На рис. 2а) изображены противоположные, а на рис. 2б) – равные векторы  с началом в точке О, равный вектору
с началом в точке О, равный вектору  и некоторый вектор
и некоторый вектор  и
и 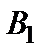 точки пересечения этих плоскостей с осью
точки пересечения этих плоскостей с осью 
 называется величина
называется величина 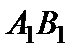 на оси
на оси  .
. , если направление
, если направление  совпадает с направлением оси
совпадает с направлением оси 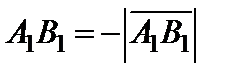 , если направление
, если направление  , (1)
, (1) – угол между вектором
– угол между вектором 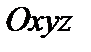 и произвольный вектор
и произвольный вектор  . Обозначим:
. Обозначим: 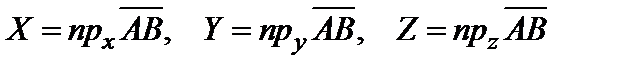 и назовем эти числа
и назовем эти числа 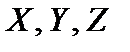 (проекции вектора
(проекции вектора  (символ
(символ  для краткости, как правило, далее опускаем).
для краткости, как правило, далее опускаем). и
и  координаты вектора
координаты вектора  . (2)
. (2) считая, что его начало совпадает с началом координат
считая, что его начало совпадает с началом координат  . Пусть вектор
. Пусть вектор  не лежит ни в одной координатной плоскости.
не лежит ни в одной координатной плоскости.
 .
.
 или
или . (3)
. (3) и
и  Найти расстояние между ними.
Найти расстояние между ними.
 . □ (4)
. □ (4) углы между вектором
углы между вектором  (5)
(5) называются направляющими косинусамивектора
называются направляющими косинусамивектора 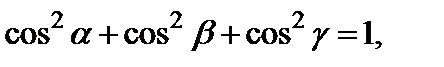 (6)
(6) . Суммой
. Суммой  называется вектор, который имеет началом начало вектора
называется вектор, который имеет началом начало вектора 
 и
и  . Сложив
. Сложив  Прибавив к нему вектор
Прибавив к нему вектор 
 векторов
векторов  и число
и число 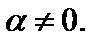 Произведением
Произведением  называют вектор, который коллинеарен вектору
называют вектор, который коллинеарен вектору  , и направление такое же, как и вектор
, и направление такое же, как и вектор  , и противоположное, если
, и противоположное, если  (рис. 9). Если среди сомножителей
(рис. 9). Если среди сомножителей  есть 0, то под произведением
есть 0, то под произведением  понимается нулевой вектор.
понимается нулевой вектор.
 , то при умножении вектора
, то при умножении вектора  вектор
вектор 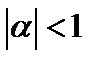 – «сжимается» в
– «сжимается» в  раз. На рис. 9 изображен случай
раз. На рис. 9 изображен случай  , то существует единственное число
, то существует единственное число  .
.


