S i = h f (x i), i = 1,2,..., n;  . .
| (6.3)
|
и в методе средних прямоугольников
S i = h  ), i = 0,1,2,..., n -1; ), i = 0,1,2,..., n -1;  , ,
| (6.4)
|
где  , i = 0,1,2,..., n -1.
, i = 0,1,2,..., n -1.
Приведенные формулы для S являются вычислительными формулами методов прямоугольников.
На рис.6.5. приведена блок-схема вычисления определенного интеграла методом средних прямоугольников.

Рис.6.5. Алгоритм метода средних прямоугольников
Алгоритмы для методов левых и правых прямоугольников отличаются от изображенного на рис.6.5 лишь одним блоком (он выделен жирной линией). Для метода левых прямоугольников здесь должно стоять X=A, для метода правых прямоугольников должно быть X=A+h.
Оценим точность этих методов. В методе средних прямоугольников для каждого интервала разбиения получаем c учетом выражения для S i в (6.4):
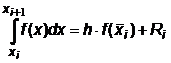 . .
| (6.5)
|
Для оценки R i разложим функцию f (x) в ряд Тейлора около средней точки 
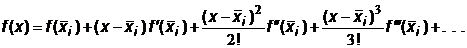
| (6.6)
|
В малой окрестности точки  этот ряд с высокой точностью представляет функцию f (x) при небольшом количестве членов разложения. Поэтому, подставляя под знак интеграла вместо f (x) ее тейлоровское разложение (6.6) и интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью. T.е. точное значение интеграла на интервале [ x i, x i+1] равно:
этот ряд с высокой точностью представляет функцию f (x) при небольшом количестве членов разложения. Поэтому, подставляя под знак интеграла вместо f (x) ее тейлоровское разложение (6.6) и интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью. T.е. точное значение интеграла на интервале [ x i, x i+1] равно:

Подставим пределы интегрирования:

или, так как  :
:

Все члены полученного при интегрировании ряда, имеющие (x - x i) в четной степени, обращаются в нуль. Поэтому получаем:

| (6.7)
|
Сравнивая (6.5) и (6.7), можно записать выражение для погрешности R i:

При малой величине шага интегрирования h основной вклад в значение R i дает первое слагаемое, которое называется главным членом погрешности вычисления интеграла на интервале [ x i, x i+1] и обозначается R 0i:
 . .
| (6.8)
|
Главный член полной погрешности для интеграла на всем промежутке [ a,b ] определится как сумма:
 . .
| (6.9)
|
Здесь использован тот же метод средних прямоугольников, но для функции  .
.
Степень шага h, которой пропорциональна величина R 0, называется порядком метода интегрирования. Как видно из (6.9 ), метод средних прямоугольников имеет второй порядок.
Аналогично проведем оценку метода левых прямоугольников. Разложим подынтегральную функцию в ряд Тейлора в окрестности точки x = x i:

Интегрируя это разложение почленно на интервале [ x i, x i+1] получаем

Здесь первое слагаемое есть приближенное значение интеграла, вычисленное по методу левых прямоугольников (см. формулу (6.2)), а второе слагаемое является главным членом погрешности:
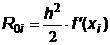 . .
|
(6.10)
|
Тогда на всем промежутке интегрирования [ a,b ] главный член погрешности R 0 получается суммированием частичных погрешностей R 0i:
 , ,
|
(6.11)
|
т.е. метод левых прямоугольников имеет первый порядок. Метод правых прямоугольников также имеет первый порядок.
Сравнение (6.9) и (6.11) показывает, что метод средних прямоугольников имеет меньшую погрешность по сравнению с методом левых или правых прямоугольников и за счет коэффициента в знаменателе (24 > 2), и за счет интеграла от производной, т.к. для большинства функций выполняется неравенство
 .
.
Следовательно, использование метода средних прямоугольников является предпочтительным, но использовать его удается не всегда. Если значения f (x) определяются из эксперимента в дискретном наборе узлов, то метод средних прямоугольников напрямую применить нельзя из-за отсутствия значений f (x) в срединных точках. В этой ситуации приходится применять либо какие-нибудь средства интерполяции, что приводит к дополнительным расходам машинного времени и памяти, либо другие методы численного интегрирования.
Метод трапеций
В этом методе подынтегральная функция f (x) на интервале [ x i, x i+1] заменяется полиномом первой степени, т.е. наклонной прямой линией. Обычно эта прямая проводится через значения f (x) на границах интервала (рис.6.6). В этом случае приближенное значение частичного интеграла определяется площадью трапеции:
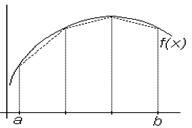 Рис.6.6. Геометрическая
интерпретация метода
трапеций
Рис.6.6. Геометрическая
интерпретация метода
трапеций
| 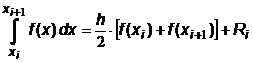 ,
т.е. ,
т.е. 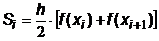 ,
а численное значение интеграла на всем [ a,b ] ,
а численное значение интеграла на всем [ a,b ]
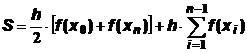 .
Это вычислительная формула метода трапеций. .
Это вычислительная формула метода трапеций.
|
(6.12)
(6.13)
|
Блок-схему алгоритма метода трапеций предлагается студентам разработать самим.
Оценим погрешность R i. Для этого разложим функцию f (x) в ряд Тейлора около точки x i:

| (6.14)
|
Тогда

| (6.15)
|
С помощью разложения (6.14) вычислим подынтегральную функцию в точке x i+ h:

откуда
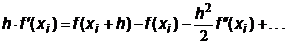
| (6.16)
|
Подставляя произведение (6.16) в выражение (6.15), получим
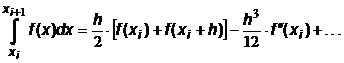
| (6.17)
|
Сравнивая (6.12) и (6.17), получаем выражение для главного члена погрешности частичного интеграла
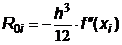 .
.
Тогда главный член полной погрешности метода трапеций имеет вид
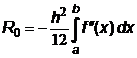 , ,
|
(6.18)
|
т.е. метод трапеций имеет также второй порядок, но его погрешность в два раза больше, чем в методе средних прямоугольников, поэтому, если подынтегральная функция задана аналитически, то предпочтительнее из методов второго порядка использовать метод средних прямоугольников.



 .
.
 ), i = 0,1,2,..., n -1;
), i = 0,1,2,..., n -1;  ,
,
 , i = 0,1,2,..., n -1.
, i = 0,1,2,..., n -1.
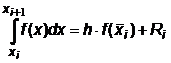 .
.

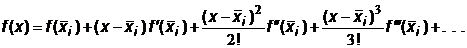
 этот ряд с высокой точностью представляет функцию f (x) при небольшом количестве членов разложения. Поэтому, подставляя под знак интеграла вместо f (x) ее тейлоровское разложение (6.6) и интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью. T.е. точное значение интеграла на интервале [ x i, x i+1] равно:
этот ряд с высокой точностью представляет функцию f (x) при небольшом количестве членов разложения. Поэтому, подставляя под знак интеграла вместо f (x) ее тейлоровское разложение (6.6) и интегрируя его почленно, можно вычислить интеграл с любой наперед заданной точностью. T.е. точное значение интеграла на интервале [ x i, x i+1] равно:

 :
:


 .
.
 .
.
 .
.

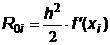 .
.
 ,
,
 .
. Рис.6.6. Геометрическая
интерпретация метода
трапеций
Рис.6.6. Геометрическая
интерпретация метода
трапеций
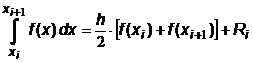 ,
т.е.
,
т.е. 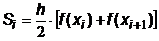 ,
а численное значение интеграла на всем [ a,b ]
,
а численное значение интеграла на всем [ a,b ]
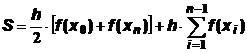 .
Это вычислительная формула метода трапеций.
.
Это вычислительная формула метода трапеций.



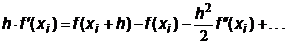
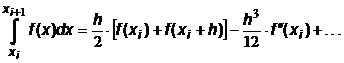
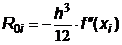 .
.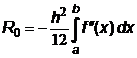 ,
,



