3.3.1. Адекватность. Оценка качества регрессионных моделей с бинарной зависимой переменной осуществляется практически по той же схеме, что и качество обычной линейной регрессии: определяется пригодность модели в целом, затем определяется статистическая значимость каждого коэффициента модели и, наконец, проверяются гипотезы (если они имеют место), относительно ограничений, которым могут удовлетворять отдельные группы параметров.
Пригодность модели в целом (адекватность) определяется с помощью двух показателей. В качестве первого рассмотрим предложенный Макфадденом (McFadden) индекс отношения правдоподобия
 , (3.53)
, (3.53)
где  – максимальное значение логарифмической функции правдоподобия, достигаемое в точке, координаты которой равны оценкам параметров модели
– максимальное значение логарифмической функции правдоподобия, достигаемое в точке, координаты которой равны оценкам параметров модели  , а
, а 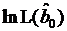 – значение логарифмической функции правдоподобия, вычисленное в предположении, что
– значение логарифмической функции правдоподобия, вычисленное в предположении, что  . (Во многих пакетах предусмотрен расчет этих значений функции правдоподобия).
. (Во многих пакетах предусмотрен расчет этих значений функции правдоподобия).
Интуиция подсказывает, что значения такого критерия должны быть заключены между 0 и 1. Действительно, в случае, когда все коэффициенты кроме  , равны нулю, индекс отношения правдоподобия тоже равен нулю. Если же модель оказалась такой, что ее расчетные значения
, равны нулю, индекс отношения правдоподобия тоже равен нулю. Если же модель оказалась такой, что ее расчетные значения 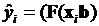 в точности совпадают с наблюдаемыми значениями
в точности совпадают с наблюдаемыми значениями 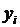 , т.е. имеют место только случаи или
, т.е. имеют место только случаи или 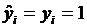 , или
, или  , то индекс
, то индекс  . О такой модели принято говорить, что она совершенно согласована. В остальных случаях значение
. О такой модели принято говорить, что она совершенно согласована. В остальных случаях значение  заключено между 0 и 1, причем, чем больше совпадений между расчетными и фактическими значениями, тем ближе значение индекса к 1. К сожалению, случаи, когда значения индекса заключены между нулем и единицей, не имеют собственной интерпретации. Даже в случае, когда построенная модель идентична истинной функции распределения вероятностей она не является совершенно согласованной.
заключено между 0 и 1, причем, чем больше совпадений между расчетными и фактическими значениями, тем ближе значение индекса к 1. К сожалению, случаи, когда значения индекса заключены между нулем и единицей, не имеют собственной интерпретации. Даже в случае, когда построенная модель идентична истинной функции распределения вероятностей она не является совершенно согласованной.
Второй критерий принято называть псевдо (pseudo) 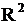 . Его расчет осуществляется по формуле
. Его расчет осуществляется по формуле
 . (3.54)
. (3.54)
Как и в случае индекса  псевдо
псевдо 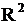 равен 0, когда все коэффициенты модели, кроме
равен 0, когда все коэффициенты модели, кроме  , равны нулю. Его значение приближается к 1 по мере того, как увеличивается разность между
, равны нулю. Его значение приближается к 1 по мере того, как увеличивается разность между  и
и 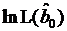 , но самой 1 не достигает. Чем ближе к 1 значение псевдо
, но самой 1 не достигает. Чем ближе к 1 значение псевдо 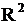 , тем точнее модель воспроизводит фактические значения бинарной переменной.
, тем точнее модель воспроизводит фактические значения бинарной переменной.
3.3.2. Статистическая значимость коэффициентов. Проверка статистической значимости отдельных коэффициентов модели осуществляется с помощью статистики Вальда. Для вычисления ее значения необходимо иметь стандартные ошибки коэффициентов модели. Стандартные ошибки, как и в случае линейной регрессии, определяются по диагональным элементам ковариационной матрицы оценок  . Но прежде, чем перейти к определению значимости, исследуем вопрос состоятельности и асимптотической нормальности этих оценок.
. Но прежде, чем перейти к определению значимости, исследуем вопрос состоятельности и асимптотической нормальности этих оценок.
Известно, что решение любого из уравнений правдоподобия (3.1) или (3.2), даже если оно существует, не обязательно имеет хорошие асимптотические свойства. Желаемые состоятельность и асимптотическая нормальность обеспечены только в том случае, когда выполняются определенные условия, налагаемые на поведение объясняющих переменных в генеральной совокупности. Существуют два подхода к этой проблеме:
1) полагают, что объясняющие переменные являются стохастическими. Тогда налагаемые на них условия предстают в форме «все х i являются независимыми, одинаково распределенными случайными переменными, для которых существуют моменты достаточно высокого порядка»;
2) полагают, что объясняющие переменные фиксированы. В этом случае условия будут следующими:
§ для зависимой переменной 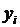 существует асимптотическая матрица вариации-ковариации;
существует асимптотическая матрица вариации-ковариации;
§ значения независимых переменных  ограничены, то есть всегда найдутся такие константы m, M; m > -¥, M < ¥, что:
ограничены, то есть всегда найдутся такие константы m, M; m > -¥, M < ¥, что: 
Если одно из этих условий выполнено, то при достаточно больших n оценка  существует и сходится по вероятности к истинному значению b. Ковариационная матрица этой оценки равняется матрице, обратной к информационной матрице Фишера, которая представляет собой математическое ожидание Гессиана, взятое с обратным знаком
существует и сходится по вероятности к истинному значению b. Ковариационная матрица этой оценки равняется матрице, обратной к информационной матрице Фишера, которая представляет собой математическое ожидание Гессиана, взятое с обратным знаком
 . (3.55)
. (3.55)
Предполагается, что математическое ожидание здесь берется условно по х.
Таким образом, при выполнении выше сформулированных условий можно считать, что оценка вектора коэффициентов модели, полученная с помощью метода максимального правдоподобия, является асимптотически нормальной, т.е.
 . (3.56)
. (3.56)
Как нетрудно понять асимптотическая матрица ковариации зависит от неизвестного параметра b. Поэтому непосредственное использование ее в практических расчетах исключено. Рекомендации здесь те же самые, что и при использовании обычной регрессии – неизвестные параметры, присутствующие в матрице следует заменить соответствующими оценками. Руководствуясь этим общим правилом, можно записать
 (3.57)
(3.57)
и использовать в практических расчетах не ковариационную матрицу, а ее оценку.
Рассмотрим детально, каким образом может быть получена оценка этой матрицы. Для этого вычислим матрицу вторых производных (Гессиан)


 (3.58)
(3.58)
где F = F(x i b) и f = f(x i b).
Для получения информационной матрицы Фишера необходимо Гессиан умножить на минус единицу и взять математическое ожидание. Используя тот факт, что E(yi) = F (x i b), и, проведя несложные преобразования, получаем:
 (3.59)
(3.59)
Соответственно асимптотическая матрица вариации-ковариации  примет вид:
примет вид:
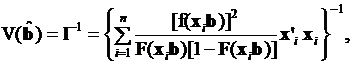 (3.60)
(3.60)
а ее оценка равна
 (3.61)
(3.61)
Корни квадратные из диагональных элементов этой матрицы  являются стандартными ошибками соответствующих оценок
являются стандартными ошибками соответствующих оценок  . Их используют для получения статистики Вальда
. Их используют для получения статистики Вальда
 ,
, 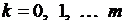 . (3.62)
. (3.62)
В случае логит-модели, для которой  , матрица Фишера упрощается
, матрица Фишера упрощается
 (3.63)
(3.63)
Кроме того, матрицу Фишера можно представить в более компактной и более удобной для расчетов форме.
С этой целью обозначим через  матрицу наблюдений за экзогенными переменными, дополненную столбцом из единиц и имеющую размер
матрицу наблюдений за экзогенными переменными, дополненную столбцом из единиц и имеющую размер 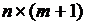 . По-прежнему
. По-прежнему 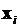 будет обозначать
будет обозначать 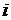 -ую строку матрицы наблюдений. Далее через
-ую строку матрицы наблюдений. Далее через  обозначим диагональную матрицу
обозначим диагональную матрицу  -го порядка, у которой
-го порядка, у которой 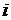 -ый элемент диагонали имеет следующий вид:
-ый элемент диагонали имеет следующий вид:
 . (3.64)
. (3.64)
Тогда информационная матрица Фишера может быть записана следующим образом:
 . (3.65)
. (3.65)
Ковариационная матрица в этом случае равна
 . (3.66)
. (3.66)
Такая форма ковариационной матрицы напоминает обобщенную оценку наименьших квадратов.
3.3.3. Стандартные ошибки предсказанных вероятностей и предельных эффектов. Расчетные значения  , получаемые с помощью оцененных пробит- и логит моделей, представляют собой вероятности того, что переменная
, получаемые с помощью оцененных пробит- и логит моделей, представляют собой вероятности того, что переменная  примет значение 1 или 0. Возможные изменения этих вероятностей в зависимости от факторов оцениваются частными предельными эффектами
примет значение 1 или 0. Возможные изменения этих вероятностей в зависимости от факторов оцениваются частными предельными эффектами
 . (3.67)
. (3.67)
Это именно те характеристики, которые подлежат интерпретации и практическому использованию. Чтобы иметь представление о надежности выводов полученных на основе результатов моделирования необходимо иметь оценки стандартных ошибок этих характеристик. Получить оценки стандартных ошибок можно с помощью дельта метода [63].
Для расчетной вероятности  дельта-метод позволяет записать асимптотическую величину стандартной ошибки в виде
дельта-метод позволяет записать асимптотическую величину стандартной ошибки в виде
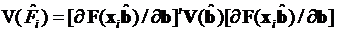 , (3.68)
, (3.68)
где  – асимптотическая ковариационная матрица оценки
– асимптотическая ковариационная матрица оценки  и производная вычислена в точке, компоненты которой совпадают с компонентами оценки
и производная вычислена в точке, компоненты которой совпадают с компонентами оценки  .
.
Заметим, что доступность практического использования данной формулы гарантируется тем, что асимптотическую ковариационную матрицу в ней, следуя рекомендациям предыдущего параграфа, можно заменить оценкой 
Чтобы сделать эту формулу более удобной для расчетов, проведем ее преобразование. С этой целью введем обозначение: 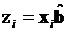 . Тогда вектор производных может быть представлен следующим образом:
. Тогда вектор производных может быть представлен следующим образом:
 . (3.69)
. (3.69)
Замена в (3.68) вектора производных на (3.69) позволяет записать выражение для стандартной ошибки расчетной вероятности  в более компактной форме
в более компактной форме
 . (3.70)
. (3.70)
Стандартная ошибка зависит от вектора, по которому рассчитывалась вероятность.
Теперь перейдем к рассмотрению предельных эффектов. Для удобства введем обозначение  . Тогда асимптотическая ковариационная матрица предельных эффектов может быть записана в виде:
. Тогда асимптотическая ковариационная матрица предельных эффектов может быть записана в виде:
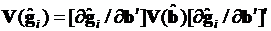 . (3.71)
. (3.71)
Для дальнейших преобразований матрицу производных представим в виде суммы
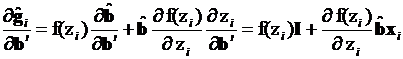 . (3.72)
. (3.72)
В полученном выражении вычисление производной  привело к единичной матрице, а вычисление
привело к единичной матрице, а вычисление 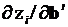 – к вектор-строке
– к вектор-строке 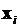 .
.
Для пробит-модели, если учесть, что  , (3.72) переписывается следующим образом:
, (3.72) переписывается следующим образом:
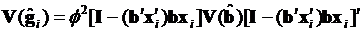 . (3.73)
. (3.73)
В случае логит-модели плотность вероятности  может быть записана через функцию распределения
может быть записана через функцию распределения  как
как  . Для краткости мы будем писать
. Для краткости мы будем писать  , полагая
, полагая  . Дифференцируя это выражение по
. Дифференцируя это выражение по  , получаем
, получаем
 . (3.74)
. (3.74)
Подставляя полученное выражение в (3.72), получаем стандартные ошибки предельных эффектов логит-модели
 . (3.75)
. (3.75)
Стандартные ошибки предельных эффектов, так же как и стандартные ошибки расчетных вероятностей зависят от вектора экзогенных переменных.
3.3.4. Тесты для проверки линейных гипотез. Описанные выше алгоритмы дают оценки, которые являются асимптотически нормальными при стремлении размера выборки к бесконечности. Асимптотическая нормальность оценок обеспечивает корректность проверки линейных гипотез относительно коэффициентов модели. Опорным элементом всех статистиках, используемых в этих тестах, является информационная матрица Фишера. Способ получения асимптотической оценки этой матрицы был рассмотрен выше. Поэтому в дальнейшем изложении предполагается, что матрица Фишера нам известна.
Во всех тестах проверяется нулевая гипотеза, формальная запись которой имеет следующий вид:
 , (3.76)
, (3.76)
где  – вектор тестируемых параметров;
– вектор тестируемых параметров;
 – матрица (размером
– матрица (размером 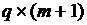 ), задающая структуру ограничений,
), задающая структуру ограничений,
 – вектор (размером
– вектор (размером  ) правой части ограничивающих условий.
) правой части ограничивающих условий.
Все ниже рассматриваемые тесты асимптотически эквивалентны и, следовательно, обеспечивают получение одних и тех же выводов. Поэтому выбор того или иного теста диктуется только конкретной ситуацией и удобством применения в ней.
Тест Вальда. В соответствии спредположением, лежащим в основе теста Вальда, вектор оценок  при выполнении нулевой гипотезы должен быть близок к
при выполнении нулевой гипотезы должен быть близок к  .
.
В силу асимптотической нормальности 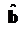 в тех случаях, когда имеет место нулевая гипотеза (
в тех случаях, когда имеет место нулевая гипотеза ( ), случайное отклонение
), случайное отклонение  нормально распределено, т.е.
нормально распределено, т.е.
 , (3.77)
, (3.77)
где  – матрица вариации-ковариации
– матрица вариации-ковариации  , вычисляемая как обратная к информационной матрице Фишера.
, вычисляемая как обратная к информационной матрице Фишера.
Статистика Вальда в этом случае имеет вид
 . (3.78)
. (3.78)
В силу свойств нормального распределения статистика  имеет распределение
имеет распределение  , и проверка нулевой гипотезы осуществляется по правилу
, и проверка нулевой гипотезы осуществляется по правилу

Рассмотрим пример, иллюстрирующий технику проверки предположений относительно коэффициентов модели с помощью теста Вальда. Пусть, например, методом максимального правдоподобия получен вектор оценок  и требуется проверить предположение о том, что
и требуется проверить предположение о том, что 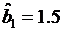 , а
, а  . В этом случае нулевая гипотеза записывается следующим образом:
. В этом случае нулевая гипотеза записывается следующим образом:
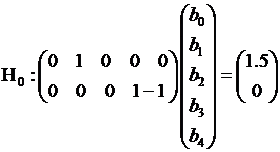
Если проверяется статистическая значимость отдельного коэффициента модели, например  , то, как нетрудно понять, нулевая гипотеза записывается в виде
, то, как нетрудно понять, нулевая гипотеза записывается в виде
 ,
,
и статистика Вальда после выполнения всех перемножений оказывается равной квадрату t–статистики

 , (3.79)
, (3.79)
где  – соответствующий диагональный элемент матрицы
– соответствующий диагональный элемент матрицы  .
.
Есть и другая схема вычисления статистики Вальда. Ее использование удобно в тех случаях, когда проверяется только статистическая значимость некоторых коэффициентов, т.е. проверяется гипотеза о равенстве их нулю.
Будем считать, что независимые переменные упорядочены таким образом, что проверка этой гипотезы касается первых  коэффициентов. Для дальнейшего изложения этой схемы разделим вектор коэффициентов на две группы
коэффициентов. Для дальнейшего изложения этой схемы разделим вектор коэффициентов на две группы
 ,
,
где b 1 – q -мерный вектор, а b 2 включает (m – q) элементов. В этом случае проверяется нуль-гипотеза вида
H0: { b 1 = 0 }. (3.80)
Проверке подвергаются оценки, полученные путем максимизации функции правдоподобия 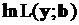 без каких-либо ограничений на оцениваемые коэффициенты модели. Полученные оценки, как отмечалось выше, состоятельны и асимптотически нормальны, т.е.
без каких-либо ограничений на оцениваемые коэффициенты модели. Полученные оценки, как отмечалось выше, состоятельны и асимптотически нормальны, т.е.
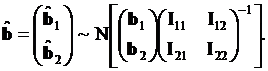 (3.81)
(3.81)
Обращая информационную матрицу, представленную в блочном виде, по частям, получаем для подвектора  матрицу вариации-ковариации
матрицу вариации-ковариации
 (3.82)
(3.82)
Статистика Вальда в этом случае рассчитывается по формуле
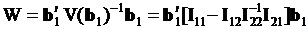 , (3.83)
, (3.83)
и нуль-гипотеза отвергается или нет по результатам сравнения с критическим значением  .
.
Особенность теста Вальда в том, что в нем используются оценки, которые вычислены без учета ограничений, которые постулируются в нуль-гипотезе. Это безусловное достоинство теста, так как для его реализации не требуется проведения дополнительных расчетов.
Тест отношения правдоподобия. В отличие от процедуры Вальда, реализация этого теста требует расчетов, связанных с максимизацией функции правдоподобия без учета ограничений и с учетом ограничений на коэффициенты модели.
Вектор оценок с учетом ограничений имеет вид
 (3.84)
(3.84)
где 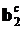 является результатом максимизации
является результатом максимизации  по b 2. Полученная таким образом оценка является состоятельной и асимптотически нормальной:
по b 2. Полученная таким образом оценка является состоятельной и асимптотически нормальной:
 (3.85)
(3.85)
Используемая в тесте статистика основана на сравнении двух оценок максимального правдоподобия, полученных максимизацией ограниченной (с учетом ограничений) и неограниченной (без учета ограничений) функции правдоподобия, т.е.
 . (3.86)
. (3.86)
Статистика имеет распределение  . Поэтому решение о том, отвергнуть или нет нулевую гипотезу, принимается аналогично тому, как это делалось в процедуре Вальда.
. Поэтому решение о том, отвергнуть или нет нулевую гипотезу, принимается аналогично тому, как это делалось в процедуре Вальда.
Тест множителей Лагранжа. Применение этого теста не вызывает затруднений в случае линейных регрессионных моделей. Там понятно, как определить множители Лагранжа и использовать их для расчета статистики. В случае бинарных моделей определение множителей Лагранжа не совсем простая процедура. Поэтому построение статистики основано на других принципах.
Если нулевая гипотеза верна, то две оценки неограниченная  и ограниченная
и ограниченная  должны быть очень близки. Из близости оценок следует близость уравнений правдоподобия, решение которых позволило получить эти оценки.
должны быть очень близки. Из близости оценок следует близость уравнений правдоподобия, решение которых позволило получить эти оценки.
Причем, неограниченная оценка  получена как решение системы уравнений
получена как решение системы уравнений

(3.87)
а ограниченная  – как решение той же самой системы, но с учетом ограничения
– как решение той же самой системы, но с учетом ограничения 
 (3.88)
(3.88)
Обе системы уравнений представляют собой математические ожидания соответствующих уравнений правдоподобия. Взятие математического ожидания в данном случае эквивалентно замене каждой случайной величины 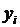 ее ожидаемым значением
ее ожидаемым значением  или
или  , соответственно. Причем, значения самих производных вычислены в точке
, соответственно. Причем, значения самих производных вычислены в точке  .
.
Для рассматриваемого случая статистика множителей Лагранжа записывается следующим образом:
 . (3.89)
. (3.89)
Она является асимптотически эквивалентной статистике Вальда  и статистике отношения правдоподобия
и статистике отношения правдоподобия  и имеет распределение
и имеет распределение  . Решение, отвергнуть нулевую гипотезу или нет, принимается по результатам сравнения с критическим значением
. Решение, отвергнуть нулевую гипотезу или нет, принимается по результатам сравнения с критическим значением  , т.е. процедура сравнения проводится точно так же, как это описано в тесте Вальда.
, т.е. процедура сравнения проводится точно так же, как это описано в тесте Вальда.
Можно значительно упростить процедуру расчета статистики множителей Лагранжа, сведя ее к построению регрессионного уравнения. Правда, для этого необходимо провести ряд не совсем простых преобразований, которые приведут к упрощенной схеме. Начнем с того, что  являясь частью матрицы, обратной информационной матрице Фишера, позволяет записать статистику множителей Лагранжа в эквивалентном виде
являясь частью матрицы, обратной информационной матрице Фишера, позволяет записать статистику множителей Лагранжа в эквивалентном виде
 (3.90)
(3.90)
Теперь вставим индивидуальные наблюдения в уравнение правдоподобия, которое после этой операции будет записываться как сумма логарифмов
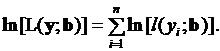 (3.91)
(3.91)
Если наблюдения не коррелированны между собой, то можно показать, что информационная матрица Фишера представима в виде произведения производных первого порядка. Первая производная равна

 . (3.92)
. (3.92)
Соответственно вторая производная может быть записана как


 . (3.93)
. (3.93)
Выполним операцию взятия математического ожидания путем замены 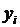 на
на 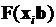 (
( )
)
 .
.
В результате проведенного преобразования взаимно уничтожаются слагаемые, содержащие 
 .
.
Если в преобразованном выражении убрать оператор ожидания, т.е. в числителе снова вернуться к 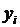

то получаем выражение, отрицательное значение которого представимо в виде суммы произведений
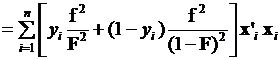 =
=
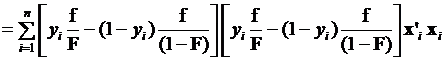 . (3.94)
. (3.94)
Возможность такого представления непосредственно следует из того, что  и
и  , а правильность проверяется непосредственным перемножением.
, а правильность проверяется непосредственным перемножением.
Таким образом, состоятельная оценка информационной матрицы Фишера может быть представлена в виде
 . (3.95)
. (3.95)
Используя полученную оценку информационной матрицы, запишем статистику множителей Лагранжа

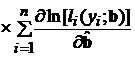 . (3.96)
. (3.96)
Упрощенный расчет этой статистики можно осуществить следующим образом. Обозначим через  матрицу (размером n x q) из соответствующих значений частных производных первого порядка
матрицу (размером n x q) из соответствующих значений частных производных первого порядка
 (3.97)
(3.97)
и через е n -мерный вектор из единиц.
Тогда искусственная линейная регрессия
 (3.98)
(3.98)
с вектором коэффициентов
 (3.99)
(3.99)
может использоваться для расчета статистики  . Коэффициенты такой регрессии легко рассчитываются с помощью любого статистического пакета, а значение статистики равно сумме расчетных значений этой регрессии.
. Коэффициенты такой регрессии легко рассчитываются с помощью любого статистического пакета, а значение статистики равно сумме расчетных значений этой регрессии.



 , (3.53)
, (3.53) – максимальное значение логарифмической функции правдоподобия, достигаемое в точке, координаты которой равны оценкам параметров модели
– максимальное значение логарифмической функции правдоподобия, достигаемое в точке, координаты которой равны оценкам параметров модели  , а
, а 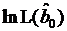 – значение логарифмической функции правдоподобия, вычисленное в предположении, что
– значение логарифмической функции правдоподобия, вычисленное в предположении, что  . (Во многих пакетах предусмотрен расчет этих значений функции правдоподобия).
. (Во многих пакетах предусмотрен расчет этих значений функции правдоподобия). , равны нулю, индекс отношения правдоподобия тоже равен нулю. Если же модель оказалась такой, что ее расчетные значения
, равны нулю, индекс отношения правдоподобия тоже равен нулю. Если же модель оказалась такой, что ее расчетные значения 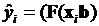 в точности совпадают с наблюдаемыми значениями
в точности совпадают с наблюдаемыми значениями 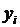 , т.е. имеют место только случаи или
, т.е. имеют место только случаи или 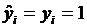 , или
, или  , то индекс
, то индекс  . О такой модели принято говорить, что она совершенно согласована. В остальных случаях значение
. О такой модели принято говорить, что она совершенно согласована. В остальных случаях значение  заключено между 0 и 1, причем, чем больше совпадений между расчетными и фактическими значениями, тем ближе значение индекса к 1. К сожалению, случаи, когда значения индекса заключены между нулем и единицей, не имеют собственной интерпретации. Даже в случае, когда построенная модель идентична истинной функции распределения вероятностей она не является совершенно согласованной.
заключено между 0 и 1, причем, чем больше совпадений между расчетными и фактическими значениями, тем ближе значение индекса к 1. К сожалению, случаи, когда значения индекса заключены между нулем и единицей, не имеют собственной интерпретации. Даже в случае, когда построенная модель идентична истинной функции распределения вероятностей она не является совершенно согласованной.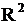 . Его расчет осуществляется по формуле
. Его расчет осуществляется по формуле . (3.54)
. (3.54) . Но прежде, чем перейти к определению значимости, исследуем вопрос состоятельности и асимптотической нормальности этих оценок.
. Но прежде, чем перейти к определению значимости, исследуем вопрос состоятельности и асимптотической нормальности этих оценок. ограничены, то есть всегда найдутся такие константы m, M; m > -¥, M < ¥, что:
ограничены, то есть всегда найдутся такие константы m, M; m > -¥, M < ¥, что: 
 . (3.55)
. (3.55) . (3.56)
. (3.56) (3.57)
(3.57)

 (3.58)
(3.58) (3.59)
(3.59)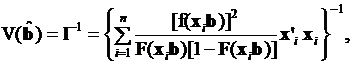 (3.60)
(3.60) (3.61)
(3.61) являются стандартными ошибками соответствующих оценок
являются стандартными ошибками соответствующих оценок  . Их используют для получения статистики Вальда
. Их используют для получения статистики Вальда ,
, 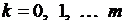 . (3.62)
. (3.62) , матрица Фишера упрощается
, матрица Фишера упрощается (3.63)
(3.63) матрицу наблюдений за экзогенными переменными, дополненную столбцом из единиц и имеющую размер
матрицу наблюдений за экзогенными переменными, дополненную столбцом из единиц и имеющую размер 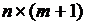 . По-прежнему
. По-прежнему 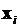 будет обозначать
будет обозначать 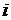 -ую строку матрицы наблюдений. Далее через
-ую строку матрицы наблюдений. Далее через  обозначим диагональную матрицу
обозначим диагональную матрицу  -го порядка, у которой
-го порядка, у которой  . (3.64)
. (3.64) . (3.65)
. (3.65) . (3.66)
. (3.66) , получаемые с помощью оцененных пробит- и логит моделей, представляют собой вероятности того, что переменная
, получаемые с помощью оцененных пробит- и логит моделей, представляют собой вероятности того, что переменная  примет значение 1 или 0. Возможные изменения этих вероятностей в зависимости от факторов оцениваются частными предельными эффектами
примет значение 1 или 0. Возможные изменения этих вероятностей в зависимости от факторов оцениваются частными предельными эффектами . (3.67)
. (3.67) дельта-метод позволяет записать асимптотическую величину стандартной ошибки в виде
дельта-метод позволяет записать асимптотическую величину стандартной ошибки в виде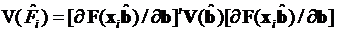 , (3.68)
, (3.68) – асимптотическая ковариационная матрица оценки
– асимптотическая ковариационная матрица оценки 
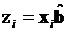 . Тогда вектор производных может быть представлен следующим образом:
. Тогда вектор производных может быть представлен следующим образом: . (3.69)
. (3.69) . (3.70)
. (3.70) . Тогда асимптотическая ковариационная матрица предельных эффектов может быть записана в виде:
. Тогда асимптотическая ковариационная матрица предельных эффектов может быть записана в виде: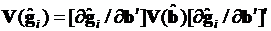 . (3.71)
. (3.71)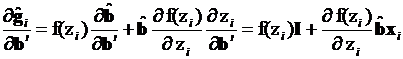 . (3.72)
. (3.72) привело к единичной матрице, а вычисление
привело к единичной матрице, а вычисление 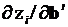 – к вектор-строке
– к вектор-строке  , (3.72) переписывается следующим образом:
, (3.72) переписывается следующим образом: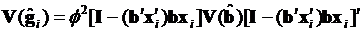 . (3.73)
. (3.73) может быть записана через функцию распределения
может быть записана через функцию распределения  как
как  . Для краткости мы будем писать
. Для краткости мы будем писать  , полагая
, полагая  . Дифференцируя это выражение по
. Дифференцируя это выражение по  , получаем
, получаем . (3.74)
. (3.74) . (3.75)
. (3.75) , (3.76)
, (3.76) – вектор тестируемых параметров;
– вектор тестируемых параметров; – матрица (размером
– матрица (размером 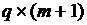 ), задающая структуру ограничений,
), задающая структуру ограничений, – вектор (размером
– вектор (размером  ) правой части ограничивающих условий.
) правой части ограничивающих условий. при выполнении нулевой гипотезы должен быть близок к
при выполнении нулевой гипотезы должен быть близок к 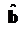 в тех случаях, когда имеет место нулевая гипотеза (
в тех случаях, когда имеет место нулевая гипотеза ( ), случайное отклонение
), случайное отклонение  нормально распределено, т.е.
нормально распределено, т.е. , (3.77)
, (3.77) – матрица вариации-ковариации
– матрица вариации-ковариации  . (3.78)
. (3.78) имеет распределение
имеет распределение  , и проверка нулевой гипотезы осуществляется по правилу
, и проверка нулевой гипотезы осуществляется по правилу
 и требуется проверить предположение о том, что
и требуется проверить предположение о том, что 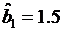 , а
, а  . В этом случае нулевая гипотеза записывается следующим образом:
. В этом случае нулевая гипотеза записывается следующим образом:
 , то, как нетрудно понять, нулевая гипотеза записывается в виде
, то, как нетрудно понять, нулевая гипотеза записывается в виде ,
,
 , (3.79)
, (3.79) – соответствующий диагональный элемент матрицы
– соответствующий диагональный элемент матрицы  коэффициентов. Для дальнейшего изложения этой схемы разделим вектор коэффициентов на две группы
коэффициентов. Для дальнейшего изложения этой схемы разделим вектор коэффициентов на две группы ,
,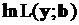 без каких-либо ограничений на оцениваемые коэффициенты модели. Полученные оценки, как отмечалось выше, состоятельны и асимптотически нормальны, т.е.
без каких-либо ограничений на оцениваемые коэффициенты модели. Полученные оценки, как отмечалось выше, состоятельны и асимптотически нормальны, т.е.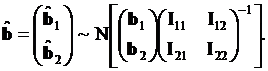 (3.81)
(3.81) матрицу вариации-ковариации
матрицу вариации-ковариации (3.82)
(3.82)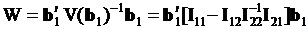 , (3.83)
, (3.83) (3.84)
(3.84)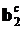 является результатом максимизации
является результатом максимизации  по b 2. Полученная таким образом оценка является состоятельной и асимптотически нормальной:
по b 2. Полученная таким образом оценка является состоятельной и асимптотически нормальной: (3.85)
(3.85) . (3.86)
. (3.86) должны быть очень близки. Из близости оценок следует близость уравнений правдоподобия, решение которых позволило получить эти оценки.
должны быть очень близки. Из близости оценок следует близость уравнений правдоподобия, решение которых позволило получить эти оценки.

 (3.88)
(3.88) или
или  , соответственно. Причем, значения самих производных вычислены в точке
, соответственно. Причем, значения самих производных вычислены в точке  . (3.89)
. (3.89) и имеет распределение
и имеет распределение  , т.е. процедура сравнения проводится точно так же, как это описано в тесте Вальда.
, т.е. процедура сравнения проводится точно так же, как это описано в тесте Вальда. являясь частью матрицы, обратной информационной матрице Фишера, позволяет записать статистику множителей Лагранжа в эквивалентном виде
являясь частью матрицы, обратной информационной матрице Фишера, позволяет записать статистику множителей Лагранжа в эквивалентном виде (3.90)
(3.90)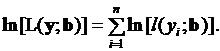 (3.91)
(3.91)
 . (3.92)
. (3.92) . (3.93)
. (3.93)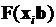 (
( )
) .
.
 .
.
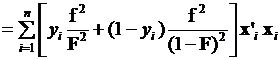 =
=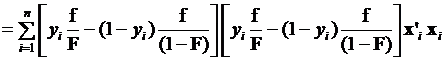 . (3.94)
. (3.94) и
и  , а правильность проверяется непосредственным перемножением.
, а правильность проверяется непосредственным перемножением. . (3.95)
. (3.95)
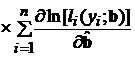 . (3.96)
. (3.96) матрицу (размером n x q) из соответствующих значений частных производных первого порядка
матрицу (размером n x q) из соответствующих значений частных производных первого порядка (3.97)
(3.97) (3.98)
(3.98) (3.99)
(3.99) . Коэффициенты такой регрессии легко рассчитываются с помощью любого статистического пакета, а значение статистики равно сумме расчетных значений этой регрессии.
. Коэффициенты такой регрессии легко рассчитываются с помощью любого статистического пакета, а значение статистики равно сумме расчетных значений этой регрессии.


