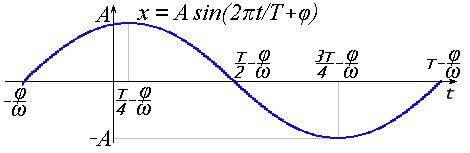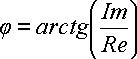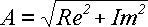Цель работы
Разработка программного генератора псевдослучайных величин, имеющих заданный закон распределения.
Краткие сведения из теории
1. Общая схема реализации случайных величин
Случайная величина (сл.в.) с заданным законом распределения вероятностей всегда может быть получена путем подходящего преобразования стандартного случайного числа. При моделировании на ЭВМ такое подходящее преобразование выполняется над стандартным псевдослучайным числом и в результате получается псевдослучайная величина с требуемым распределением.
2. Метод обращения
Методом обращения можно получить сл.в. x с любой функцией распределения вероятностей (ф.р.в.)  имеющей обратную функцию
имеющей обратную функцию 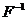 . Метод обращения сводится к тому, чтобы сгенерировать стандартное случайное число z и вычислить x по формуле
. Метод обращения сводится к тому, чтобы сгенерировать стандартное случайное число z и вычислить x по формуле
 (10)
(10)
Тогда сл.в. х будет иметь распределение  .
.
Если на «вход» формулы (10) подавать последовательность  стандартных случайных чисел, то на «выходе» получится последовательность
стандартных случайных чисел, то на «выходе» получится последовательность  независимых сл.в., имеющих ф.р.в.
независимых сл.в., имеющих ф.р.в.  .
.
Для конкретной ф.р.в. F выражение обратной функции 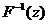 можно получить известным из школьного курса математики способом, состоящим в разрешении уравнения
можно получить известным из школьного курса математики способом, состоящим в разрешении уравнения  относительно x.
относительно x.
Докажем метод обращения. Пусть F – некоторая ф.р.в. Тогда F – монотонно неубывающая функция, принимающая значения в интервале [0,1]. Пусть она имеет обратную функцию 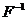 . Определим х через стандартную сл.в. z в виде
. Определим х через стандартную сл.в. z в виде  и найдем ф.р.в.
и найдем ф.р.в.  сл.в. х. По определению
сл.в. х. По определению  (P – вероятность). Но
(P – вероятность). Но 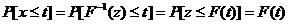 . Таким образом,
. Таким образом,  , что и требовалось.
, что и требовалось.
В качестве примера рассмотрим использование метода обращения для реализации экспоненциальной сл.в.
3. Реализация экспоненциальной сл.в. методом обращения
Ф.р.в. экспоненциальной сл.в.  имеет вид:
имеет вид:
 (11)
(11)
Отсюда 
В соответствии с методом обращения запишем уравнение  или, с учетом (11)
или, с учетом (11)

и, решая его относительно  найдем формулу для генерации сл.в.
найдем формулу для генерации сл.в. 
 (12)
(12)
В полученной формуле разность 1-z, как и сама величина z, является стандартным случайным числом. Этот факт позволяет упростить формулу для генерации  , полагая
, полагая
 (13)
(13)
Назовем экспоненциальную сл.в. с м.о., равным единице, нормированной и обозначим через  . Тогда для
. Тогда для  u=1 и для генерации
u=1 и для генерации  можно использовать формулу
можно использовать формулу
 (14)
(14)
3. Применение линейных преобразований
Под линейным преобразованием (ЛП) сл.в. х будем понимать сл.в. y, полученную из х умножением на константу A и добавлением константы B:

Очевидно,
 ,
,
 (15)
(15)
При построении генераторов сл.в. часто используется свойство ЛП y сохранять вид закона распределения сл.в. х. Так, например, если экспоненциальную сл.в. умножить на константу, то получится снова экспоненциальная сл.в. Нормальная или равномерно распределенная сл.в. не меняет вида закона распределения как при умножении на константу, так и при добавлении константы.
Генератор (14) нормированной экспоненциальной сл.в.  достаточен для реализации экспоненциальных сл.в. с любыми м.о.
достаточен для реализации экспоненциальных сл.в. с любыми м.о. 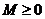 . Для получения экспоненциальной сл.в.
. Для получения экспоненциальной сл.в.  с м.о. M достаточно вычислить ее в виде
с м.о. M достаточно вычислить ее в виде  .
.
Сл.в.  , являющаяся ЛП стандартной сл.в. z, имет равномерное распределение на интервале (B,A+B) и, в соответствии с (15), имеет
, являющаяся ЛП стандартной сл.в. z, имет равномерное распределение на интервале (B,A+B) и, в соответствии с (15), имеет 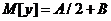 ,
,  .
.
4. Реализация нормальной сл.в. методом суммирования
Плотность распределения вероятностей нормальной сл.в. х с м.о. M и дисперсией  имеет вид:
имеет вид:
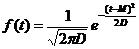 (16)
(16)
Соответствующая ф.р.в

Не выражается в элементарных функциях, что затрудняет непосредственное использование метода обращения. Поэтому для реализации нормальной сл.в. часто применяют метод суммирования, основанный на центральной предельной теореме теории вероятностей. Из этой теоремы вытекает, что сумма Sn достаточно большого числа n стандартных случайных чисел  будет иметь распределение, достаточно близкое к нормальному.
будет иметь распределение, достаточно близкое к нормальному.
Поскольку м.о. суммы Sn и ее дисперсия равны сумме м.о. и сумме дисперсий ее слагаемых, то  . Применим к Sn линейное преобразование, чтобы получить нормированную центрированную сл.в. Х (с м.о. 0 и дисперсией 1). Очевидно для этого надо положить
. Применим к Sn линейное преобразование, чтобы получить нормированную центрированную сл.в. Х (с м.о. 0 и дисперсией 1). Очевидно для этого надо положить  или, заменяя Sn,
или, заменяя Sn,
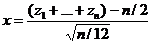 (17)
(17)
На практике часто принимают n=12, т.к. во-первых, при таком числе слагаемых Х имеет распределение, весьма близкое к нормальному, и, во-вторых, значительно упрощается вид формулы (17). При n=12 из (17) получаем формулу для генерации нормированной центрированной сл.в.
 (18)
(18)
Нормальную сл.в. с м.о. M и дисперсией 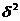 можно получить из
можно получить из  по формуле:
по формуле:

В отличие от метода обращения, метод суммирования является приближенным.
6. Применение функциональных преобразований сл.в.
Часто для реализации сл.в., имеющих сложные законы распределения, можно применять функциональные преобразования сл.в. с простыми распределениями. Это связано с тем, что многие сл.в., широко применяемые в теории вероятностей и математической статистике, вводятся именно как функции других сл.в., которые имеют известные простые законы распределения.
Так, например, эрланговская сл.в., имеющая распределение Эрланга k-го порядка, вводится как сумма k независимых экспоненциальных сл.в. 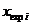 , которые имеют одинаковые м.о.:
, которые имеют одинаковые м.о.:
 (19)
(19)
Эту формулу можно непосредственно использовать для генерации  при наличии генератора для
при наличии генератора для  . Если в (19) суммируются нормированные сл.в.
. Если в (19) суммируются нормированные сл.в.  , то, очевидно,
, то, очевидно,  ,
, 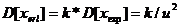
Аналогично сл.в.  (хи-квадрат), имеющая распределение с k степенями свободы, вводится как сумма k независимых сл.в.
(хи-квадрат), имеющая распределение с k степенями свободы, вводится как сумма k независимых сл.в.  , имеющих нормированное центрированное нормальное распределение:
, имеющих нормированное центрированное нормальное распределение:
 (20)
(20)
 .
.
Из (20) ясно, как она может быть реализована при моделировании на ЭВМ.
Распределением Стьюдента с k степенями свободы называют распределение сл.в.
 (21)
(21)
где  - независимые нормированные центрированные нормальные величины.
- независимые нормированные центрированные нормальные величины.
7. Генераторы дискретных сл.в.
Если x – дискретная сл.в., то ее закон распределения вероятностей задается обычно путем указания вероятностей p1,p2… для каждого ее возможного значения x1,x2… соответственно.
Для реализации дискретной сл.в. интервал (0,1) разбивают на подынтервалы  имеющие длину
имеющие длину  . Такое разбиение всегда возможно, поскольку для дискретной сл.в. p1+p2+…=1. Далее сл.в. х может быть сгенерирована по следующему алгоритму:
. Такое разбиение всегда возможно, поскольку для дискретной сл.в. p1+p2+…=1. Далее сл.в. х может быть сгенерирована по следующему алгоритму:
1. генерируется стандартная сл.в. z;
2. определяется номер i подынтервала  , в который попало значение z;
, в который попало значение z;
3. принимается 
В зависимости от значения z сл.в. х будет принимать различные значения из множества  При этом вероятность
При этом вероятность  принять некоторое значение
принять некоторое значение  равно, очевидно, вероятности того, что z попадет в подынтервал
равно, очевидно, вероятности того, что z попадет в подынтервал  , т.е.
, т.е.  . Следовательно
. Следовательно 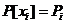 для всех i=1,2,3… Это доказывает, что реализуется сл.в. х с требуемым распределением вероятностей.
для всех i=1,2,3… Это доказывает, что реализуется сл.в. х с требуемым распределением вероятностей.
При моделировании на ЭВМ вместо стандартной сл.в. z используется псевдослучайное число r. Строится сетка из значений вероятностей в зависимости от подынтервала i, точки которой рассчитываются по формуле:
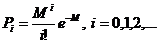 (22)
(22)
Затем генерируется псевдослучайное число r и определяется, в какой интервал оно попало. Очевидно, формула Пуассона подразумевает различные длины интервалов, и в какие-то из них псевдослучайная величина будет попадать чаще, что и позволит построить плотность распределения Пуассона.
Для того, чтобы запрограммировать генерацию чисел по любому закону распределения д.с.в. (в данном случае – Пуассоновский), необходимо:
1. Сгенерировать псевдослучайное число Xi (код можно взять из лаб.1 и 2);
2. После генерации числа, вписать цикл while с условием «пока сгенерированное число Xi больше Pi»;
3. В цикле while рассчитывать значение Pi по формуле (22), с каждым последующим i значение Pi будет расти до тех пор, пока не достигнет Xi;
4. Когда значение Pi превысит сгенерированное число Xi, произойдет выход из цикла;
5. После выхода из цикла while следует зафиксировать последнее значение i (для Pi) и отразить на графике это значение i по горизонтальной оси, и соответствующее ему значение Xi.
6. Повторить пункты 1-5 10000 раз.
Аналогично реализуются генераторы других дискретных псевдослучайных величин, например, бернуллиевская сл.в.  c распределением вероятностей:
c распределением вероятностей:

для нее 
Либо, геометрическое распределение:
 . В данном случае
. В данном случае 
Контрольные вопросы
1. В чем заключается общий принцип реализации случайных (псевдослучайных) величин с заданными законами распределения вероятностей?
2. Как реализуется случайная величина по методу обращения?
3. Как при генерации сл.в. используют линейные преобразования?
4. Как можно реализовать нормальную сл.в.?
5. В каких случаях для реализации сл.в. со сложными законами распределения используются функциональные преобразования сл.в., имеющие более простые распределения?
6. Каким образом можно построить генератор дискретной случайной величины?
Задания к работе
Изучите методы синтеза генераторов сл.в. с заданными законами распределения.
- Напишите программу, реализующую генератор псевдослучайной величины, закон распределения которой указан в табл.1 (для вашего номера варианта), а также генератор чисел, распределенных по закону Пуассона.
Обеспечьте в программе:
- генерацию n значений псевдослучайной величины (рекомендуется n=10000);
- определение и вывод частот встречаемости случайной величины (плотность распределения) на каждом из интервалов и их последующее сравнение со значениями в табл.2 и 3;
- по результатам сравнения с табличными значениями сделайте вывод о соответствии характера распределения случайных величин требуемому закону распределения. Разница между сгенерированными значениями и табличными не должна превышать 0,1.
Отчет должен содержать:
1. цель работы;
2. закон распределения моделируемой случайной величины (указать вариант, формулы);
3. таблицу для сравнения частот встречаемости сл.в. на каждом из интервалов вашего генератора с данными в табл.2 и 3 (при увеличении выборки N, они должны сходиться к вероятностям, указанным в таблицах).
4. скриншоты, на которых будет изображено 4 графика: функция распределения случайной величины и функция плотности распределения вероятностей (для двух законов распределения) как указано в примере (значения, подписанные у графика плотности распределения вероятностей должны сходиться с табличными):

Обратим внимание на данные из таблицы для экспоненциального закона распределения и сравним табличные значения с полученными:
| -
| .6321
| .2325
| .0855
| .0315
| .0116
| .0043
| .0016
| .0006
| .0002
| .0001
|
| -
| .6340
| .2280
| .0880
| .0310
| .0100
| .0050
| .0020
| .0000
| .0000
| .0000
|

Обратим внимание на данные из таблицы для закона Пуассона и сравним табличные значения с полученными:
| .0183
| .0733
| .1465
| .1954
| .1954
| .1563
| .1042
| .0595
| .0298
| .0132
| .0053
|
| .0180
| .0750
| .1420
| .1960
| .1970
| .1520
| .1060
| .0610
| .0330
| .0120
| -
|
5. вывод о соответствии статистических характеристик реализованной псевдослучайной величины требуемым (разница не должна превышать 0,1).
6. Исходный код программы.
| Вариант
| Название распределения вероятностей
| Закон распределения
| Параметры распределения
|
| 1.
| Нормальное
| 
| M – любое (удобнее брать M>3, чтобы избежать работы с отрицательными числами)
D=1
|
| 2.
| Хи-квадрат с k степенями свободы
| 
| k=4
|
| 3.
| Стьюдента с k степенями свободы
| 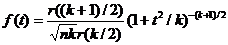
| k=4
|
| 4.
| Экспоненциальное
| 
| u=1
|
| 5.
| Эрланга k-го порядка
| 
| k=3
u=1
|
| Для всех
| Пуассона
| 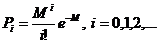
| M=4
|
Табл.1
| (-1,0]
| (0,1]
| (1,2]
| (2,3]
| (3,4]
| (4,5]
| (5,6]
| (6,7]
| (7,8]
| (8,9]
| (9,10]
|
| Нормальное распределение, M=1, D=1:
|
| .3413
| .3413
| .1359
| .0214
| .0013
| .00003
| -
| -
| -
| -
| -
|
| Хи-квадрат:
|
| -
| .0902
| .1740
| .1780
| .1518
| .1187
| .0881
| .0633
| .0443
| .0305
| .0207
|
| Стьюдента с 4 степенями свободы:
|
| .3131
| .3131
| .1288
| .0381
| .0119
| .0044
| .0018
| .0008
| .0004
| -
| -
|
| Экспоненциальное, u=1:
|
| -
| .6321
| .2325
| .0855
| .0315
| .0116
| .0043
| .0016
| .0006
| .0002
| .0001
|
| Эрланга 3 порядка, u=1:
|
| -
| .0803
| .2430
| .2535
| .1851
| .1135
| .0627
| .0323
| .0159
| .0075
| .0035
|
Табл.2
| Вероятности значений 0,…,10 дискретных сл.в.
|
|
|
|
|
|
|
|
|
|
|
|
|
| Распределение Пуассона, m=4:
|
| .0183
| .0733
| .1465
| .1954
| .1954
| .1563
| .1042
| .0595
| .0298
| .0132
| .0053
|
Табл.3
Лабораторная работа 4
Генератор гармонического сигнала. Преобразование Фурье.
Цель работы
Разработка программного генератора гармонического сигнала заданной частоты с функцией разложения сигнала в спектр с помощью дискретного преобразования Фурье (ДПФ).
Краткие сведения из теории
В основе преобразования Фурье (ПФ) лежит чрезвычайно простая, но исключительно плодотворная идея – почти любую периодическую функцию можно представить суммой отдельных гармонических составляющих (синусоид и косинусоид с различными амплитудами A, периодами Т и, следовательно, частотами ω). Пример одной из таких функций S(t), состоящей из гармоник Сi(t), приведен на рис. 1.
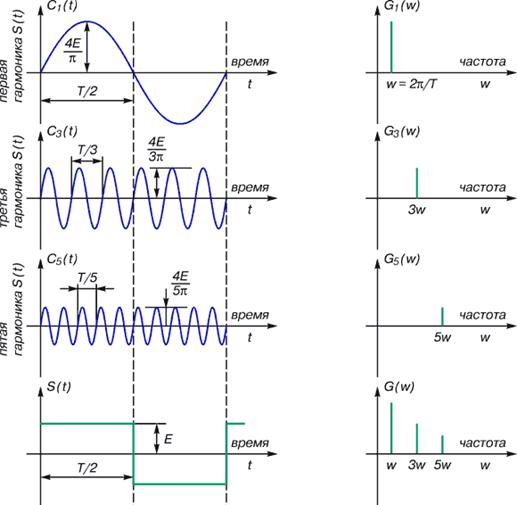
Рис. 1. Представление прямоугольного импульса суммой гармонических составляющих
Понятия «изобразить в частотной области некую функцию от времени» и «нарисовать спектр этой функции» – равнозначны. Если скользнуть по рис. 1 взглядом по горизонтали слева направо, то свершится переход от какой-либо функции времени к ее спектру. А нижняя часть рисунка есть иллюстрация одного из основных принципов ПФ – спектр суммарной функции времени равен сумме спектров ее гармонических составляющих.
Неоспоримым достоинством ПФ является его гибкость – преобразование может использоваться как для непрерывных функций времени, так и для дискретных. В последнем случае оно называется дискретным ПФ – ДПФ.
Для получения дискретной функции времени надо подвергнуть процессу дискретизации непрерывную функцию времени. Это изображено на рис. 2. Вырезаем отдельные значения из непрерывной функции, выстраивая дискретную функцию времени. Период одного цикла его работы называется «периодом дискретизации», или «интервалом дискретности».
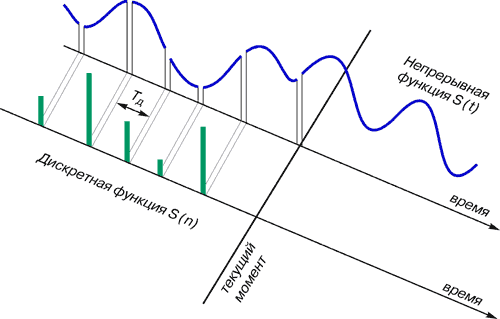
Рис. 2. Дискретное представление непрерывной функции
Одним из ключевых терминов в теории обработки сигналов является понятие о спектре сигнала. Прежде чем пояснить что это такое, введём термин гармонический сигнал. Гармонический сигнал – это сигнал, описываемый функцией синуса (или косинуса). Другими словами, гармонический сигнал может быть представлен следующей формулой
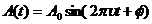 , (1)
, (1)
где  - амплитуда,
- амплитуда,  - частота,
- частота, 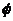 - фаза
- фаза
Ещё одно название данного сигнала – монохроматический.
Важность понятия гармонического сигнала объясняется тем, что любой периодический сигнал (например, последовательность прямоугольных или треугольных импульсов) всегда может быть представлен конечной или бесконечной суммой гармонических сигналов – это есть теорема Фурье о разложение в ряды. Само собой разумеется, что каждый гармонический сигнал (гармоника), входящий в сумму имеет свою амплитуду и значение начальной фазы.
Гармонический сигнал конечной длительности (здесь частота 100 кГц). В повседневной практике – это простейший сигнал синусоидальной формы, который выдаёт генератор частоты, то есть сигнал, имеющий длительность много больше периода синусоиды.

Исходный сигнал

Спектр сигнала
Пусть у нас есть функция синуса x = sin(t).

Максимальная амплитуда этого колебания равна 1. Если умножить его на некоторый коэффициент A, то получим тот же график, растянутый по вертикали в A раз: x = Asin(t).
Период колебания равен 2π. Если мы хотим увеличить период до T, то надо умножить переменную t на коэффициент. Это вызовет растяжение графика по горизонтали: x = A sin(2πt/T).
Частота колебания обратна периоду: ν = 1/T. Также говорят о круговой частоте, которая вычисляется по формуле: ω= 2πν = 2πT. Откуда: x = A sin(ωt).
И, наконец, есть фаза, обозначаемая как φ. Она определяет сдвиг графика колебания влево. В результате сочетания всех этих параметров получается гармоническое колебание или просто гармоника:
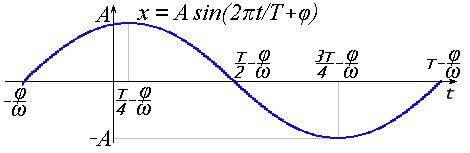
Очень похоже выглядит и выражение гармоники через косинус:
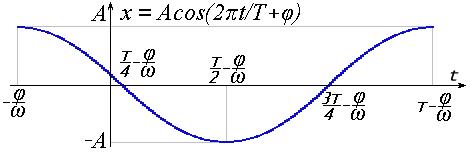
Большой разницы нет. Достаточно изменить фазу на π/2, чтобы перейти от синуса к косинусу и обратно. Далее будем подразумевать под гармоникой функцию косинуса:
x = A cos(2πt/T + φ) = A cos(2πνt + φ) = A cos(ωt + φ) (2)
В природе и технике колебания, описываемые подобной функцией чрезвычайно распространены. Например, маятник, струна, водные и звуковые волны и прочее, и прочее.
Преобразуем (2) по формуле косинуса суммы:
x = A cos φ cos(2πt/T) - A sin φ sin(2πt/T) (3)
Выделим в (3) элементы, независимые от t, и обозначим их как Re и Im:
x = Re cos(2πt/T) - Im sin(2πt / T) (4)
Re = A cos φ, Im = A sin φ
По величинам Re и Im можно однозначно восстановить амплитуду и фазу исходной гармоники:
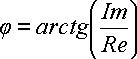
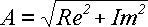
Задание
1. Изучить теоретическую часть;
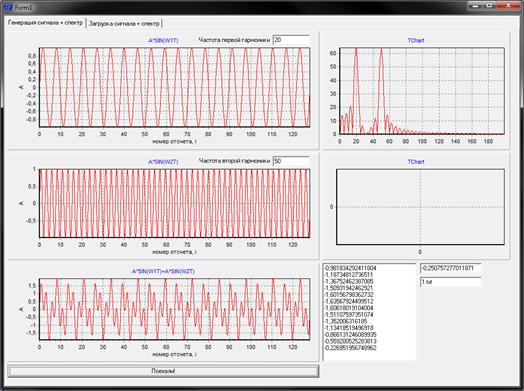
2. Запрограммировать генерацию двух гармонических сигналов заданной частоты (частота – произвольная) и их отображение на двух графиках;
3. Реализовать сигнал, равный сумме двух гармонических сигналов, сгенерированных по п.2;
4. Реализовать разложение итогового сигнала в спектр;
5. Выполнить загрузку файла с сигналом (1280 точек), выданным преподавателем (по вариантам), отобразить его на графике и реализовать его спектральное разложение. Пример:



 имеющей обратную функцию
имеющей обратную функцию 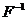 . Метод обращения сводится к тому, чтобы сгенерировать стандартное случайное число z и вычислить x по формуле
. Метод обращения сводится к тому, чтобы сгенерировать стандартное случайное число z и вычислить x по формуле (10)
(10) стандартных случайных чисел, то на «выходе» получится последовательность
стандартных случайных чисел, то на «выходе» получится последовательность  независимых сл.в., имеющих ф.р.в.
независимых сл.в., имеющих ф.р.в. 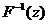 можно получить известным из школьного курса математики способом, состоящим в разрешении уравнения
можно получить известным из школьного курса математики способом, состоящим в разрешении уравнения  относительно x.
относительно x. сл.в. х. По определению
сл.в. х. По определению  (P – вероятность). Но
(P – вероятность). Но 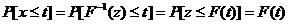 . Таким образом,
. Таким образом,  , что и требовалось.
, что и требовалось. имеет вид:
имеет вид: (11)
(11)
 или, с учетом (11)
или, с учетом (11)
 (12)
(12) (13)
(13) (14)
(14)
 ,
, (15)
(15)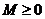 . Для получения экспоненциальной сл.в.
. Для получения экспоненциальной сл.в.  .
. , являющаяся ЛП стандартной сл.в. z, имет равномерное распределение на интервале (B,A+B) и, в соответствии с (15), имеет
, являющаяся ЛП стандартной сл.в. z, имет равномерное распределение на интервале (B,A+B) и, в соответствии с (15), имеет 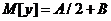 ,
,  .
. имеет вид:
имеет вид: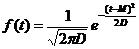 (16)
(16)
 будет иметь распределение, достаточно близкое к нормальному.
будет иметь распределение, достаточно близкое к нормальному. . Применим к Sn линейное преобразование, чтобы получить нормированную центрированную сл.в. Х (с м.о. 0 и дисперсией 1). Очевидно для этого надо положить
. Применим к Sn линейное преобразование, чтобы получить нормированную центрированную сл.в. Х (с м.о. 0 и дисперсией 1). Очевидно для этого надо положить  или, заменяя Sn,
или, заменяя Sn,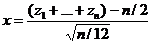 (17)
(17) (18)
(18)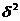 можно получить из
можно получить из  по формуле:
по формуле:
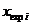 , которые имеют одинаковые м.о.:
, которые имеют одинаковые м.о.: (19)
(19) при наличии генератора для
при наличии генератора для  , то, очевидно,
, то, очевидно,  ,
, 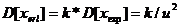
 (хи-квадрат), имеющая распределение с k степенями свободы, вводится как сумма k независимых сл.в.
(хи-квадрат), имеющая распределение с k степенями свободы, вводится как сумма k независимых сл.в.  , имеющих нормированное центрированное нормальное распределение:
, имеющих нормированное центрированное нормальное распределение: (20)
(20) .
. (21)
(21) - независимые нормированные центрированные нормальные величины.
- независимые нормированные центрированные нормальные величины. имеющие длину
имеющие длину  . Такое разбиение всегда возможно, поскольку для дискретной сл.в. p1+p2+…=1. Далее сл.в. х может быть сгенерирована по следующему алгоритму:
. Такое разбиение всегда возможно, поскольку для дискретной сл.в. p1+p2+…=1. Далее сл.в. х может быть сгенерирована по следующему алгоритму: , в который попало значение z;
, в который попало значение z;
 При этом вероятность
При этом вероятность  принять некоторое значение
принять некоторое значение  равно, очевидно, вероятности того, что z попадет в подынтервал
равно, очевидно, вероятности того, что z попадет в подынтервал  . Следовательно
. Следовательно 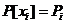 для всех i=1,2,3… Это доказывает, что реализуется сл.в. х с требуемым распределением вероятностей.
для всех i=1,2,3… Это доказывает, что реализуется сл.в. х с требуемым распределением вероятностей.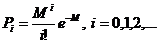 (22)
(22) c распределением вероятностей:
c распределением вероятностей:

 . В данном случае
. В данном случае 




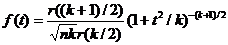




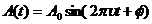 , (1)
, (1) - амплитуда,
- амплитуда,  - частота,
- частота, 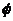 - фаза
- фаза