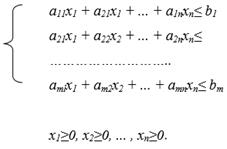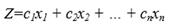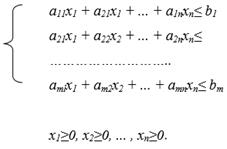Методы выбора альтернатив в условиях определенности

В условиях определенности лицо, принимающее решение, знает все о возможных состояниях сущности явлений, влияющих на решение, и знает, какое решение будет принято. Лицо, принимающее решение, просто выбирает стратегию, направление действий или проект, которые дадут максимальную отдачу.

В общем случае выработка решений в условиях определенности направлена на поиск максимальной отдачи либо в виде максимизации выгоды (дохода, прибыли или полезности), либо минимизации затрат. Такой поиск называется оптимизационным анализом. Три метода оптимизации, используются лицом, принимающим решение: предельный анализ, линейное программирование и приростной анализ прибыли.

Предельный анализ. В условиях определенности доходы и затраты будут известны для любого уровня производства и продаж. Задача состоит в том, чтобы найти их оптимальное соотношение, позволяющее максимизировать прибыль. Предельный анализ позволяет сделать это. В нем используются концепции предельных затрат и предельного дохода (рис.19).

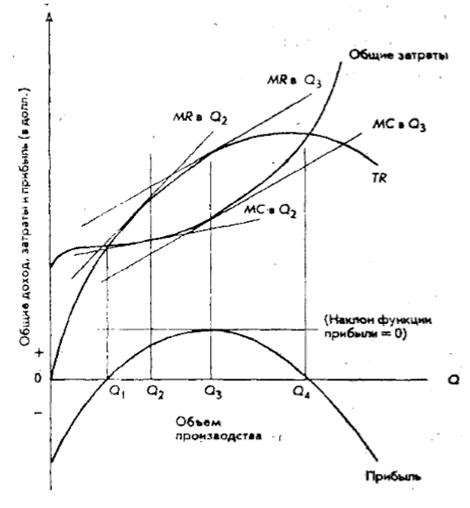
Рис. 19. Концепции предельных затрат и предельного дохода

На этом рисунке представлены кривые дохода, затрат и прибыли, типичные для микроэкономической теории.

Предельный доход (MR) определяется как дополнительный доход (изменение общего дохода), получаемый от продажи дополнительной единицы продукта. Графически он выражается наклоном кривой общего дохода (TR). Предельные затраты (MC) определяются как дополнительные затраты (изменение величины общих затрат) на приобретение или производство дополнительной единицы продукции. Графически они выражаются наклоном кривой общих затрат (TС). Мы должны также отметить следующее.

1. При уровнях производства Q1 и Q4 TR в точности равно ТС, так что прибыль равна нулю. Объем производства меньше Q1 или больше Q4 ведет к убыткам (т.е. характеризуется отрицательной прибылью).

2. При уровнях производства больше Ql или меньше Q4 – прибыль положительная.

3. Предельный анализ показывает, что до тех пор, пока MR превышает МС, производство и продажа дополнительной единицы продукции будут повышать прибыль. Прибыль, соответственно, максимизируется при том уровне производства, при котором MR =МС.

Равенство MR = МС верно при Q3. При этом уровне производства, если мы проведем одну касательную для кривой ТС, а другую – для кривой МС, то мы увидим, что они будут параллельны, т.е. наклоны обеих кривых будут равны между собой. Это означает, что при уровне производства, равном Q3, MR = МС. При таком уровне производства наклон функции прибыли, или предельная прибыль (МР), будет равна нулю.

Приростный анализ. Приростной анализ прибыли оперирует с любыми и всеми изменениями в доходах, затратах и прибылях, явившимися следствием определенного решения. Таким образом, концепция приростного анализа охватывает изменения как самих функций, так и их значений. Основное правило решения состоит в том, чтобы принять любое предложение, повышающее прибыль, или отвергнуть любое предложение, ее уменьшающее.

Линейное программирование. Модели линейного программирования отличаются наглядностью и относительной простотой. Их использование во многих практически важных задачах, связанных с принятием решений, оказалось высокоэффективным, в связи с чем они получили довольно широкое распространение.

К числу наиболее известных задач линейного программирования относятся:

• задачи о распределении ограниченных ресурсов (задачи оптимального планирования);

• задачи об оптимальной корзине продуктов (задачи о диете, задачи оптимального смешения);

• задачи оптимального раскроя (материалов, заготовок);

• транспортные задачи;

• задачи о назначениях;

• задачи оптимизации финансовых потоков;

• задачи оптимизации графиков платежей.

Предприятие может выпускать n видов продукции Р1, Р2,..., Рn, располагая для этого m различными ресурсами R1, R2,..., Rm в количествах b1, b2,...bm соответственно. Известно, что для выпуска единицы продукции Pj необходимо затратить аij единиц ресурса Rij, i = 1, 2,..., m; j = 1, 2,..., n. Кроме того, известен доход от продажи единицы каждого вида продукции – с1, с2,..., сn соответственно, где cj – стоимость единицы продукта Рj например 1 штуки, 1 тонны и т.п.

Требуется так спланировать производственную программу – объемы выпуска каждого вида продукции (в штуках, тоннах и т.п.), чтобы максимизировать доход предприятия. Необходимо найти совокупность значений {x1, х2,..., хn}, обращающих в максимум целевую функцию

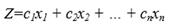
При условии, что переменные {x1, х2,..., хn} удовлетворяют системе ограничений: