Сокращение уровня описания
Наличие диссипативного источника нарушает инвариантность управляющего уравнения относительно инверсии времени. С другой стороны, в состоянии равновесия он должен обращаться в нуль. В этом смысле источниковый член характеризует меру отклонения системы от равновесия. Переход к равновесию осуществляется последовательно через квазиравновесные состояния, каждое из которых характеризуется своей квазиравновесной функцией  . В состоянии равновесия эта функция переходит в равновесную (гиббсовскую). Поэтому, если необходимо описать поведение системы вблизи квазиравновесного состояния
. В состоянии равновесия эта функция переходит в равновесную (гиббсовскую). Поэтому, если необходимо описать поведение системы вблизи квазиравновесного состояния  , источниковый член следует выбрать таким, чтобы он характеризовал степень отклонения системы от этого квазиравновесия. Если еще потребовать, чтобы источник не нарушал линейности уравнения Лиувилля, то необратимое управляющее уравнение можно записать в форме
, источниковый член следует выбрать таким, чтобы он характеризовал степень отклонения системы от этого квазиравновесия. Если еще потребовать, чтобы источник не нарушал линейности уравнения Лиувилля, то необратимое управляющее уравнение можно записать в форме
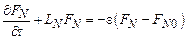 , (11.19)
, (11.19)
где 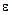 – постоянная, имеющая размерность обратного времени.
– постоянная, имеющая размерность обратного времени.
Уравнение (11.19) обладает 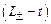 -симметрией и пригодно, следовательно, для описания диссипативных процессов. Такое уравнение впервые было введено Д.Н. Зубаревым. Изучим на его примере специфические черты диссипативной эволюции системы. Проинтегрируем уравнение (11.19)
-симметрией и пригодно, следовательно, для описания диссипативных процессов. Такое уравнение впервые было введено Д.Н. Зубаревым. Изучим на его примере специфические черты диссипативной эволюции системы. Проинтегрируем уравнение (11.19)
 . (11.20)
. (11.20)
При  и
и  мы получили бы расходящееся решение, поэтому значение
мы получили бы расходящееся решение, поэтому значение 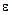 должно быть строго положительным.
должно быть строго положительным.
Выполняя интегрирование по частям, решению (11.20) можно придать вид
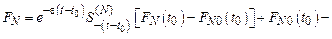
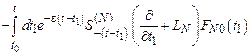 .
.
Первый член в этом выражении связан с начальными данными и экспоненциально затухает, так что при 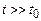 мы приходим к решению
мы приходим к решению
 , (11.21)
, (11.21)
где функция

собственно и описывает неравновесные процессы, происходящие в системе. Таким образом, при 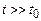 эволюция функции распределения системы целиком зависит от времени квазиравновесной функции. Система «забывает» о части своих начальных данных, а именно о функции
эволюция функции распределения системы целиком зависит от времени квазиравновесной функции. Система «забывает» о части своих начальных данных, а именно о функции  , происходит сокращение уровня описания системы. Указанное сокращение уровня описания происходит на временах
, происходит сокращение уровня описания системы. Указанное сокращение уровня описания происходит на временах 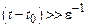 , определяемых параметром
, определяемых параметром 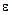 , характеризующим «интенсивность» источника в уравнении (11.19), который, следовательно, имеет смысл обратного времени релаксации системы
, характеризующим «интенсивность» источника в уравнении (11.19), который, следовательно, имеет смысл обратного времени релаксации системы  , т. е. времени «забывания» функции
, т. е. времени «забывания» функции  . С учетом этого уравнение (11.19) можно переписать в форме релаксационного уравнения
. С учетом этого уравнение (11.19) можно переписать в форме релаксационного уравнения
 . (11.22)
. (11.22)
Величина времени релаксации зависит от того, какой является квазиравновесная функция, к какому уровню сокращенного описания мы переходим.
То, от чего получаешь удовольствие или
чем интересуешься, во многом дело вкуса.
…Музыка – один из аспектов гидродинамики.
Д. Перегрин
Феноменологическая гидродинамика
Концепция сплошной среды
Любые жидкость или газ представляют собой систему большого числа частиц, атомов или молекул. Поэтому, в принципе, чтобы описать динамику такой среды, нужно исходить из системы уравнений движения молекул. Такое описание системы мы назвали микроскопическим (см. разд. 7). Очевидно, что реализовать подобный способ описания чрезвычайно сложно из-за огромного числа частиц в системе. Здесь существует, как мы видели, и принципиальное ограничение. Принцип неопределенности Гейзенберга определяет границы точности динамического описания системы взаимодействующих частиц[33]. Следствием этого является важный вывод о том, что всякое динамическое описание системы частиц всегда будет в том или ином смысле огрубленным.
В гидродинамике, равно как и в термодинамике, степень этого огрубления оказывается крайней. Предполагается, что жидкость или газ можно рассматривать как сплошную среду, непрерывный континуум. Динамика системы, жидкости или газа описывается набором нескольких макроскопических наблюдаемых. Их выбор представляется вполне разумным – это плотность, импульс, момент импульса и энергия системы. Как известно из теоретической механики, эти величины в закрытой системе интегрально сохраняются, хотя, если система не находится в равновесии, они локально могут изменяться. Таким образом, задача построения гидродинамического (макроскопического) уровня описания системы состоит в том, чтобы вывести соответствующие уравнения для этих макроскопических переменных и затем решить их.
Прежде чем обсуждать вывод самих уравнений, следует разобраться в том, как определить гидродинамические (макроскопические) переменные. Само понятие макроскопических переменных предполагает, что для описания среды можно выделить некоторые ее характеристики, которые достаточно нечувствительны к изменениям плотности, импульса, момента импульса и энергии, обусловленным индивидуальными движениями молекул. Это означает, что микроскопическими флуктуациями указанных величин можно пренебречь. Каков масштаб таких флуктуаций? Здесь мы подходим к основополагающей идее гидромеханики: концепции сплошной среды. Введение гипотезы сплошности вполне конкретно определяет структуру фазового пространства системы. В частности, это значит, что материальная точка в пространстве, описывающем данную сплошную среду, определяется как физически бесконечно малый объем, т. е. объем, содержащий достаточно большое число молекул. Только в этом случае можно пренебречь указанными флуктуациями. В дальнейшем этот объем будем называть гидродинамическим физически бесконечно малым. Он равен  , где
, где  – гидродинамический физически бесконечно малый масштаб длины. В газе этот масштаб должен удовлетворять условию
– гидродинамический физически бесконечно малый масштаб длины. В газе этот масштаб должен удовлетворять условию
 , (12.1)
, (12.1)
где 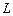 – характерный гидродинамический масштаб течения, а
– характерный гидродинамический масштаб течения, а 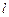 – длина свободного пробега молекул. Естественно требовать равномерности выполнения левого и правого неравенств (12.1),
– длина свободного пробега молекул. Естественно требовать равномерности выполнения левого и правого неравенств (12.1),
 ~
~  ~
~  , и тогда
, и тогда
 и
и 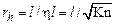 , (12.2)
, (12.2)
где  число Кнудсена. Для сильно неравновесных процессов типа ударной волны, когда
число Кнудсена. Для сильно неравновесных процессов типа ударной волны, когда  , гидродинамический физически бесконечно малый масштаб следует ввести соотноше-нием
, гидродинамический физически бесконечно малый масштаб следует ввести соотноше-нием
 ,
,
где  – физически бесконечно малый масштаб для кинетических процессов, происходящих в газе. Последний для разреженного газа опpеделяется соотношением
– физически бесконечно малый масштаб для кинетических процессов, происходящих в газе. Последний для разреженного газа опpеделяется соотношением 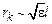 , где
, где  – виpи-альный паpаметp для газа,
– виpи-альный паpаметp для газа, 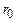 – эффективный pадиус молекулы,
– эффективный pадиус молекулы,  – числовая плотность газа. В этом случае
– числовая плотность газа. В этом случае
 и
и  . (12.3)
. (12.3)
Гидpодинамический физически бесконечно малый масштаб в жидкости будет отвечать иному, нежели в газе, условию
 , (12.4)
, (12.4)
откуда
 . (12.5)
. (12.5)
В соответствии с концепцией сплошной среды макроскопическая (гидродинамическая) наблюдаемая определяется как среднее значение соответствующей динамической величины по гидродинамическому физически бесконечно малому объему. Такое определение соответствует и реализуемой экспериментальной ситуации. Измерение любой макроскопически наблюдаемой величины в жидкости или газе является нелокальным. Прибор всегда дает нам данные, усредненные по некоторому объему, а часто и по времени[34].
Уравнения сохранения
В соответствии с концепцией сплошной среды ее элемент можно охарактеризовать массовой плотностью  . Если величина объема рассматриваемого элемента равна
. Если величина объема рассматриваемого элемента равна  , а ее масса
, а ее масса  , то плотность определяется как предел средней плотности
, то плотность определяется как предел средней плотности
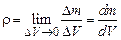 , (12.6)
, (12.6)
так что полная масса определяется интегралом
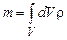 .
.
Изменение массы в рассматриваемом объеме задается уравнением
 , (12.7)
, (12.7)
где мы ввели скорость данного элемента жидкости (его центра масс) 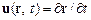 [35]. Если через поверхность
[35]. Если через поверхность 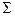 , ограничивающую объем
, ограничивающую объем 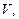 не перетекает вещество, то выражение (3.7) следует приравнять нулю и мы приходим к уравнению сохранения массы или уравнению неразрывности
не перетекает вещество, то выражение (3.7) следует приравнять нулю и мы приходим к уравнению сохранения массы или уравнению неразрывности
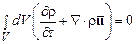 , (12.8)
, (12.8)
которое в силу произвольности рассматриваемого объема эквивалентно дифференциальному уравнению
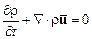 . (12.9)
. (12.9)
Чтобы получить уравнение сохранения импульса, надо учесть, что на выделенный объем жидкости наряду с обычными массовыми силами 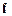 действуют еще поверхностные силы, которые описываются тензором напряжений
действуют еще поверхностные силы, которые описываются тензором напряжений  , т. е. силой, действующей на единицу площади поверхности, ограничивающей рассматриваемый объем. Тогда закон сохранения импульса записывается так:
, т. е. силой, действующей на единицу площади поверхности, ограничивающей рассматриваемый объем. Тогда закон сохранения импульса записывается так:
 . (12.10)
. (12.10)
Используя теорему Гаусса – Остроградского, можно интег-рирование по поверхности в правой части этого уравнения заменить на интегрирование по объему. После чего снова в силу произвольности рассматриваемого объема приходим к следующему уравнению сохранения импульса:
 . (12.11)
. (12.11)
Далее нетрудно убедиться в том, что для среды, элементы которой не имеют собственных моментов импульса, уравнение сохранения момента импульса является простым следствием уравнения (12.11), если только тензор напряжений является симметричным.
Пусть теперь  – внутренняя энергия единицы массы жидкости. Энергия единицы массы объема жидкости
– внутренняя энергия единицы массы жидкости. Энергия единицы массы объема жидкости 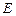 складывается из внутренней и кинетической энергий
складывается из внутренней и кинетической энергий  . Ее изменение во времени в силу закона сохранения энергии равно сумме мощностей массовых и поверхностных сил, приложенных к телу, и потока подводимого к объему тепла
. Ее изменение во времени в силу закона сохранения энергии равно сумме мощностей массовых и поверхностных сил, приложенных к телу, и потока подводимого к объему тепла  :
:
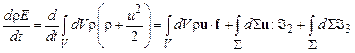 . (12.12)
. (12.12)
Выполняя затем обычные преобразования, приходим к следующему дифференциальному уравнению сохранения энергии:
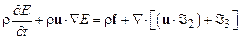 . (12.13)
. (12.13)
Определяющие соотношения
Ньютоновских жидкостей
В жидкости на поверхностях, разделяющих ее элементы, в общем случае возникают нормальные и тангенциальные напряжения. Уравнения переноса (12.9), (12.11), (12.13) только тогда станут собственно уравнениями, когда будет установлена связь между потоками, тензором напряжений и вектором потока тепла, и гидродинамическими переменными[36]. Определяющие соотношения, устанавливающие такую связь, будут зависеть от свойств рассматриваемой среды. В этом разделе мы рассмотрим некоторые наиболее распространенные случаи.
Обычные жидкости являются однородными и изотропными средами. Если предположить, что тангенциальные напряжения, действующие на элемент жидкости, пренебрежимо малы, то тензор напряжений имеет лишь диагональные члены
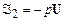 , (12.14)
, (12.14)
где 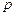 – гидродинамическое давление, а
– гидродинамическое давление, а 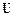 – единичный тензор второго ранга.
– единичный тензор второго ранга.
Что касается недиагональных элементов тензора напряжений, то обычно предполагается, что эти составляющие напряжений диссипативные и обусловлены процессами внутреннего трения в жидкости. Так как внутреннее трение между элементами жидкости возникает лишь в том случае, когда соприкасающиеся слои движутся друг относительно друга, появляющиеся напряжения должны зависеть от градиента скорости. Если предположить, что эта связь линейна, мы приходим к закону вязкого трения Ньютона
 , (12.15)
, (12.15)
где  ,
, 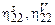 – коэффициенты сдвиговой и объемной вязкостей.
– коэффициенты сдвиговой и объемной вязкостей.
При определении вектора потока тепла обычно используют линейный закон Фурье, постулирующий пропорциональность потока тепла градиенту температуры 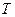 жидкости
жидкости
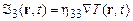 , (12.16)
, (12.16)
где  – коэффициент теплопроводности.
– коэффициент теплопроводности.
Считается, что соотношения (12.15) и (12.16) применимы при достаточно малых градиентах гидродинамических величин. Удовлетворительно интерпретировать их с точки зрения сплошносредного описания не удается, хотя эти соотношения хорошо подтверждаются экспериментально.
Уравнения (12.9), (12.11), (12.13) даже с учетом определяющих соотношений (12.15), (12.16) все еще остаются незамкнутыми. В самом деле, во-первых, последние содержат неизвестные коэффициенты переноса, а, во-вторых, отсутствует уравнение состояния, устанавливающее связь давления с плотностью жидкости и ее температурой (внутренней энергией). Относительно коэффициентов переноса обычно предполагается, что они некоторые константы (или функции температуры[37]), зависящие от свойств жидкости. Уравнение же состояния должно задаваться независимо.
Коэффициенты переноса
При попытке объяснить природу диссипативных процессов в сплошной среде мы сталкиваемся с типичной для гидродинамики пикантной ситуацией: чтобы объяснить диссипацию, необходимо рассмотреть перенос импульса и энергии на молекулярных масштабах, которые в конфигурационном пространстве сплошной среды просто не существуют. Природа и вязкости, и теплопроводности в газах и жидкостях молекулярная, и элементарные соображения о переносе молекулами импульса и энергии приводят нас к законам (12.15) и (12.16). Закон (12.15) легко интерпретируется на примере простого сдвигового потока. Рассмотрим течение газа вдоль оси  со скоростью
со скоростью 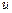 , которая меняется перпендикулярно распространению потока (вдоль оси
, которая меняется перпендикулярно распространению потока (вдоль оси 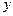 ). Для определенности будем считать, что градиент скорости линеен и направлен снизу вверх. Параллельно оси потока мысленно проведем сечение
). Для определенности будем считать, что градиент скорости линеен и направлен снизу вверх. Параллельно оси потока мысленно проведем сечение 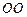 . При тепловом движении молекулы пересекают линию
. При тепловом движении молекулы пересекают линию 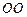 , перенося импульс и энергию. Поток этих молекул пропорционален плотности газа
, перенося импульс и энергию. Поток этих молекул пропорционален плотности газа 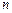 и тепловой скорости молекул
и тепловой скорости молекул  ,
,  (
(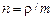 – плотность молекул,
– плотность молекул, 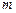 – масса молекулы). Если скорость течения в сечении
– масса молекулы). Если скорость течения в сечении  равна
равна  , то при движении молекулы снизу вверх (ось
, то при движении молекулы снизу вверх (ось 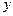 направлена вверх) она переносит тангенциальный импульс, равный
направлена вверх) она переносит тангенциальный импульс, равный
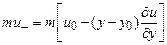 .
.
Поскольку скорость молекул изменяется лишь в результате соударений, то молекула, пересекающая сечение  и переносящая указанный импульс, приобрела свою скорость при предыдущем столкновении, которое произошло на расстоянии порядка средней длины свободного пробега молекулы
и переносящая указанный импульс, приобрела свою скорость при предыдущем столкновении, которое произошло на расстоянии порядка средней длины свободного пробега молекулы  и
и  секунд тому назад (
секунд тому назад ( – среднее время свободного пробега молекул). Таким образом, тангенциальный импульс, переносимый молекулой при движении через сечение
– среднее время свободного пробега молекул). Таким образом, тангенциальный импульс, переносимый молекулой при движении через сечение  снизу вверх, оказывается порядка
снизу вверх, оказывается порядка
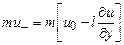 .
.
Аналогично определяется импульс, переносимый молекулой при движении сверху вниз, так что полный переносимый молекулами тангенциальный импульс будет равен
 , (12.17)
, (12.17)
где мы ввели коэффициент вязкости
 . (12.18)
. (12.18)
Рассуждая подобным образом, можно вычислить и перенос энергии через сечение  . Пусть для простоты газ покоится и его температура
. Пусть для простоты газ покоится и его температура  меняется вдоль оси
меняется вдоль оси  . Энергия
. Энергия 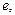 переносимая молекулами через сечение
переносимая молекулами через сечение 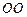 , равна
, равна
 ,
,
где  – удельная теплоемкость, а
– удельная теплоемкость, а
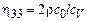 (12.19)
(12.19)
– коэффициент теплопроводности.
Сравнивая определения коэффициентов вязкости и теплопроводности (12.18), (12.19), видим, что они связаны соотношением 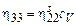 . Отношение коэффициента вязкости жидкости к ее коэффициенту теплопроводности определяется числом Прандтля
. Отношение коэффициента вязкости жидкости к ее коэффициенту теплопроводности определяется числом Прандтля
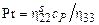 . (12.20)
. (12.20)



 . В состоянии равновесия эта функция переходит в равновесную (гиббсовскую). Поэтому, если необходимо описать поведение системы вблизи квазиравновесного состояния
. В состоянии равновесия эта функция переходит в равновесную (гиббсовскую). Поэтому, если необходимо описать поведение системы вблизи квазиравновесного состояния 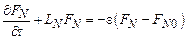 , (11.19)
, (11.19)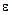 – постоянная, имеющая размерность обратного времени.
– постоянная, имеющая размерность обратного времени.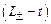 -симметрией и пригодно, следовательно, для описания диссипативных процессов. Такое уравнение впервые было введено Д.Н. Зубаревым. Изучим на его примере специфические черты диссипативной эволюции системы. Проинтегрируем уравнение (11.19)
-симметрией и пригодно, следовательно, для описания диссипативных процессов. Такое уравнение впервые было введено Д.Н. Зубаревым. Изучим на его примере специфические черты диссипативной эволюции системы. Проинтегрируем уравнение (11.19) . (11.20)
. (11.20) и
и  мы получили бы расходящееся решение, поэтому значение
мы получили бы расходящееся решение, поэтому значение 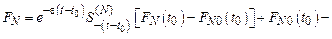
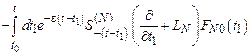 .
.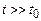 мы приходим к решению
мы приходим к решению , (11.21)
, (11.21)
 , происходит сокращение уровня описания системы. Указанное сокращение уровня описания происходит на временах
, происходит сокращение уровня описания системы. Указанное сокращение уровня описания происходит на временах 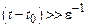 , определяемых параметром
, определяемых параметром  , т. е. времени «забывания» функции
, т. е. времени «забывания» функции  . С учетом этого уравнение (11.19) можно переписать в форме релаксационного уравнения
. С учетом этого уравнение (11.19) можно переписать в форме релаксационного уравнения . (11.22)
. (11.22)
 , где
, где  – гидродинамический физически бесконечно малый масштаб длины. В газе этот масштаб должен удовлетворять условию
– гидродинамический физически бесконечно малый масштаб длины. В газе этот масштаб должен удовлетворять условию , (12.1)
, (12.1)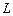 – характерный гидродинамический масштаб течения, а
– характерный гидродинамический масштаб течения, а 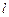 – длина свободного пробега молекул. Естественно требовать равномерности выполнения левого и правого неравенств (12.1),
– длина свободного пробега молекул. Естественно требовать равномерности выполнения левого и правого неравенств (12.1),  ~
~  ~
~  , и тогда
, и тогда и
и 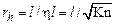 , (12.2)
, (12.2) число Кнудсена. Для сильно неравновесных процессов типа ударной волны, когда
число Кнудсена. Для сильно неравновесных процессов типа ударной волны, когда  , гидродинамический физически бесконечно малый масштаб следует ввести соотноше-нием
, гидродинамический физически бесконечно малый масштаб следует ввести соотноше-нием ,
, – физически бесконечно малый масштаб для кинетических процессов, происходящих в газе. Последний для разреженного газа опpеделяется соотношением
– физически бесконечно малый масштаб для кинетических процессов, происходящих в газе. Последний для разреженного газа опpеделяется соотношением 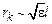 , где
, где  – виpи-альный паpаметp для газа,
– виpи-альный паpаметp для газа, 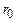 – эффективный pадиус молекулы,
– эффективный pадиус молекулы,  – числовая плотность газа. В этом случае
– числовая плотность газа. В этом случае и
и  . (12.3)
. (12.3) , (12.4)
, (12.4) . (12.5)
. (12.5) . Если величина объема рассматриваемого элемента равна
. Если величина объема рассматриваемого элемента равна  , а ее масса
, а ее масса  , то плотность определяется как предел средней плотности
, то плотность определяется как предел средней плотности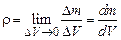 , (12.6)
, (12.6)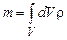 .
. , (12.7)
, (12.7)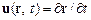 [35]. Если через поверхность
[35]. Если через поверхность 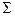 , ограничивающую объем
, ограничивающую объем 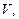 не перетекает вещество, то выражение (3.7) следует приравнять нулю и мы приходим к уравнению сохранения массы или уравнению неразрывности
не перетекает вещество, то выражение (3.7) следует приравнять нулю и мы приходим к уравнению сохранения массы или уравнению неразрывности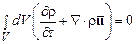 , (12.8)
, (12.8)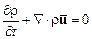 . (12.9)
. (12.9)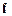 действуют еще поверхностные силы, которые описываются тензором напряжений
действуют еще поверхностные силы, которые описываются тензором напряжений  , т. е. силой, действующей на единицу площади поверхности, ограничивающей рассматриваемый объем. Тогда закон сохранения импульса записывается так:
, т. е. силой, действующей на единицу площади поверхности, ограничивающей рассматриваемый объем. Тогда закон сохранения импульса записывается так: . (12.10)
. (12.10) . (12.11)
. (12.11) – внутренняя энергия единицы массы жидкости. Энергия единицы массы объема жидкости
– внутренняя энергия единицы массы жидкости. Энергия единицы массы объема жидкости 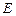 складывается из внутренней и кинетической энергий
складывается из внутренней и кинетической энергий  . Ее изменение во времени в силу закона сохранения энергии равно сумме мощностей массовых и поверхностных сил, приложенных к телу, и потока подводимого к объему тепла
. Ее изменение во времени в силу закона сохранения энергии равно сумме мощностей массовых и поверхностных сил, приложенных к телу, и потока подводимого к объему тепла  :
: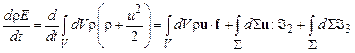 . (12.12)
. (12.12)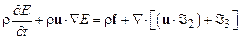 . (12.13)
. (12.13)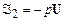 , (12.14)
, (12.14)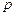 – гидродинамическое давление, а
– гидродинамическое давление, а 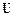 – единичный тензор второго ранга.
– единичный тензор второго ранга. , (12.15)
, (12.15) ,
, 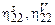 – коэффициенты сдвиговой и объемной вязкостей.
– коэффициенты сдвиговой и объемной вязкостей.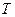 жидкости
жидкости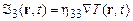 , (12.16)
, (12.16) – коэффициент теплопроводности.
– коэффициент теплопроводности. со скоростью
со скоростью 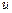 , которая меняется перпендикулярно распространению потока (вдоль оси
, которая меняется перпендикулярно распространению потока (вдоль оси 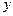 ). Для определенности будем считать, что градиент скорости линеен и направлен снизу вверх. Параллельно оси потока мысленно проведем сечение
). Для определенности будем считать, что градиент скорости линеен и направлен снизу вверх. Параллельно оси потока мысленно проведем сечение 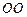 . При тепловом движении молекулы пересекают линию
. При тепловом движении молекулы пересекают линию 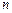 и тепловой скорости молекул
и тепловой скорости молекул  ,
,  (
(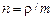 – плотность молекул,
– плотность молекул, 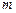 – масса молекулы). Если скорость течения в сечении
– масса молекулы). Если скорость течения в сечении  , то при движении молекулы снизу вверх (ось
, то при движении молекулы снизу вверх (ось 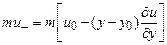 .
. секунд тому назад (
секунд тому назад (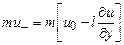 .
. , (12.17)
, (12.17) . (12.18)
. (12.18) меняется вдоль оси
меняется вдоль оси 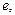 переносимая молекулами через сечение
переносимая молекулами через сечение  ,
, – удельная теплоемкость, а
– удельная теплоемкость, а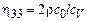 (12.19)
(12.19)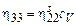 . Отношение коэффициента вязкости жидкости к ее коэффициенту теплопроводности определяется числом Прандтля
. Отношение коэффициента вязкости жидкости к ее коэффициенту теплопроводности определяется числом Прандтля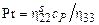 . (12.20)
. (12.20)

