

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Интересное:
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
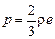 или
или 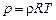 , (13.4)
, (13.4)
где  – так называемая газовая постоянная. Разреженный газ называется также идеальным в отличие от неидеального плотного газа, поскольку взаимодействие молекул не учитывается при написании уравнения состояния (13.4).
– так называемая газовая постоянная. Разреженный газ называется также идеальным в отличие от неидеального плотного газа, поскольку взаимодействие молекул не учитывается при написании уравнения состояния (13.4).
В некоторых случаях, например в изотермических процессах, уравнения состояния (13.4) упрощаются и принимают вид
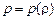 . (13.5)
. (13.5)
Такое уравнение состояния называется уравнением состояния баротропного газа. Частным случаем этого уравнения состояния является уравнение состояния политропного газа
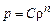 , (13.6)
, (13.6)
где С – некоторая константа, а 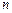 – постоянное число – показатель политропы. Подобное уравнение можно записать и для адиабатических процессов.
– постоянное число – показатель политропы. Подобное уравнение можно записать и для адиабатических процессов.
В плотном газе зависимость давления от плотности и температуры перестает быть линейной (см. уравнение (13.4)). Характер уравнения состояния, вообще говоря, зависит от данного газа и не является универсальным. Однако для широкого класса газов можно использовать так называемое уравнение Ван-дер-Ваальса, которое имеет вид
 .
.
Входящие в это уравнение постоянные  и
и 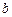 определяются свойствами молекул газа.
определяются свойствами молекул газа.
Распространение малых возмущений в газе.
Скорость звука
Рассмотрим распространение малых возмущений в покоящемся газе. Параметры такого возмущенного движения определяются соотношениями

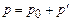 ,
, 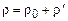 ,
,
где штрихом отмечены возмущенные значения скорости, давления и плотности, а индекс нуль соответствует их невозмущенным значениям. Будем далее предполагать возмущения малыми, т. е.

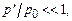
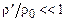 .
.
Переходя к переменным  и линеаризуя уравнения (13.2), в первом приближении получаем
и линеаризуя уравнения (13.2), в первом приближении получаем
|
|
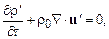
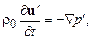
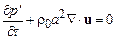 , (13.7)
, (13.7)
где мы ввели скорость звука в газе, определяемую соотношением 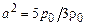 . Из последнего уравнения этой системы легко можно исключить скорость с помощью уравнения сохранения импульса (второго уравнения системы (13.7)). В результате для определения давления получаем волновое уравнение
. Из последнего уравнения этой системы легко можно исключить скорость с помощью уравнения сохранения импульса (второго уравнения системы (13.7)). В результате для определения давления получаем волновое уравнение
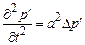 . (13.8)
. (13.8)
Таким образом, эволюция малых возмущений давления (и, как легко установить, скорости и плотности) управляется волновым уравнением, и скорость распространения этого возмущения равна скорости звука.
Волновое уравнение (13.8) допускает две группы решений. Рассмотрим для простоты одномерное распространение возмущений. Тогда эти решения можно представить так:
 ,
,  ,
, 
и
 ,
, 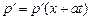 ,
,  .
.
Первая группа описывает возмущения, распространяющиеся в положительном направлении оси  , а другая – в отрицательном. Общее решение указанных волновых уравнений складывается из двух частных, соответствующих указанным двум волнам:
, а другая – в отрицательном. Общее решение указанных волновых уравнений складывается из двух частных, соответствующих указанным двум волнам:
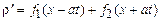 ,
,
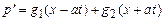 ,
,
 .
.
Типичные для акустики в газе монохроматические звуковые волны описываются функциями вида
 (13.9)
(13.9)
(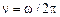 – частота звука, а
– частота звука, а 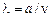 – длина звуковой волны).
– длина звуковой волны).
Человеческое ухо воспринимает звуки с частотами от 20 до
20 000 Гц, что соответствует длинам волн от 15 м до 1,5 см.
Ударные волны
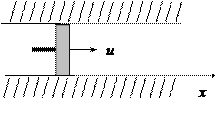 |
 в области, ограниченной слева поршнем, а сверху и снизу – твердыми поверхностями (рис. 13.1). В некоторый начальный момент времени поршень начинает двигаться в положительном направлении оси
в области, ограниченной слева поршнем, а сверху и снизу – твердыми поверхностями (рис. 13.1). В некоторый начальный момент времени поршень начинает двигаться в положительном направлении оси  . Оказывается, эта задача не имеет непрерывного решения. Под действием движущегося поршня возникает так называемая ударная волна. При описании в рамках уравнений Эйлера газодинамические параметры течения терпят разрыв. Перед фронтом
. Оказывается, эта задача не имеет непрерывного решения. Под действием движущегося поршня возникает так называемая ударная волна. При описании в рамках уравнений Эйлера газодинамические параметры течения терпят разрыв. Перед фронтом
Рис. 13.1. Простейшая механическая модель,
в которой реализуется волна
ударной волны газ покоится, а его плотность равна 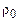 . За фронтом ударной волны скорость газа равна скорости движения поршня
. За фронтом ударной волны скорость газа равна скорости движения поршня 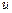 , плотность равна
, плотность равна 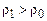 , давление
, давление 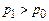 . Течение происходит так, что соотношения параметров перед и за ударной волной определяются законами сохранения, которые можно получить непосредственно из уравнений Эйлера. Чтобы убедиться в этом, будем исходить непосредственно из законов сохранения массы, импульса и энергии[40]:
. Течение происходит так, что соотношения параметров перед и за ударной волной определяются законами сохранения, которые можно получить непосредственно из уравнений Эйлера. Чтобы убедиться в этом, будем исходить непосредственно из законов сохранения массы, импульса и энергии[40]:
|
|
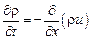 ,
,
 , (13.10)
, (13.10)
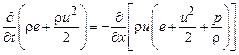 .
.
Предположим сначала, что разрыв – тонкий слой конечной толщины, и проинтегрируем, например, уравнение неразрывности по этому слою от некоторого 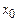 до
до  :
:
 , (13.11)
, (13.11)
а затем перейдем к пределу  . Тогда, поскольку интеграл в левой части пропорционален разности
. Тогда, поскольку интеграл в левой части пропорционален разности 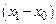 , он стремится к нулю и интегрирование выражения (13.11) дает
, он стремится к нулю и интегрирование выражения (13.11) дает
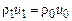 .
.
Аналогично получаются два других закона сохранения:
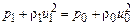 ,
,
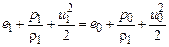 .
.
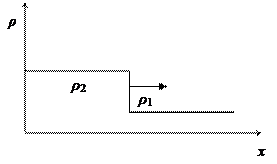 |
Рис. 13.2. Ударная волна в идеальном газе.
Профиль плотности
менее неплохо работает. В силу наличия в реальной среде вязкости и теплопроводности ударная волна представляет собой не контактный разрыв, а слой конечной толщины, причем характерная толщина ударной волны порядка длины свободного пробега молекул газа (см. рис 13.3, на котором представлена зависимость безразмерного профиля ударной волны 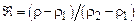 от расстояния
от расстояния 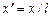 , где
, где 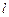 – средняя длина свободного пробега молекул газа). Описать структуру ударной волны не удается и в рамках уравнений Навье – Стокса, поскольку толщина ударной волны порядка длины свободного пробега молекул газа, а на этих масштабах уравнения гидродинамики неприменимы.
– средняя длина свободного пробега молекул газа). Описать структуру ударной волны не удается и в рамках уравнений Навье – Стокса, поскольку толщина ударной волны порядка длины свободного пробега молекул газа, а на этих масштабах уравнения гидродинамики неприменимы.
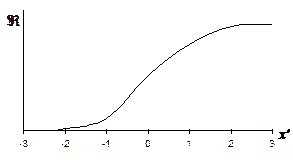 |
Рис. 13.3. Профиль ударной волны (распределение
плотности) в реальном газе
Уравнения (13.2) так же, как уравнения Гамильтона, обратимые уравнения. В них отсутствует диссипация, поэтому они применимы в тех случаях, когда диссипативные эффекты не являются принципиальными на тех временах и пространственных масштабах, на которых данные процессы или явления исследуются. Вязкое трение особенно важно при соприкосновении газа или жидкости с твердыми поверхностями. Поэтому модель идеальной жидкости непригодна для описания течения в тонких слоях вблизи твердых поверхностей, которые называются пограничными слоями. Однако вне пограничных слоев эти уравнения вполне неплохо описывают различные течения. Их нередко применяют и для описания обтекания твердых поверхностей. Вся теория обтекания тонкого профиля, в которой было дано объяснение действующей на него подъемной силы, была построена Н.Е. Жуковским на основе уравнений Эйлера (13.2). При этом, конечно, приходится использовать некоторые дополнительные аксиомы (типа, например, условия Кутта – Жуковского), чтобы не попасть в сети неизбежно возникающих при использовании уравнений Эйлера парадоксов[41].
|
|
…Dum abest qoud avemus, id exsuperare videtur
Cetera; post aliud cum contigit illud avemus,
Et citis aequa tenet[42].
Юлий Цезарь
|
|
|

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!