Уравнение Лиувилля (11.3) описывает эволюцию конечной системы  частиц, находящейся в замкнутом объеме
частиц, находящейся в замкнутом объеме 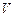 . Такая система называется закрытой. Всякая закрытая система, эволюцию которой мы изучаем, является обычно идеализацией соответствующей физической системы, которую она призвана моделировать. Реально, однако, речь может идти лишь о квазизакрытой системе, поскольку практически всегда существует окружение, оказывающее влияние на рассматриваемую систему. Можно ли пренебречь этим влиянием, и каковы последствия его учета?
. Такая система называется закрытой. Всякая закрытая система, эволюцию которой мы изучаем, является обычно идеализацией соответствующей физической системы, которую она призвана моделировать. Реально, однако, речь может идти лишь о квазизакрытой системе, поскольку практически всегда существует окружение, оказывающее влияние на рассматриваемую систему. Можно ли пренебречь этим влиянием, и каковы последствия его учета?
Взаимодействие частиц системы с окружением приводит к тому, что в уравнении (11.3) появляется дополнительный источниковый член
 , (11.8)
, (11.8)
где 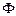 – некоторый оператор. В самом деле, рассмотрим исходную систему
– некоторый оператор. В самом деле, рассмотрим исходную систему  частиц (11.3), имеющую гамильтониан
частиц (11.3), имеющую гамильтониан 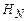 (8.3), и окружение, состоящее из
(8.3), и окружение, состоящее из  взаимодействующих частиц с гамильтонианом
взаимодействующих частиц с гамильтонианом 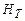 той же структуры, что и (11.3). Взаимодействие системы с окружением описывается гамильтонианом
той же структуры, что и (11.3). Взаимодействие системы с окружением описывается гамильтонианом  . Объединение системы и окружения в свою очередь можно рассматривать как закрытую систему. Ее функция распределения
. Объединение системы и окружения в свою очередь можно рассматривать как закрытую систему. Ее функция распределения 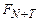 тогда удовлетворяет уравнению Лиувилля
тогда удовлетворяет уравнению Лиувилля
 , (11.9)
, (11.9)
где  – операторы Лиувилля, соответствующие гамильтонианам
– операторы Лиувилля, соответствующие гамильтонианам 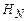 ,
, 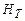 , и
, и  . В общем случае
. В общем случае
 .
.
Функция распределения исследуемой системы  частиц получается из функции
частиц получается из функции 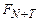 интегрированием по фазовым переменным окружения
интегрированием по фазовым переменным окружения 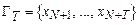
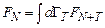 , (11.10)
, (11.10)
 определяет вероятность найти систему в момент времени
определяет вероятность найти систему в момент времени 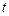 в элементе фазового объема
в элементе фазового объема 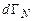 вблизи точки
вблизи точки  независимо от того, как распределены частицы окружения. Проинтегрировав уравнение (11.9) по фазовым переменным окружения, находим
независимо от того, как распределены частицы окружения. Проинтегрировав уравнение (11.9) по фазовым переменным окружения, находим
 . (11.11)
. (11.11)
При выводе последнего уравнения и везде в дальнейшем мы считали, что функция распределения на границах фазового объема обращается в нуль.
Аналогично (11.10) можно ввести функцию распределения окружения
 . (11.12)
. (11.12)
Тогда мерой взаимодействия системы  частиц с окружением будет корреляционная функция
частиц с окружением будет корреляционная функция 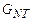 , определяемая соотноше-нием
, определяемая соотноше-нием
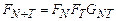 . (11.13)
. (11.13)
Если система не взаимодействует с окружением, то они в любой момент времени статистически независимы и  , а уравнение (11.11) сводится к уравнению Лиувилля (11.3). В общем же случае
, а уравнение (11.11) сводится к уравнению Лиувилля (11.3). В общем же случае 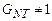 и уравнение (11.11) переходит в уравнение (11.8) с источниковым членом
и уравнение (11.11) переходит в уравнение (11.8) с источниковым членом
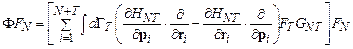 . (11.14)
. (11.14)
Таким образом, функция распределения системы, взаимодействующей с окружением, удовлетворяет уравнению
 ,
, 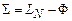 . (11.15)
. (11.15)
Оператор Лиувилля при преобразовании инверсии времени не меняется, что и обеспечивает инвариантность одноименного уравнения (как и уравнений Гамильтона) относительно обращения времени. Эту симметрию уравнения Лиувилля мы будем называть  -симметрией. С уравнением же (11.15) дело обстоит сложнее. В зависимости от характера взаимодействия системы с окружением и формы энергии взаимодействия
-симметрией. С уравнением же (11.15) дело обстоит сложнее. В зависимости от характера взаимодействия системы с окружением и формы энергии взаимодействия  оператор (11.14) может как сохранять
оператор (11.14) может как сохранять  -симметрию, так и нарушать ее. В частности, если выполняется условие четности источникового члена
-симметрию, так и нарушать ее. В частности, если выполняется условие четности источникового члена
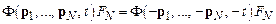 , (11.16)
, (11.16)
 -симметрия уравнения, описывающего взаимодействие системы с окружением, нарушается и уравнение (11.15) становится необратимым. Необратимое управляющее уравнение (11.15), (11.16) обладает особым типом симметрии, которую мы назовем
-симметрия уравнения, описывающего взаимодействие системы с окружением, нарушается и уравнение (11.15) становится необратимым. Необратимое управляющее уравнение (11.15), (11.16) обладает особым типом симметрии, которую мы назовем 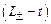 -симметрией, когда часть членов меняет знак при преобразовании инверсии времени, а часть его сохраняет. Наличие
-симметрией, когда часть членов меняет знак при преобразовании инверсии времени, а часть его сохраняет. Наличие 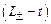 -симметрии и является отличительной чертой необратимых управляющих уравнений. Такие уравнения мы будем называть также диссипативными, а необратимые процессы – диссипативными процессами.
-симметрии и является отличительной чертой необратимых управляющих уравнений. Такие уравнения мы будем называть также диссипативными, а необратимые процессы – диссипативными процессами.
Взаимодействие системы многих частиц с произвольным окружением может быть неконсервативным. Неконсервативными являются, например, взаимодействия между частицами так называемых гранулированных сред. Типичными представителями гранулированных сред являются сахар, песок, зерно и т.п. Полезно поэтому понять, как модифицируется управляющее уравнение для плотности вероятности 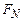 , если на частицы системы наряду с потенциальными действуют и непотенциальные силы. Уравнения движения рассматриваемой системы
, если на частицы системы наряду с потенциальными действуют и непотенциальные силы. Уравнения движения рассматриваемой системы  частиц описываются теперь не гамильтоновой системой уравнений
частиц описываются теперь не гамильтоновой системой уравнений
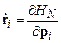 ,
, 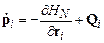 ,
, 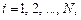 (11.17)
(11.17)
где  – внешняя сила, действующая на
– внешняя сила, действующая на  -ю частицу. В общем случае эта сила является функцией фазовых переменных всех
-ю частицу. В общем случае эта сила является функцией фазовых переменных всех  частиц. Так как число представляющих точек в системе остается неизменным, полная производная по времени от функции распределения
частиц. Так как число представляющих точек в системе остается неизменным, полная производная по времени от функции распределения 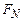 равна нулю, т. е. эта функция удовлетворяет уравнению неразрывности
равна нулю, т. е. эта функция удовлетворяет уравнению неразрывности
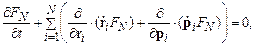
где в скобках стоит 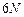 -мерная дивергенция вектора потока «жидкости» представляющих точек ансамбля
-мерная дивергенция вектора потока «жидкости» представляющих точек ансамбля 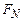 . Подставляя сюда уравнения движения (11.17), сразу находим управляющее уравнение для системы, на которую действуют неконсервативные силы,
. Подставляя сюда уравнения движения (11.17), сразу находим управляющее уравнение для системы, на которую действуют неконсервативные силы,
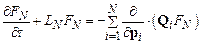 . (11.18)
. (11.18)
В частности, если обобщенная сила  меняет знак при преобразовании инверсии времени, уравнение (11.18) обладает
меняет знак при преобразовании инверсии времени, уравнение (11.18) обладает 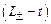 -симметрией, т. е. описывает необратимые процессы. Фазовое пространство системы теперь непрерывно изменяется, а движение представляющей точки происходит по постоянно деформирующейся энергетической гиперповерхности.
-симметрией, т. е. описывает необратимые процессы. Фазовое пространство системы теперь непрерывно изменяется, а движение представляющей точки происходит по постоянно деформирующейся энергетической гиперповерхности.
Мы так много уделяем внимания изучению взаимодействия системы с окружением по той причине, что оно почти всегда приводит к необратимой эволюции системы. Такая эволюция описывается уравнением Лиувилля с источником (11.8). Определение явного вида источника является весьма сложной проблемой. Он будет зависеть от характера окружения, типа действующих на границе сил и т.п. Диссипативное поведение закрытой системы также будет описываться необратимыми управляющими уравнениями вида (11.8) и (11.16). Источник здесь может быть как следствием учета неконтролируемых внешних условий, так и наличием микрофлуктуаций внутри самой системы и эффектами внутренней нелокальности.



 частиц, находящейся в замкнутом объеме
частиц, находящейся в замкнутом объеме 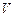 . Такая система называется закрытой. Всякая закрытая система, эволюцию которой мы изучаем, является обычно идеализацией соответствующей физической системы, которую она призвана моделировать. Реально, однако, речь может идти лишь о квазизакрытой системе, поскольку практически всегда существует окружение, оказывающее влияние на рассматриваемую систему. Можно ли пренебречь этим влиянием, и каковы последствия его учета?
. Такая система называется закрытой. Всякая закрытая система, эволюцию которой мы изучаем, является обычно идеализацией соответствующей физической системы, которую она призвана моделировать. Реально, однако, речь может идти лишь о квазизакрытой системе, поскольку практически всегда существует окружение, оказывающее влияние на рассматриваемую систему. Можно ли пренебречь этим влиянием, и каковы последствия его учета? , (11.8)
, (11.8)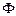 – некоторый оператор. В самом деле, рассмотрим исходную систему
– некоторый оператор. В самом деле, рассмотрим исходную систему 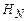 (8.3), и окружение, состоящее из
(8.3), и окружение, состоящее из  взаимодействующих частиц с гамильтонианом
взаимодействующих частиц с гамильтонианом 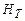 той же структуры, что и (11.3). Взаимодействие системы с окружением описывается гамильтонианом
той же структуры, что и (11.3). Взаимодействие системы с окружением описывается гамильтонианом  . Объединение системы и окружения в свою очередь можно рассматривать как закрытую систему. Ее функция распределения
. Объединение системы и окружения в свою очередь можно рассматривать как закрытую систему. Ее функция распределения 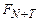 тогда удовлетворяет уравнению Лиувилля
тогда удовлетворяет уравнению Лиувилля , (11.9)
, (11.9) – операторы Лиувилля, соответствующие гамильтонианам
– операторы Лиувилля, соответствующие гамильтонианам  .
.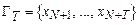
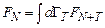 , (11.10)
, (11.10) определяет вероятность найти систему в момент времени
определяет вероятность найти систему в момент времени 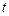 в элементе фазового объема
в элементе фазового объема 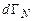 вблизи точки
вблизи точки  независимо от того, как распределены частицы окружения. Проинтегрировав уравнение (11.9) по фазовым переменным окружения, находим
независимо от того, как распределены частицы окружения. Проинтегрировав уравнение (11.9) по фазовым переменным окружения, находим . (11.11)
. (11.11) . (11.12)
. (11.12)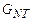 , определяемая соотноше-нием
, определяемая соотноше-нием 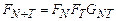 . (11.13)
. (11.13) , а уравнение (11.11) сводится к уравнению Лиувилля (11.3). В общем же случае
, а уравнение (11.11) сводится к уравнению Лиувилля (11.3). В общем же случае 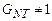 и уравнение (11.11) переходит в уравнение (11.8) с источниковым членом
и уравнение (11.11) переходит в уравнение (11.8) с источниковым членом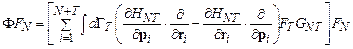 . (11.14)
. (11.14) ,
, 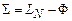 . (11.15)
. (11.15) -симметрией. С уравнением же (11.15) дело обстоит сложнее. В зависимости от характера взаимодействия системы с окружением и формы энергии взаимодействия
-симметрией. С уравнением же (11.15) дело обстоит сложнее. В зависимости от характера взаимодействия системы с окружением и формы энергии взаимодействия 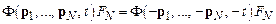 , (11.16)
, (11.16)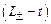 -симметрией, когда часть членов меняет знак при преобразовании инверсии времени, а часть его сохраняет. Наличие
-симметрией, когда часть членов меняет знак при преобразовании инверсии времени, а часть его сохраняет. Наличие 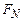 , если на частицы системы наряду с потенциальными действуют и непотенциальные силы. Уравнения движения рассматриваемой системы
, если на частицы системы наряду с потенциальными действуют и непотенциальные силы. Уравнения движения рассматриваемой системы 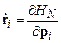 ,
, 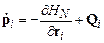 ,
, 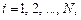 (11.17)
(11.17) – внешняя сила, действующая на
– внешняя сила, действующая на  -ю частицу. В общем случае эта сила является функцией фазовых переменных всех
-ю частицу. В общем случае эта сила является функцией фазовых переменных всех 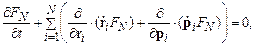
 -мерная дивергенция вектора потока «жидкости» представляющих точек ансамбля
-мерная дивергенция вектора потока «жидкости» представляющих точек ансамбля 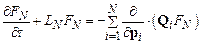 . (11.18)
. (11.18)


