В системе твердых сфер
Метод молекулярной динамики является мощным средством изучения термодинамики исследуемых систем и их свойств переноса. В случае, когда термодинамическая переменная является средним от соответствующей динамической величины (например, энергия), ее определение тривиально. Значительно сложнее провести вычисление величин, в явном виде не имеющих непосредственных микроскопических аналогов. Типичная величина такого типа – термодинамическое давление. Одним из самых распространенных методов расчета давления является использование теоремы вириала, когда давление связывается с изменением импульсов сил в системе.
Для исследования зависимости давления от параметров среды удобно пользоваться безразмерным фактором сжимаемости
 ,
,
где 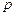 – давление среды;
– давление среды; 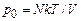 – давление идеального газа;
– давление идеального газа; 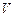 – объем системы, а также приведенной плотностью
– объем системы, а также приведенной плотностью  (напомним, что
(напомним, что  – диаметр молекулы).
– диаметр молекулы).
Типичная зависимость фактора сжимаемости чистого газа твердых сфер от

, полученная методом молекулярной динамики, представлена на рис. 9.3. При исследованных плотностях наблюдается экспоненциальный рост давления с увеличением плотности системы.
Рис. 9.3. Уравнение состояния газа твердых сфер
Одним из наиболее ярких результатов, полученных методом молекулярной динамики, является обнаруженный Б. Олдером и Т. Ванрайтом фазовый переход жидкость – твердое тело для гомогенной системы твердых сфер. Он лучше всего иллюстрируется изотермой при высоких плотностях. Типичный пример такой диаграммы приведен на рис. 9.4. Здесь сплошной линией изображена изотерма однофазной жидкости, иллюстрирующая зависимость коэффициента сжимаемости от плотности упаковки молекул в системе
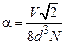 .
.
В чистой однофазной жидкости при увеличении плотности системы коэффициент сжимаемости при некотором значении плотности (см. рис. 9.4) терпит разрыв и при больших плотностях среды переходит на новую ветвь, соответствующую состоянию твердого тела. Это явление и интерпретируется как фазовый переход первого рода.
Рис. 9.4. Изотермы гомогенной и гетерогенной систем в об-
Ласти фазового перехода жидкость – твердое тело: сплош-
ная линия – однонофазная жидкость; штриховая – двухфаз-
ная жидкость; значки – данные эксперимента
Физически фазовый переход в модели твердых сфер объясняется следующим образом. В начальном состоянии молекулы располагаются в узлах плотной гексагональной решетки. Такая упаковка соответствует максимальному среднему расстоянию между соседними молекулами при заданной плотности среды. Добавка в давление, вызванная взаимодействием молекул, при этом минимальна. Если плотность системы достаточно велика, молекула все время остается около узла решетки. Такая среда является аналогом твердого тела. При уменьшении концентрации молекул упорядоченная структура нарушается, система переходит в «жидкое» состояние, давление при этом увеличивается скачкообразно. Доказательство существования фазового перехода жидкость – твердое тело в системе твердых сфер чрезвычайно важно. Оно означает, в частности, что природа такого перехода чисто геометрическая и связана с особенностями упаковки частиц, а не с силами, действующими между ними. Если при малых плотностях молекула могла двигаться по всей ячейке, то после фазового перехода соседние частицы, имеющие определенный размер, не дают ей пройти между собой, и молекула всегда остается вблизи сво-
его начального положения – узла решетки. Это иллюстрирует
рис. 9.5, где приведена зависимость от времени среднего квадрата перемещения отдельной молекулы для двух состояний: до фазового перехода ( ) и после перехода (
) и после перехода ( ). Время измеряется во временах свободного пробега молекул. В жидкости спустя малый начальный период времени зависимость близка к линейной. В твердом теле она ограничена размером зоны (вернее, его квадратом), в которой молекула может передвигаться. Для данной концентрации этот размер довольно велик – около трех диаметров молекулы. С ростом плотности размер этой зоны будет уменьшаться. Для сравнения: в реальном металле с силами молекулярного притяжения плавление начинается при смещении от узла кристаллической решетки атома примерно на 10 % его диаметра.
). Время измеряется во временах свободного пробега молекул. В жидкости спустя малый начальный период времени зависимость близка к линейной. В твердом теле она ограничена размером зоны (вернее, его квадратом), в которой молекула может передвигаться. Для данной концентрации этот размер довольно велик – около трех диаметров молекулы. С ростом плотности размер этой зоны будет уменьшаться. Для сравнения: в реальном металле с силами молекулярного притяжения плавление начинается при смещении от узла кристаллической решетки атома примерно на 10 % его диаметра.
Если в рассматриваемой молекулярной системе одну из молекул заменить ее «тяжелым изотопом» (например, масса замененной молекулы может равняться 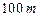 , но радиусы тяжелой и легких молекул одинаковы), то характер наблюдаемого фазового перехода практически не меняется. Коэффициент сжимаемости снова будет описываться сплошной кривой на рис. 9.4.
, но радиусы тяжелой и легких молекул одинаковы), то характер наблюдаемого фазового перехода практически не меняется. Коэффициент сжимаемости снова будет описываться сплошной кривой на рис. 9.4.
Рис. 9.5. Зависимость среднего квадрата отклонения
отдельной молекулы до и после фазового перехода
Характер фазового перехода, однако, существенно изменяется, если в однородную жидкость добавить крупную дисперсную частицу. В расчетах, выполненных автором и его аспирантом А.А. Белкиным и представленных на рис. 9.4, отношение масс частиц и молекул выбиралось равным  , а отношение их радиусов – равным 4. Изотерме описанной гетерогенной системы (жидкость – наночастица) соответствует пунктирная кривая. В ячейке было 2637 молекул. Фазовый переход при наличии в системе дисперсной частицы происходит при бóльших плотностях и давлениях. Плотность, при которой имеет место фазовый переход, повышается. Коэффициент сжимаемости
, а отношение их радиусов – равным 4. Изотерме описанной гетерогенной системы (жидкость – наночастица) соответствует пунктирная кривая. В ячейке было 2637 молекул. Фазовый переход при наличии в системе дисперсной частицы происходит при бóльших плотностях и давлениях. Плотность, при которой имеет место фазовый переход, повышается. Коэффициент сжимаемости  при этом увеличивается с 11,9 до 12,95. Кроме того, в жидком состоянии давление в смеси меньше, чем в однофазной жидкости соответствующей плотности α. В самом деле, в жидком состоянии вся область около частицы доступна для молекул. Введение в однородную молекулярную жидкость дисперсной частицы приводит для несущей молекулярной среды к уменьшению доступного объема ячейки на величину объема частицы и, как следствие, – к уменьшению числа молекул. Значит, дисперсная система в жидком состоянии имеет более низкое давление, нежели однородная, что и показывает рис. 9.4 (правая ветвь изотермы при α > 1,43). Напротив, если смесь остается в твердом состоянии, около частицы образуются экранированные пустые области. Эффективный объем
при этом увеличивается с 11,9 до 12,95. Кроме того, в жидком состоянии давление в смеси меньше, чем в однофазной жидкости соответствующей плотности α. В самом деле, в жидком состоянии вся область около частицы доступна для молекул. Введение в однородную молекулярную жидкость дисперсной частицы приводит для несущей молекулярной среды к уменьшению доступного объема ячейки на величину объема частицы и, как следствие, – к уменьшению числа молекул. Значит, дисперсная система в жидком состоянии имеет более низкое давление, нежели однородная, что и показывает рис. 9.4 (правая ветвь изотермы при α > 1,43). Напротив, если смесь остается в твердом состоянии, около частицы образуются экранированные пустые области. Эффективный объем  частицы в твердом состоянии увеличивается.
частицы в твердом состоянии увеличивается.
Прежде всего во Вселенной хаос зародился.
Гесиод
Компьютерное моделирование
И точность метода
Молекулярной динамики
Вопрос точности при компьютерном моделировании является всегда принципиальным. Метод молекулярной динамики замечателен тем, что позволяет моделировать ситуации, экспериментальное изучение которых затруднено или попросту невозможно. И здесь результаты моделирования приобретают силу экспериментального факта. Естественно, в этом случае вопрос точности полученных результатов оказывается первостепенным. При использовании метода молекулярной динамики можно выделить следующие основные причины появления систематических ошибок:
1) ошибки округления;
2) ошибки, связанные с использованием тех или иных схем численного интегрирования уравнений Ньютона;
3) ошибки, обусловленные конечным размером расчетной ячейки и использованием периодических граничных условий;
4) корреляции, обусловленные конечным числом частиц в моделирующей системе.
Наличие ошибок округления является принципиальным фактором использования для моделирования компьютеров. Поскольку округление чисел происходит случайно, данный тип погрешности, вносимой в расчет, является стохастическим. Наличие именно этого типа погрешностей делает движение системы в фазовом пространстве необратимым. Это подтверждают и непосредственные расчеты. При сравнении динамических траекторий прямого и обратного движений, получаемых при обращении времени (и импульсов всех частиц), можно выделить интервал времени, где отклонение фазовых траекторий прямого и обратного движений отличаются мало. Однако степень этого отклонения со временем быстро нарастает. Ошибки округления приводят к тому, что каждый акт взаимодействия частиц имеет стохастический элемент и в этом смысле взаимодействие перестает быть упругим (даже для упругих твердых сфер!).
Конечную точность представления чисел компьютером особенно важно учитывать при решении эволюционных задач, например, при расчете траекторий молекул. Однако при определении интегральных характеристик, к которым относятся средние времена свободного пробега и релаксации, а также автокорреляционные функции, этот эффект проявляется очень слабо. Так, при расчете коэффициента самодиффузии газа, когда статистическая ошибка мала, различие величин коэффициента самодиффузии, рассчитанных с одинарной и двойной точностью представления чисел, не превышало 0,5 %, при этом данное число включает и статистическую ошибку.
Ошибки, связанные с конечно-разностной аппроксимацией уравнений Ньютона, неизбежны, и степень этих ошибок растет со временем. Поэтому основным критерием использования той или иной конечно-разностной схемы является прежде всего правильность определения доверительного временного интервала, в течение которого эти ошибки остаются достаточно малыми, чтобы существенно не влиять на качество расчета. Если это время равно 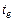 , то ошибки определения динамических переменных
, то ошибки определения динамических переменных 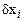 на таких временах должны быть малыми. Поскольку при использовании конечно-разностных схем того или иного порядка ошибка вычисления динамических переменных пропорциональна шагу дискретизации, этот шаг
на таких временах должны быть малыми. Поскольку при использовании конечно-разностных схем того или иного порядка ошибка вычисления динамических переменных пропорциональна шагу дискретизации, этот шаг  должен быть таким, чтобы выполнялось соотношение
должен быть таким, чтобы выполнялось соотношение  , где показатель
, где показатель  определяется порядком используемой схемы. На практике точность решения динамической задачи, как уже отмечалось, можно проверять по выполнению законов сохранения.
определяется порядком используемой схемы. На практике точность решения динамической задачи, как уже отмечалось, можно проверять по выполнению законов сохранения.
В методе молекулярной динамики, где для моделирования применяются твердые сферы, второй пункт появления погрешностей расчета отсутствует и его поэтому можно использовать, в частности, для определения точности тех или иных разностных аппроксимаций уравнений Ньютона.
В связи с тем, что расчетная ячейка имеет конечную длину 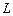 , появляется еще один источник ошибок. В реальном газе или жидкости возмущение, возникшее в некоторой точке, распространяется по всему объему и затем затухает из-за диссипативных эффектов. Размеры расчетной ячейки обычно достаточно малы, и возмущение, появившееся в некоторой точке, спустя время порядка
, появляется еще один источник ошибок. В реальном газе или жидкости возмущение, возникшее в некоторой точке, распространяется по всему объему и затем затухает из-за диссипативных эффектов. Размеры расчетной ячейки обычно достаточно малы, и возмущение, появившееся в некоторой точке, спустя время порядка  может вновь достичь ее. Здесь
может вновь достичь ее. Здесь 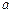 – скорость распространения возмущения, в газах и жидкостях – это скорость звука. Таким образом, гарантированную точность можно ожидать (при прочих равных условиях) лишь на временах порядка
– скорость распространения возмущения, в газах и жидкостях – это скорость звука. Таким образом, гарантированную точность можно ожидать (при прочих равных условиях) лишь на временах порядка 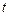 ~
~  .
.
Конечное число частиц  в моделирующей системе становится источником серьезных ошибок в случае, когда моделируемая система большая (бесконечная). Физической причиной появления таких ошибок является то, что в конечной системе развиваются корреляции с характерными временами порядка времени изучения системы, не типичные для моделируемой системы. Корреляции эти в общем случае плохо изучены. Исключение представляет случай разреженного газа, который будет рассмотрен во второй части данного курса. Традиционный и самый простой способ проверки влияния конечного числа частиц на результаты расчета состоит в увеличении
в моделирующей системе становится источником серьезных ошибок в случае, когда моделируемая система большая (бесконечная). Физической причиной появления таких ошибок является то, что в конечной системе развиваются корреляции с характерными временами порядка времени изучения системы, не типичные для моделируемой системы. Корреляции эти в общем случае плохо изучены. Исключение представляет случай разреженного газа, который будет рассмотрен во второй части данного курса. Традиционный и самый простой способ проверки влияния конечного числа частиц на результаты расчета состоит в увеличении  и проверке степени влияния числа частиц на результат. Если результат с достаточной точностью не изменяется, число частиц можно считать вполне достаточным для моделирования. К сожалению, во многих случаях этого не удается сделать, так как исследуются системы с максимально возможным для современных компьютеров числом частиц
и проверке степени влияния числа частиц на результат. Если результат с достаточной точностью не изменяется, число частиц можно считать вполне достаточным для моделирования. К сожалению, во многих случаях этого не удается сделать, так как исследуются системы с максимально возможным для современных компьютеров числом частиц 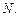 Именно поэтому изучение влияния эффекта конечных
Именно поэтому изучение влияния эффекта конечных  столь необходимо.
столь необходимо.
Ограниченное число частиц в системе и достаточно малые размеры расчетной ячейки делают метод молекулярной динамики пригодным для моделирования лишь жидкостей и очень плотных газов. Для моделирования разреженных газов необходима ячейка размером  , где
, где 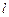 – средняя длина свободного пробега молекул газа. При нормальном давлении
– средняя длина свободного пробега молекул газа. При нормальном давлении 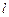 ~10-5 см, а плотность
~10-5 см, а плотность
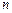 ~1019 молекул на кубический сантиметр. Поэтому число частиц, минимально необходимых для моделирования разреженного газа, порядка
~1019 молекул на кубический сантиметр. Поэтому число частиц, минимально необходимых для моделирования разреженного газа, порядка  ~1010. Это все еще недоступно для современных компьютеров. Однако умеренно плотный газ моделировать уже можно.
~1010. Это все еще недоступно для современных компьютеров. Однако умеренно плотный газ моделировать уже можно.
Метод молекулярной динамики нельзя воспринимать как некое вспомогательное средство для описания гидродинамических течений, в частности, как метод вычисления коэффициентов переноса. Он, конечно, прекрасно справляется с этой задачей, однако его роль и место в современной теории процессов переноса значительно шире. Этот метод позволяет исследовать и равновесные, и неравновесные свойства среды и, что особенно важно, механизмы релаксационных процессов. Этот метод прекрасно зарекомендовал себя при решении самых разных задач теории переноса. Сегодня он имеет нередко доказательную силу эксперимента, а в ряде случаев даже предпочтителен, поскольку очень хорошо приспособлен для проверки конкретных гипотез. С чем же связан такой успех? Выше при обсуждении вопроса точности этого метода мы отметили две характерные особенности. Первая состоит в том, что в методе рассматривается конечная система частиц. В большинстве задач точность определения объемных свойств среды пропорциональна, по-видимому,  . Поэтому точность, достижимая сегодня в обычных гидродинамических и теплофизических экспериментах, достигается уже при сравнительно небольшом числе частиц. Кроме того, конечность числа используемых в методе частиц стимулировала изучение поведения систем конечного числа частиц. Думается, что это самый перспективный метод их изучения. Связано это не только с технической сложностью экспериментального изучения явлений в системах малого числа частиц, хотя такие сложности, конечно, существуют. В некоторых случаях экспериментальное изучение принципиально ограничено, поскольку возмущения, вносимые прибором, оказываются порядка самого эффекта. Так обстоит дело, например, при изучении флуктуаций в малых объемах, которые очень важны, например, при исследовании процессов переноса наночастиц.
. Поэтому точность, достижимая сегодня в обычных гидродинамических и теплофизических экспериментах, достигается уже при сравнительно небольшом числе частиц. Кроме того, конечность числа используемых в методе частиц стимулировала изучение поведения систем конечного числа частиц. Думается, что это самый перспективный метод их изучения. Связано это не только с технической сложностью экспериментального изучения явлений в системах малого числа частиц, хотя такие сложности, конечно, существуют. В некоторых случаях экспериментальное изучение принципиально ограничено, поскольку возмущения, вносимые прибором, оказываются порядка самого эффекта. Так обстоит дело, например, при изучении флуктуаций в малых объемах, которые очень важны, например, при исследовании процессов переноса наночастиц.
В реальных расчетах размер ячейки оказывается порядка десятка или нескольких десятков эффективных размеров молекул. Таким образом, реально изучаемый объем среды имеет характерный масштаб порядка 50…200 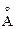 . Поэтому изучаемая система должна быть такой, чтобы данные масштабы были представительны. Использование периодических граничных условий предполагает, что свойства среды одинаковы с периодом, определяемым этими условиями. В твердом теле, где существует собственная периодическая структура, необходимо отслеживать влияние периодических граничных условий на реально существующую периодическую структуру.
. Поэтому изучаемая система должна быть такой, чтобы данные масштабы были представительны. Использование периодических граничных условий предполагает, что свойства среды одинаковы с периодом, определяемым этими условиями. В твердом теле, где существует собственная периодическая структура, необходимо отслеживать влияние периодических граничных условий на реально существующую периодическую структуру.
Характерные времена, на которых данным методом можно получить достоверную информацию, оказываются порядка 10-10 с.
В то же время даже в жидкости гидродинамический физически бесконечно малый масштаб (см. следующий раздел) порядка 10-6 см и характерное время распространения звука на таких масштабах порядка 10-11…10-10 с, т. е. на пределе существующих расчетных возможностей. Поэтому говорить об изучении методом молекулярной динамики гидродинамических явлений следует с большой осторожностью.
Наличие ошибок округления является принципиальным фактором использования метода молекулярной динамики. Вносимые в вычисления погрешности имеют стохастический характер. В результате на каждом шаге решается система стохастических уравнений

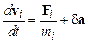 ,
,  (10.1)
(10.1)
где 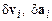 – стохастические составляющие скорости и ускорения частиц системы. Необратимость уравнений (10.1) позволяет вычислить по формулам типа Кубо коэффициенты переноса (коэффициента вязкости, диффузии и т.п.). В противном случае, если бы вычисляемые траектории частиц были обратимыми, соответствующие формулы давали нулевые значения, поскольку обратимое гамильтоново движение системы квазипериодично[32]. Как представляется, само существование коэффициентов переноса в природе является косвенным свидетельством в пользу того, что динамика системы должна описываться уравнениями типа (10.1).
– стохастические составляющие скорости и ускорения частиц системы. Необратимость уравнений (10.1) позволяет вычислить по формулам типа Кубо коэффициенты переноса (коэффициента вязкости, диффузии и т.п.). В противном случае, если бы вычисляемые траектории частиц были обратимыми, соответствующие формулы давали нулевые значения, поскольку обратимое гамильтоново движение системы квазипериодично[32]. Как представляется, само существование коэффициентов переноса в природе является косвенным свидетельством в пользу того, что динамика системы должна описываться уравнениями типа (10.1).
В связи с изложенными соображениями встает вопрос о том, нужно или нет бороться за точность расчетов методом молекулярной динамики. Ответ, безусловно, положительный. Реальные стохастические источники в уравнениях динамики (10.1) достаточно малы, поэтому существование именно таких малых случайных источников и должны учитывать наши компьютерные вычисления. Если ошибки, вносимые в вычисление машиной или программой, будут выше этого некоторого уровня, то мы просто будем решать совсем иную физическую задачу, кстати, тоже имеющую смысл.
Итак, вопросы точности при численном решении любой задачи являются первостепенными. Многие численные решения сегодня имеют доказательную силу эксперимента (метод молекулярной динамики, в частности), и вопрос о том, какую ошибку мы совершаем в расчетах, нуждается в точном и исчерпывающем ответе.
Универсально лишь то,
что достаточно грубо.
Поль Валери
Полевое описание
Систем многих частиц
Уравнения Гамильтона (8.4) с гамильтонианом (8.3) принципиально позволяют изучить эволюцию любой системы. Однако это тот случай, когда от принципиальной возможности до реализации огромная дистанция. Лучше сказать, что эта возможность кажущаяся. И дело даже не в том, что любая макроскопическая система состоит из огромного числа частиц, так что решить соответствующую систему уравнений не под силу самой быстродействующей вычислительной машине. Неприятность состоит в том, что для решения системы уравнений (8.4) необходимо задать начальные условия, т. е. начальные положения и импульсы всех  частиц системы. Задача эта невыполнима технически. Однако есть и принципиальные трудности. Принцип неопределенности Гейзенберга не позволяет сколь угодно точно определить динамические переменные частицы. Мы видели, что система чрезвычайно чувствительна даже к малым вариациям начальных данных. Поэтому требуется некоторый альтернативный способ описания системы многих частиц, свободный от необходимости решать данную проблему. Изложению основ такого описания и посвящен настоящий раздел.
частиц системы. Задача эта невыполнима технически. Однако есть и принципиальные трудности. Принцип неопределенности Гейзенберга не позволяет сколь угодно точно определить динамические переменные частицы. Мы видели, что система чрезвычайно чувствительна даже к малым вариациям начальных данных. Поэтому требуется некоторый альтернативный способ описания системы многих частиц, свободный от необходимости решать данную проблему. Изложению основ такого описания и посвящен настоящий раздел.
Уравнение Лиувилля
Об альтернативном описании систем многих частиц – полевом статистическом описании системы – уже говорилось в разд. 7. При таком описании в 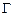 -пространстве вводится
-пространстве вводится  -частичная функция распределения
-частичная функция распределения 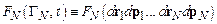 . Эта функция нормирована на единицу (см. соотношение (7.2)) и для системы тождественных частиц симметрична относительно перестановки их фазовых координат.
. Эта функция нормирована на единицу (см. соотношение (7.2)) и для системы тождественных частиц симметрична относительно перестановки их фазовых координат.
Вероятность найти систему в некотором объеме фазового пространства 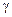 определяется числом представляющих точек в этом объеме и равна
определяется числом представляющих точек в этом объеме и равна
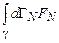 .
.
Эта вероятность, очевидно, задается лишь величиной объема, точнее, числом представляющих точек в объеме 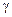 , и не зависит от времени. Поэтому
, и не зависит от времени. Поэтому
 . (11.1)
. (11.1)
Поскольку 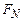 – функция времени и фазовых переменных,
– функция времени и фазовых переменных,
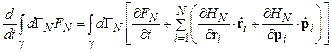 ,
,
а в силу уравнений Гамильтона (8.4)
 .
.
Так как это справедливо для любого объема 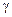 , в нуль должно обращаться подынтегральное выражение, и мы получаем уравнение для функции распределения
, в нуль должно обращаться подынтегральное выражение, и мы получаем уравнение для функции распределения  частиц – уравнение Лиувилля
частиц – уравнение Лиувилля
 .
.
Вводя оператор Лиувилля,
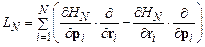 , (11.2)
, (11.2)
уравнение Лиувилля можно записать в компактной форме:
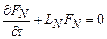 . (11.3)
. (11.3)
Уравнение Лиувилля является следствием одноименной теоремы. Согласно последней фазовый объем системы  частиц, динамика которых определяется уравнениями Гамильтона, не меняется со временем
частиц, динамика которых определяется уравнениями Гамильтона, не меняется со временем
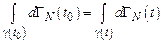 или
или 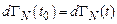 . (11.4)
. (11.4)
Действительно, вероятность нахождения системы в начальный момент времени  в бесконечно малом объеме фазового пространства
в бесконечно малом объеме фазового пространства  равна
равна  . В момент же времени
. В момент же времени 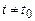 вероятность найти систему в объеме
вероятность найти систему в объеме 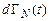 дается выражением
дается выражением
 ,
,
где 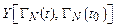 – якобиан преобразования от переменных
– якобиан преобразования от переменных 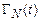 к –
к –  . В силу теоремы Лиувилля (11.4) якобиан
. В силу теоремы Лиувилля (11.4) якобиан 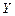 равен единице (это не сложно доказать и непосредственно, используя уравнения Гамильтона), а значит,
равен единице (это не сложно доказать и непосредственно, используя уравнения Гамильтона), а значит, 
 , т. е. функция распределения сохраняется вдоль траектории, а выражением этого факта и является уравнение Лиувилля (11.3).
, т. е. функция распределения сохраняется вдоль траектории, а выражением этого факта и является уравнение Лиувилля (11.3).
Уравнение Лиувилля представляет собой линейное дифференциальное уравнение в частных производных. Задача его интегрирования эквивалентна задаче интегрирования уравнений Гамильтона. Вместе с тем уравнение Лиувилля обладает по сравнению с системой уравнений (8.4) двумя важными преимуществами. Во-первых, оно одно определяет поведение всей системы, а
во-вторых, позволяет наглядно и строго перейти к сокращенным уровням описания системы, в том числе к макроскопическому уровню. Такой переход мы подробно обсудим во второй части этой книги.
Оператор Лиувилля (11.2) не зависит явно от времени, поэтому решение начальной задачи для него имеет вид
 ,
,
 , (11.5)
, (11.5)
где мы ввели оператор  сдвига по траектории
сдвига по траектории  частиц. Если в некоторый момент времени фазовая координата частицы
частиц. Если в некоторый момент времени фазовая координата частицы  имела значение
имела значение  , то спустя время
, то спустя время 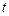 она станет равной
она станет равной 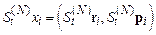 . Поэтому для произвольной функции
. Поэтому для произвольной функции 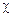 динамических переменных
динамических переменных  частиц имеем
частиц имеем
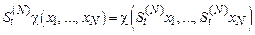 .
.
Таким образом, решение (11.5) можно представить в форме
 , (11.6)
, (11.6)
которая просто выражает свойство сохраняемости функции распределения системы вдоль динамической траектории, что, как мы уже отмечали, и является сутью теоремы Лиувилля.
Оператор эволюции определяется своим разложением в ряд Тейлора
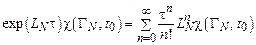 . (11.7)
. (11.7)
Он переводит систему из начального положения  в текущее
в текущее 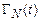 в момент времени
в момент времени  . Наоборот, оператор
. Наоборот, оператор  восстанавливает начальную функцию распределения
восстанавливает начальную функцию распределения 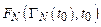 по текущей
по текущей
 .
.
Несмотря на то что мы называем выражение (11.5) решением уравнения Лиувилля и оно им является, записав его, мы не стали обладать большей информацией о системе. Связано это с тем, что формула (11.5) является просто формальной записью сложной эволюции системы за время  , которая сопровождается интенсивным
, которая сопровождается интенсивным  -частичным взаимодействием составляющих ее частиц. Поэтому, чтобы придать явный смысл решению (11.5) и оператору эволюции (11.7), следует решить соответствующую динамическую
-частичным взаимодействием составляющих ее частиц. Поэтому, чтобы придать явный смысл решению (11.5) и оператору эволюции (11.7), следует решить соответствующую динамическую  -частичную задачу. Как уже отмечалось, для системы большого числа частиц точное решение этой задачи бесперспективно. Однако, если нас интересует в каком-то смысле неполная информация о состоянии системы, то оператор эволюции (11.7) редуцируется к значительно более простому, явный вид которого можно определить. В сущности, построение таких редуцированных операторов для различных ситуаций и является задачей и неравновесной статистической механики, и кинетической теории.
-частичную задачу. Как уже отмечалось, для системы большого числа частиц точное решение этой задачи бесперспективно. Однако, если нас интересует в каком-то смысле неполная информация о состоянии системы, то оператор эволюции (11.7) редуцируется к значительно более простому, явный вид которого можно определить. В сущности, построение таких редуцированных операторов для различных ситуаций и является задачей и неравновесной статистической механики, и кинетической теории.



 ,
,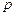 – давление среды;
– давление среды; 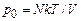 – давление идеального газа;
– давление идеального газа; 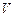 – объем системы, а также приведенной плотностью
– объем системы, а также приведенной плотностью  (напомним, что
(напомним, что  – диаметр молекулы).
– диаметр молекулы).
 , полученная методом молекулярной динамики, представлена на рис. 9.3. При исследованных плотностях наблюдается экспоненциальный рост давления с увеличением плотности системы.
, полученная методом молекулярной динамики, представлена на рис. 9.3. При исследованных плотностях наблюдается экспоненциальный рост давления с увеличением плотности системы.
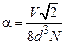 .
.
 ) и после перехода (
) и после перехода ( ). Время измеряется во временах свободного пробега молекул. В жидкости спустя малый начальный период времени зависимость близка к линейной. В твердом теле она ограничена размером зоны (вернее, его квадратом), в которой молекула может передвигаться. Для данной концентрации этот размер довольно велик – около трех диаметров молекулы. С ростом плотности размер этой зоны будет уменьшаться. Для сравнения: в реальном металле с силами молекулярного притяжения плавление начинается при смещении от узла кристаллической решетки атома примерно на 10 % его диаметра.
). Время измеряется во временах свободного пробега молекул. В жидкости спустя малый начальный период времени зависимость близка к линейной. В твердом теле она ограничена размером зоны (вернее, его квадратом), в которой молекула может передвигаться. Для данной концентрации этот размер довольно велик – около трех диаметров молекулы. С ростом плотности размер этой зоны будет уменьшаться. Для сравнения: в реальном металле с силами молекулярного притяжения плавление начинается при смещении от узла кристаллической решетки атома примерно на 10 % его диаметра.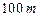 , но радиусы тяжелой и легких молекул одинаковы), то характер наблюдаемого фазового перехода практически не меняется. Коэффициент сжимаемости снова будет описываться сплошной кривой на рис. 9.4.
, но радиусы тяжелой и легких молекул одинаковы), то характер наблюдаемого фазового перехода практически не меняется. Коэффициент сжимаемости снова будет описываться сплошной кривой на рис. 9.4.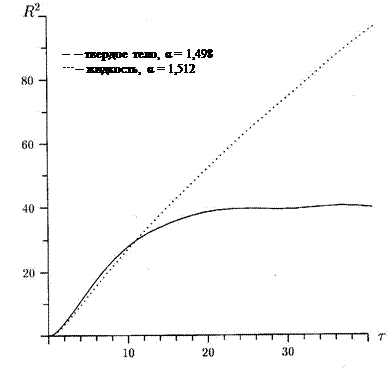
 , а отношение их радиусов – равным 4. Изотерме описанной гетерогенной системы (жидкость – наночастица) соответствует пунктирная кривая. В ячейке было 2637 молекул. Фазовый переход при наличии в системе дисперсной частицы происходит при бóльших плотностях и давлениях. Плотность, при которой имеет место фазовый переход, повышается. Коэффициент сжимаемости
, а отношение их радиусов – равным 4. Изотерме описанной гетерогенной системы (жидкость – наночастица) соответствует пунктирная кривая. В ячейке было 2637 молекул. Фазовый переход при наличии в системе дисперсной частицы происходит при бóльших плотностях и давлениях. Плотность, при которой имеет место фазовый переход, повышается. Коэффициент сжимаемости  при этом увеличивается с 11,9 до 12,95. Кроме того, в жидком состоянии давление в смеси меньше, чем в однофазной жидкости соответствующей плотности α. В самом деле, в жидком состоянии вся область около частицы доступна для молекул. Введение в однородную молекулярную жидкость дисперсной частицы приводит для несущей молекулярной среды к уменьшению доступного объема ячейки на величину объема частицы и, как следствие, – к уменьшению числа молекул. Значит, дисперсная система в жидком состоянии имеет более низкое давление, нежели однородная, что и показывает рис. 9.4 (правая ветвь изотермы при α > 1,43). Напротив, если смесь остается в твердом состоянии, около частицы образуются экранированные пустые области. Эффективный объем
при этом увеличивается с 11,9 до 12,95. Кроме того, в жидком состоянии давление в смеси меньше, чем в однофазной жидкости соответствующей плотности α. В самом деле, в жидком состоянии вся область около частицы доступна для молекул. Введение в однородную молекулярную жидкость дисперсной частицы приводит для несущей молекулярной среды к уменьшению доступного объема ячейки на величину объема частицы и, как следствие, – к уменьшению числа молекул. Значит, дисперсная система в жидком состоянии имеет более низкое давление, нежели однородная, что и показывает рис. 9.4 (правая ветвь изотермы при α > 1,43). Напротив, если смесь остается в твердом состоянии, около частицы образуются экранированные пустые области. Эффективный объем  частицы в твердом состоянии увеличивается.
частицы в твердом состоянии увеличивается.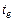 , то ошибки определения динамических переменных
, то ошибки определения динамических переменных 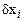 на таких временах должны быть малыми. Поскольку при использовании конечно-разностных схем того или иного порядка ошибка вычисления динамических переменных пропорциональна шагу дискретизации, этот шаг
на таких временах должны быть малыми. Поскольку при использовании конечно-разностных схем того или иного порядка ошибка вычисления динамических переменных пропорциональна шагу дискретизации, этот шаг  должен быть таким, чтобы выполнялось соотношение
должен быть таким, чтобы выполнялось соотношение  , где показатель
, где показатель  определяется порядком используемой схемы. На практике точность решения динамической задачи, как уже отмечалось, можно проверять по выполнению законов сохранения.
определяется порядком используемой схемы. На практике точность решения динамической задачи, как уже отмечалось, можно проверять по выполнению законов сохранения.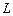 , появляется еще один источник ошибок. В реальном газе или жидкости возмущение, возникшее в некоторой точке, распространяется по всему объему и затем затухает из-за диссипативных эффектов. Размеры расчетной ячейки обычно достаточно малы, и возмущение, появившееся в некоторой точке, спустя время порядка
, появляется еще один источник ошибок. В реальном газе или жидкости возмущение, возникшее в некоторой точке, распространяется по всему объему и затем затухает из-за диссипативных эффектов. Размеры расчетной ячейки обычно достаточно малы, и возмущение, появившееся в некоторой точке, спустя время порядка  может вновь достичь ее. Здесь
может вновь достичь ее. Здесь 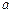 – скорость распространения возмущения, в газах и жидкостях – это скорость звука. Таким образом, гарантированную точность можно ожидать (при прочих равных условиях) лишь на временах порядка
– скорость распространения возмущения, в газах и жидкостях – это скорость звука. Таким образом, гарантированную точность можно ожидать (при прочих равных условиях) лишь на временах порядка 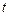 ~
~  в моделирующей системе становится источником серьезных ошибок в случае, когда моделируемая система большая (бесконечная). Физической причиной появления таких ошибок является то, что в конечной системе развиваются корреляции с характерными временами порядка времени изучения системы, не типичные для моделируемой системы. Корреляции эти в общем случае плохо изучены. Исключение представляет случай разреженного газа, который будет рассмотрен во второй части данного курса. Традиционный и самый простой способ проверки влияния конечного числа частиц на результаты расчета состоит в увеличении
в моделирующей системе становится источником серьезных ошибок в случае, когда моделируемая система большая (бесконечная). Физической причиной появления таких ошибок является то, что в конечной системе развиваются корреляции с характерными временами порядка времени изучения системы, не типичные для моделируемой системы. Корреляции эти в общем случае плохо изучены. Исключение представляет случай разреженного газа, который будет рассмотрен во второй части данного курса. Традиционный и самый простой способ проверки влияния конечного числа частиц на результаты расчета состоит в увеличении 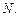 Именно поэтому изучение влияния эффекта конечных
Именно поэтому изучение влияния эффекта конечных  , где
, где 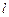 – средняя длина свободного пробега молекул газа. При нормальном давлении
– средняя длина свободного пробега молекул газа. При нормальном давлении 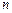 ~1019 молекул на кубический сантиметр. Поэтому число частиц, минимально необходимых для моделирования разреженного газа, порядка
~1019 молекул на кубический сантиметр. Поэтому число частиц, минимально необходимых для моделирования разреженного газа, порядка  . Поэтому точность, достижимая сегодня в обычных гидродинамических и теплофизических экспериментах, достигается уже при сравнительно небольшом числе частиц. Кроме того, конечность числа используемых в методе частиц стимулировала изучение поведения систем конечного числа частиц. Думается, что это самый перспективный метод их изучения. Связано это не только с технической сложностью экспериментального изучения явлений в системах малого числа частиц, хотя такие сложности, конечно, существуют. В некоторых случаях экспериментальное изучение принципиально ограничено, поскольку возмущения, вносимые прибором, оказываются порядка самого эффекта. Так обстоит дело, например, при изучении флуктуаций в малых объемах, которые очень важны, например, при исследовании процессов переноса наночастиц.
. Поэтому точность, достижимая сегодня в обычных гидродинамических и теплофизических экспериментах, достигается уже при сравнительно небольшом числе частиц. Кроме того, конечность числа используемых в методе частиц стимулировала изучение поведения систем конечного числа частиц. Думается, что это самый перспективный метод их изучения. Связано это не только с технической сложностью экспериментального изучения явлений в системах малого числа частиц, хотя такие сложности, конечно, существуют. В некоторых случаях экспериментальное изучение принципиально ограничено, поскольку возмущения, вносимые прибором, оказываются порядка самого эффекта. Так обстоит дело, например, при изучении флуктуаций в малых объемах, которые очень важны, например, при исследовании процессов переноса наночастиц.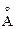 . Поэтому изучаемая система должна быть такой, чтобы данные масштабы были представительны. Использование периодических граничных условий предполагает, что свойства среды одинаковы с периодом, определяемым этими условиями. В твердом теле, где существует собственная периодическая структура, необходимо отслеживать влияние периодических граничных условий на реально существующую периодическую структуру.
. Поэтому изучаемая система должна быть такой, чтобы данные масштабы были представительны. Использование периодических граничных условий предполагает, что свойства среды одинаковы с периодом, определяемым этими условиями. В твердом теле, где существует собственная периодическая структура, необходимо отслеживать влияние периодических граничных условий на реально существующую периодическую структуру.
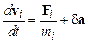 ,
,  (10.1)
(10.1)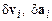 – стохастические составляющие скорости и ускорения частиц системы. Необратимость уравнений (10.1) позволяет вычислить по формулам типа Кубо коэффициенты переноса (коэффициента вязкости, диффузии и т.п.). В противном случае, если бы вычисляемые траектории частиц были обратимыми, соответствующие формулы давали нулевые значения, поскольку обратимое гамильтоново движение системы квазипериодично[32]. Как представляется, само существование коэффициентов переноса в природе является косвенным свидетельством в пользу того, что динамика системы должна описываться уравнениями типа (10.1).
– стохастические составляющие скорости и ускорения частиц системы. Необратимость уравнений (10.1) позволяет вычислить по формулам типа Кубо коэффициенты переноса (коэффициента вязкости, диффузии и т.п.). В противном случае, если бы вычисляемые траектории частиц были обратимыми, соответствующие формулы давали нулевые значения, поскольку обратимое гамильтоново движение системы квазипериодично[32]. Как представляется, само существование коэффициентов переноса в природе является косвенным свидетельством в пользу того, что динамика системы должна описываться уравнениями типа (10.1).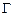 -пространстве вводится
-пространстве вводится 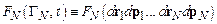 . Эта функция нормирована на единицу (см. соотношение (7.2)) и для системы тождественных частиц симметрична относительно перестановки их фазовых координат.
. Эта функция нормирована на единицу (см. соотношение (7.2)) и для системы тождественных частиц симметрична относительно перестановки их фазовых координат.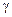 определяется числом представляющих точек в этом объеме и равна
определяется числом представляющих точек в этом объеме и равна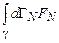 .
. . (11.1)
. (11.1)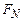 – функция времени и фазовых переменных,
– функция времени и фазовых переменных,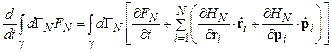 ,
, .
. .
.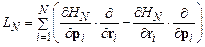 , (11.2)
, (11.2)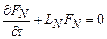 . (11.3)
. (11.3)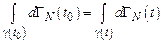 или
или 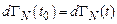 . (11.4)
. (11.4) в бесконечно малом объеме фазового пространства
в бесконечно малом объеме фазового пространства  равна
равна  . В момент же времени
. В момент же времени 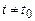 вероятность найти систему в объеме
вероятность найти систему в объеме 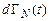 дается выражением
дается выражением ,
,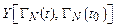 – якобиан преобразования от переменных
– якобиан преобразования от переменных 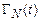 к –
к –  . В силу теоремы Лиувилля (11.4) якобиан
. В силу теоремы Лиувилля (11.4) якобиан 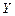 равен единице (это не сложно доказать и непосредственно, используя уравнения Гамильтона), а значит,
равен единице (это не сложно доказать и непосредственно, используя уравнения Гамильтона), а значит, 
 , т. е. функция распределения сохраняется вдоль траектории, а выражением этого факта и является уравнение Лиувилля (11.3).
, т. е. функция распределения сохраняется вдоль траектории, а выражением этого факта и является уравнение Лиувилля (11.3). ,
, , (11.5)
, (11.5) сдвига по траектории
сдвига по траектории  имела значение
имела значение  , то спустя время
, то спустя время 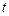 она станет равной
она станет равной 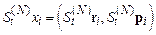 . Поэтому для произвольной функции
. Поэтому для произвольной функции 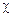 динамических переменных
динамических переменных 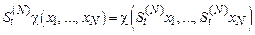 .
. , (11.6)
, (11.6)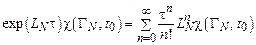 . (11.7)
. (11.7) . Наоборот, оператор
. Наоборот, оператор  восстанавливает начальную функцию распределения
восстанавливает начальную функцию распределения 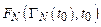 по текущей
по текущей .
. , которая сопровождается интенсивным
, которая сопровождается интенсивным 

