Метод молекулярной динамики
Прямое численное моделирование различных явлений и процессов является самым современным и мощным средством их исследования. Нередко его предпочитают эксперименту, поскольку экспериментальное изучение обычно значительно дороже[27], а в некоторых случаях, как происходит, например, при изучении ряда свойств наночастиц[28], просто невозможно. Использование того или иного метода моделирования определяется многими обстоятельствами и прежде всего характером самой изучаемой системы и степенью подробности необходимой информации. Системой мы называем произвольную совокупность взаимодействующих между собой и с окружением элементов. Часто мы говорим о системе частиц. В принципе в качестве «частиц» опять можно рассматривать произвольные элементы. В простейшем случае это может быть система физических частиц, элементарных частиц (протонов, нейтронов, электронов и т.п.), атомов, молекул, кристаллов, кластеров, дисперсных частиц. Если законы взаимодействия этих частиц известны, то динамика такой системы многих частиц будет описываться системой уравнений Ньютона (5.3) (или соответствующих квантово-механических уравнений). В результате решения этой системы уравнений мы получаем полный набор динамических переменных системы (координат и скоростей), и такое описание принято называть микроскопическим, поскольку оно является наиболее подробным из всех возможных (см. разд. 7).
Систему многих частиц представляет собой газ, жидкость, плазма, твердое тело, различные гетерогенные системы, газовзвеси, суспензии, эмульсии, гранулированные среды (типичными представителями последних являются песок и зерно). Системой многих частиц являются планетные и звездные системы. С системами многих частиц мы сталкиваемся в различных технологических устройствах: химических реакторах, зерносушилках, доменных печах и конверторах, двигателях внутреннего сгорания, ракетных двигателях. Конечно, этот перечень легко продолжить.
В данном разделе мы рассмотрим метод прямого численного моделирования различных систем многих частиц, описываемых уравнениями Ньютона. Если система состоит из большого числа частиц (фактически, если число частиц больше двух), то единственным непосредственным способом описания системы на микроскопическом уровне сегодня является моделирование движения составляющих систему частиц с помощью компьютера. Такой метод изучения эволюции системы большого числа частиц называется методом молекулярной динамики. Описанию этого метода и будет посвящен настоящий раздел.
Метод молекулярной динамики
Исходным пунктом метода молекулярной динамики является система уравнений Ньютона (5.3а) для рассматриваемой системы частиц. Определяющим элементом подобного микроскопического моделирования эволюции системы будет задание межчастичных сил. На практике используются обычно либо непрерывные потенциалы типа потенциала Леннарда – Джонса
 , (9.1)
, (9.1)
либо потенциал твердых сфер
 (9.2)
(9.2)
здесь  – эффективный размер сферы, которой моделируется частица;
– эффективный размер сферы, которой моделируется частица; 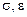 – параметры потенциала Леннарда – Джонса.
– параметры потенциала Леннарда – Джонса.
При надлежащем выборе указанных параметров с помощью потенциалов (9.1), (9.2) удается описать самые разные свойства систем: от законов рассеяния частиц при их соударении до термодинамических и переносных свойств системы, включая, например, давление, температуру, плотность, коэффициенты вязкости, теплопроводности, диффузии и т. д. Реализация метода в этих двух случаях различна. Ниже будут рассмотрены принципиальные схемы построения алгоритмов для обеих ситуаций.
Непрерывные потенциалы
Обычно при использовании метода молекулярной динамики потенциалы межмолекулярного взаимодействия предполагаются парными и аддитивными[29]. Динамика системы описывается тогда системой уравнений Ньютона (5.3a)
 (9.3)
(9.3)
и задача состоит в решении данной системы уравнений на компьютере. Для этого выбирается ячейка, чаще всего кубическая, в которую помещаются от нескольких сотен до нескольких тысяч частиц. Каждой частице по некоторому закону приписывают начальную скорость. Дальше для системы уравнений (9.3) необходимо решить задачу Коши определения координат и импульсов всех частиц в некоторый момент времени, если эти данные были известны в предыдущий. С этой целью уравнения (9.3) заменяются конечно-разностными. Для молекулы  по известным динамическим переменным в момент
по известным динамическим переменным в момент 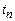 мы должны определить их значения в момент
мы должны определить их значения в момент  Разработано много различных алгоритмов вычисления рассматриваемых динамических переменных. Простейшая дискретизация уравнений (9.3) имеет вид
Разработано много различных алгоритмов вычисления рассматриваемых динамических переменных. Простейшая дискретизация уравнений (9.3) имеет вид
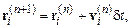
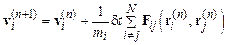 . (9.4)
. (9.4)
Эта схема явная, первого порядка точности по 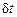 и носит название схемы Эйлера. Существуют и более сложные аппроксимации. В методе центральных разностей принимается, что приращения координат определяются значениями скоростей на середине временного шага:
и носит название схемы Эйлера. Существуют и более сложные аппроксимации. В методе центральных разностей принимается, что приращения координат определяются значениями скоростей на середине временного шага:

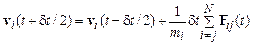 . (9.5)
. (9.5)
Многие алгоритмы используют разложение функции 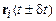 в ряд Тейлора
в ряд Тейлора
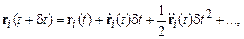
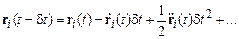 (9.6)
(9.6)
Сложение этих двух уравнений с точностью до членов третьего порядка включительно дает
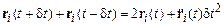 . (9.7)
. (9.7)
Скорость получается вычитанием этих двух уравнений. С той же точностью имеем
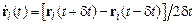 . (9.8)
. (9.8)
В результате
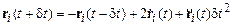 . (9.9)
. (9.9)
Описанный алгоритм был предложен Л. Верле. Использовались и многочисленные иные схемы. Применяются, например, схема предиктор – корректор, методы Рунге – Кутта различного порядка точности и т.д. Вообще выбор численной аппроксимации в значительной мере диктуется решаемой задачей и в каждом конкретном случае должен обсуждаться особо. Интервал 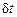 следует выбирать так, чтобы процедура интегрирования системы уравнений (9.3) была устойчива и давала решение, отклонение которого от точного как можно медленнее росло бы со временем. Устойчивость решения контролируется обычно по выполнению законов сохранения.
следует выбирать так, чтобы процедура интегрирования системы уравнений (9.3) была устойчива и давала решение, отклонение которого от точного как можно медленнее росло бы со временем. Устойчивость решения контролируется обычно по выполнению законов сохранения.
Все координаты, скорости и ускорения частиц, вычисляемые в различные моменты времени, заносятся в память машины и могут затем использоваться для расчета тех или иных свойств системы. Расчеты многократно повторяются, что приводит к созданию ансамбля различных реализаций эволюции исследуемой системы в фазовом пространстве.
Твердые гладкие сферы
Для системы, молекулы которой моделируются упругими твердыми сферами, схема применения метода молекулярной динамики существенно упрощается. Здесь нам вообще не приходится решать систему уравнений Ньютона. В этом случае вся процедура сводится к нахождению в системе последовательности времен между столкновениями молекул и определению из этого ряда на каждом шаге минимального времени, которое и задает реально столкнувшуюся пару молекул. Затем все частицы сдвигаются вдоль своих траекторий на это минимальное время, а скорости столкнувшихся частиц пересчитываются. Далее процедура расчета повторяется. Этот метод был предложен Б. Олдером[30] и
Т. Вайнрайтом и впоследствии многократно модифицировался.
Рассмотрим подробнее, как определяется время до столкновения двух частиц. Итак, пусть даны две частицы, имеющие скорости 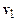 и
и 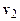 и находящиеся в начальный момент времени в точках с координатами
и находящиеся в начальный момент времени в точках с координатами 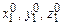 и
и 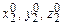 . Будем считать, что их столкновение произошло через время
. Будем считать, что их столкновение произошло через время 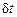 . При этом координаты частиц приняли значения
. При этом координаты частиц приняли значения 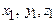 и
и 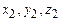 соответственно. В момент столкновения выполняется условие
соответственно. В момент столкновения выполняется условие
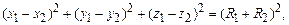 (9.10)
(9.10)
где 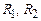 – радиусы твердых сфер. В течение времени
– радиусы твердых сфер. В течение времени 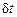 (до столкновения) частицы двигались с постоянными скоростями
(до столкновения) частицы двигались с постоянными скоростями 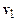 и
и 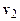 , поэтому
, поэтому
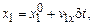
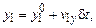

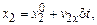
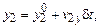
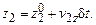
Тогда для определения времени до столкновения получается квадратное уравнение
 , (9.11)
, (9.11)
где
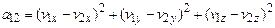 ;
;
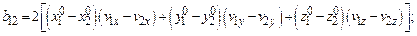
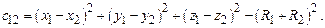
Вещественные корни этого уравнения существуют, если
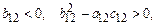
и в этом случае равны
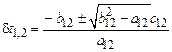 .
.
Необходимо выбрать минимальный корень, поскольку именно он соответствует столкновению. Второй корень отвечает выполнению условия (9.10) при прохождении одной частицы «сквозь» другую. Если условия (9.11) не выполняются, то столкновения нет и 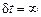 .
.
После того как столкновение двух частиц произошло, необходимо пересчитать их скорости. Для этого используются законы сохранения импульса и энергии
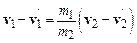 ,
,
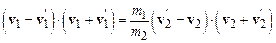 . (9.12)
. (9.12)
Знаком штрих обозначены скорости частиц после столкновения.
Введем единичные векторы: 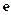 – направленный по нормали к поверхностям сталкивающихся твердых сфер от первой частицы ко второй, и
– направленный по нормали к поверхностям сталкивающихся твердых сфер от первой частицы ко второй, и 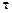 – касательный к этим поверхностям. Переписав законы соударения частиц (9.12), получаем их скорости после столкновения
– касательный к этим поверхностям. Переписав законы соударения частиц (9.12), получаем их скорости после столкновения
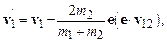
 (9.13)
(9.13)
Вектор 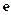 определяется из соотношения
определяется из соотношения
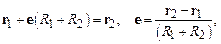
где 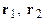 – радиусы-векторы центров сталкивающихся сфер.
– радиусы-векторы центров сталкивающихся сфер.



 , (9.1)
, (9.1) (9.2)
(9.2) – эффективный размер сферы, которой моделируется частица;
– эффективный размер сферы, которой моделируется частица; 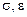 – параметры потенциала Леннарда – Джонса.
– параметры потенциала Леннарда – Джонса.  (9.3)
(9.3) по известным динамическим переменным в момент
по известным динамическим переменным в момент 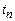 мы должны определить их значения в момент
мы должны определить их значения в момент  Разработано много различных алгоритмов вычисления рассматриваемых динамических переменных. Простейшая дискретизация уравнений (9.3) имеет вид
Разработано много различных алгоритмов вычисления рассматриваемых динамических переменных. Простейшая дискретизация уравнений (9.3) имеет вид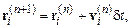
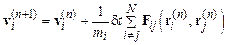 . (9.4)
. (9.4)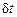 и носит название схемы Эйлера. Существуют и более сложные аппроксимации. В методе центральных разностей принимается, что приращения координат определяются значениями скоростей на середине временного шага:
и носит название схемы Эйлера. Существуют и более сложные аппроксимации. В методе центральных разностей принимается, что приращения координат определяются значениями скоростей на середине временного шага:
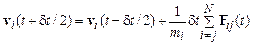 . (9.5)
. (9.5)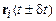 в ряд Тейлора
в ряд Тейлора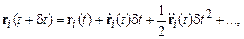
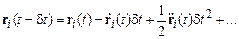 (9.6)
(9.6)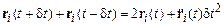 . (9.7)
. (9.7)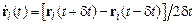 . (9.8)
. (9.8)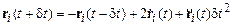 . (9.9)
. (9.9)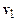 и
и 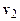 и находящиеся в начальный момент времени в точках с координатами
и находящиеся в начальный момент времени в точках с координатами 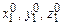 и
и 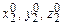 . Будем считать, что их столкновение произошло через время
. Будем считать, что их столкновение произошло через время 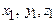 и
и 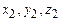 соответственно. В момент столкновения выполняется условие
соответственно. В момент столкновения выполняется условие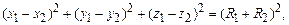 (9.10)
(9.10)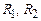 – радиусы твердых сфер. В течение времени
– радиусы твердых сфер. В течение времени 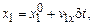
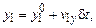

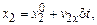
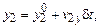
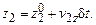
 , (9.11)
, (9.11)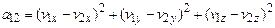 ;
;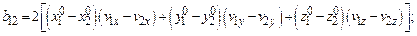
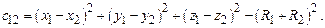
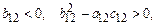
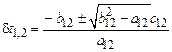 .
.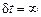 .
.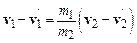 ,
,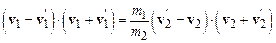 . (9.12)
. (9.12)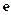 – направленный по нормали к поверхностям сталкивающихся твердых сфер от первой частицы ко второй, и
– направленный по нормали к поверхностям сталкивающихся твердых сфер от первой частицы ко второй, и 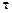 – касательный к этим поверхностям. Переписав законы соударения частиц (9.12), получаем их скорости после столкновения
– касательный к этим поверхностям. Переписав законы соударения частиц (9.12), получаем их скорости после столкновения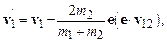
 (9.13)
(9.13)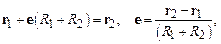
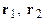 – радиусы-векторы центров сталкивающихся сфер.
– радиусы-векторы центров сталкивающихся сфер.


