Метод последовательных приближений, использованный выше, справедлив при условии отсутствия линейного резонанса, в противном случае решение (3.17) расходится. Что же произойдет, если на нелинейный осциллятор действует вынуждающая сила с частотой, равной собственной частоте соответствующего линейного осциллятора? Пусть, скажем, имеется осциллятор с кубической нелинейностью
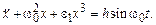 (3.18)
(3.18)
В отсутствие нелинейного члена (e1 = 0) мы имеем обычный случай линейного резонанса (решение (2.14)), амплитуда колебаний неограниченно растет со временем. Иначе дело обстоит с нелинейным осциллятором (3.18). Мы установили, что частота колебаний нелинейного осциллятора зависит от амплитуды колебаний (см. формулу (3.15)):
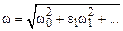
В частности, раскладывая это выражение в ряд по малому параметру e1, с учетом (3.14) в первом приближении имеем
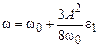 . (3.19)
. (3.19)
Будем искать теперь решение уравнения (3.18) в виде ряда

Тогда в нулевом приближении по параметру e1 приходим к уравнению
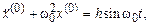
решение которого при однородных начальных условиях имеет вид
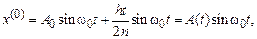 (3.20)
(3.20)
где  – амплитуда резонансных колебаний, a
– амплитуда резонансных колебаний, a 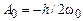 . Решение (3.20) показывает, что эффективная амплитуда колебаний
. Решение (3.20) показывает, что эффективная амплитуда колебаний 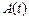 растет со временем. Вспоминая (3.19), мы видим, что частота колебаний рассматриваемого осциллятора (3.18) меняется со временем. На малых временах w(t) она мало отличается от w0, так как e1 << 1, и условия резонанса выполняются, амплитуда колебаний растет. Однако с ростом t частота колебаний осциллятора все больше и больше отличается от частоты вынуждающей силы w0 (и собственной частоты линейного осциллятора!). Вынуждающая сила перестает быть резонансной. Система выходит из резонанса, амплитуда колебаний перестает нарастать. Таким образом, наличие нелинейности в уравнении осциллятора приводит лишь к ограниченному росту амплитуды колебаний в условиях существования линейного резонанса.
растет со временем. Вспоминая (3.19), мы видим, что частота колебаний рассматриваемого осциллятора (3.18) меняется со временем. На малых временах w(t) она мало отличается от w0, так как e1 << 1, и условия резонанса выполняются, амплитуда колебаний растет. Однако с ростом t частота колебаний осциллятора все больше и больше отличается от частоты вынуждающей силы w0 (и собственной частоты линейного осциллятора!). Вынуждающая сила перестает быть резонансной. Система выходит из резонанса, амплитуда колебаний перестает нарастать. Таким образом, наличие нелинейности в уравнении осциллятора приводит лишь к ограниченному росту амплитуды колебаний в условиях существования линейного резонанса.
Субгармонический резонанс
Итак, в нелинейных системах амплитуды колебаний ограничены (конечны), даже если частота вынужденных колебаний совпадает с собственной частотой соответствующего линейного осциллятора. С другой стороны, в нелинейных системах возможны иные типы резонансов. Изучив особенности эволюции нелинейного осциллятора, мы могли бы теперь предсказать, в каких случаях в такой осцилляторной системе реализуются резонансные явления.
Действительно, характерная черта нелинейной колебательной системы – появление комбинационных частот – супергармоник. Для осциллятора с квадратичной нелинейностью (3.16) первой появляется комбинационная частота, равная удвоенной собственной частоте осциллятора и удвоенной частоте внешней силы (3.17). Поэтому, если на такой осциллятор действует сила с частотой, равной половине собственной частоты линейного осциллятора f 1sin(w0 t /2), то в системе обязательно возникнет комбинационная частота w0, которая и является резонансной. Частоты
w i = w0/ i, где i = 2, 3,..., называются субгармониками, а резонанс, обусловленный действием на систему гармонической силы на субгармонической частоте, – субгармоническим резонансом.
Параметрический резонанс
Другой тип резонанса, который может возникнуть в нелинейных системах, связан с появлением в линейных уравнениях периодических во времени коэффициентов. Рассмотрим сначала линейный осциллятор с периодически изменяющейся частотой
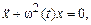 (3.21)
(3.21)
где 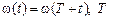 – период колебаний.
– период колебаний.
Выясним условия возникновения резонанса в важном случае, когда функция w(t) мало отличается от некоторой постоянной величины w0 и является простейшей периодической функцией

где h << 1.
Уравнение (3.21) тогда принимает вид

или
 (3.21а)
(3.21а)
Учитывая, что h << 1, будем искать решение последнего уравнения в виде ряда по малому параметру h
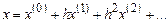 (3.22)
(3.22)
Подставляя это решение в уравнение (3.21а), для функций x (i) получаем следующую систему уравнений:
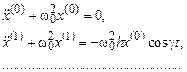 (3.22a)
(3.22a)
С учетом того, что  второе уравнение системы принимает вид
второе уравнение системы принимает вид

(3.23)

Правая часть уравнения (3.23) показывает, что условием возникновения резонанса является соотношение
 (3.24)
(3.24)
Таким образом, изменение частоты колебаний линейного осциллятора по гармоническому закону с частотой, равной удвоенной собственной частоте, будет приводить к резонансу.
Теперь покажем, как в нелинейной системе может возникнуть параметрический резонанс. Пусть вынуждающая сила в (3.16) имеет вид 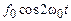 . Не нарушая общности, будем искать решение в виде
. Не нарушая общности, будем искать решение в виде 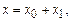 где
где 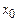 – частное решение линейной
– частное решение линейной
задачи:
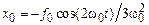 .
.
После подстановки 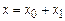 в (3.16) получим
в (3.16) получим
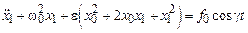 .
.
Таким образом, мы пришли к нелинейному уравнению относительно х 1. Пусть e << 1, ½ f 0½<< 1. Тогда, ограничиваясь только линейными членами, приходим к неоднородному уравнению
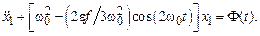
Это уравнение подобно однородному уравнению (3.23). Следовательно, за счет нелинейности мы приходим к эквивалентной линейной системе, параметры которой периодически зависят от времени. В случае вынуждающей силы с частотой g = 2w0 и наблюдается явление параметрического резонанса.
Возможность появления резонанса под воздействием силы с удвоенной частотой свободных линейных колебаний можно установить непосредственно из уравнения (3.17). Из него следует, что условием резонанса является равенство  или
или  . При необходимости можно доказать, что резонанс возможен как субгармонический при g = w0/ n, так и параметрический при g = m w0, где m, n – целые числа.
. При необходимости можно доказать, что резонанс возможен как субгармонический при g = w0/ n, так и параметрический при g = m w0, где m, n – целые числа.



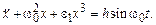 (3.18)
(3.18)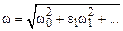
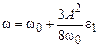 . (3.19)
. (3.19)
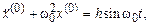
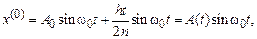 (3.20)
(3.20) – амплитуда резонансных колебаний, a
– амплитуда резонансных колебаний, a 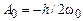 . Решение (3.20) показывает, что эффективная амплитуда колебаний
. Решение (3.20) показывает, что эффективная амплитуда колебаний 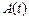 растет со временем. Вспоминая (3.19), мы видим, что частота колебаний рассматриваемого осциллятора (3.18) меняется со временем. На малых временах w(t) она мало отличается от w0, так как e1 << 1, и условия резонанса выполняются, амплитуда колебаний растет. Однако с ростом t частота колебаний осциллятора все больше и больше отличается от частоты вынуждающей силы w0 (и собственной частоты линейного осциллятора!). Вынуждающая сила перестает быть резонансной. Система выходит из резонанса, амплитуда колебаний перестает нарастать. Таким образом, наличие нелинейности в уравнении осциллятора приводит лишь к ограниченному росту амплитуды колебаний в условиях существования линейного резонанса.
растет со временем. Вспоминая (3.19), мы видим, что частота колебаний рассматриваемого осциллятора (3.18) меняется со временем. На малых временах w(t) она мало отличается от w0, так как e1 << 1, и условия резонанса выполняются, амплитуда колебаний растет. Однако с ростом t частота колебаний осциллятора все больше и больше отличается от частоты вынуждающей силы w0 (и собственной частоты линейного осциллятора!). Вынуждающая сила перестает быть резонансной. Система выходит из резонанса, амплитуда колебаний перестает нарастать. Таким образом, наличие нелинейности в уравнении осциллятора приводит лишь к ограниченному росту амплитуды колебаний в условиях существования линейного резонанса.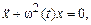 (3.21)
(3.21)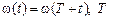 – период колебаний.
– период колебаний.

 (3.21а)
(3.21а)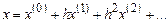 (3.22)
(3.22)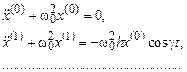 (3.22a)
(3.22a) второе уравнение системы принимает вид
второе уравнение системы принимает вид

 (3.24)
(3.24)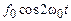 . Не нарушая общности, будем искать решение в виде
. Не нарушая общности, будем искать решение в виде 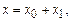 где
где 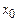 – частное решение линейной
– частное решение линейной 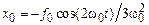 .
.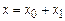 в (3.16) получим
в (3.16) получим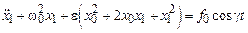 .
.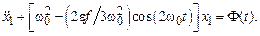
 или
или  . При необходимости можно доказать, что резонанс возможен как субгармонический при g = w0/ n, так и параметрический при g = m w0, где m, n – целые числа.
. При необходимости можно доказать, что резонанс возможен как субгармонический при g = w0/ n, так и параметрический при g = m w0, где m, n – целые числа.


