Локальная неустойчивость и перемешивание

 

Суть задачи теории устойчивости сводится к ответу на вопрос: как изменится фазовая траектория системы при малом изменении тех или иных ее параметров. Можно сформулировать очень много различных задач устойчивости. Все зависит от того, какие параметры системы будут варьироваться. Например, в случае системы многих частиц можно изменить силы, действующие между частицами, или их массы, или начальные скорости, или начальные координаты и т.д. Ясно, что система может быть устойчива к изменению одних параметров, но не устойчива по отношению к изменению других. Поэтому прежде чем поставить задачу устойчивости, надо договориться, относительно вариации каких параметров будет идти речь. В настоящем разделе мы будем рассматривать только одну, но зато наиболее распространенную задачу устойчивости – задачу об изучении устойчивости системы относительно малых изменений начальных данных. Несмотря на то что задача эта частная, полученный результат оказывается достаточно универсальным. Методы, развитые при решении этой конкретной задачи, применимы и при решении задач устойчивости относительно вариации других параметров системы.

Итак, пусть динамическая система описывается уравнениями (5.2), а начальные условия имеют вид (5.2а). Решение соответствующей задачи Коши имеет вид

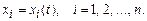                          (5.6)

Движение системы в фазовом пространстве, описываемое функциями (5.6), называется невозмущенным движением.

Пусть далее  – решение системы (5.2), удовлетворяющее измененным начальным условиям

                        (5.7)

Движение системы, отвечающее этим начальным условиям, называется возмущенным движением.

Введенные понятия невозмущенного и возмущенного движений проиллюстрированы на рис. 5.1. Здесь показаны невозмущенное движение 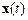, соответствующее начальным условиям (5.2а), и два возмущенных движения  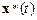и 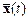 с иными начальными данными. Какое же движение системы (5.2) будет устойчивым, а какое неустойчивым? В ответе на этот вопрос мы будем следовать определению, данному А.М. Ляпуновым[13].

 

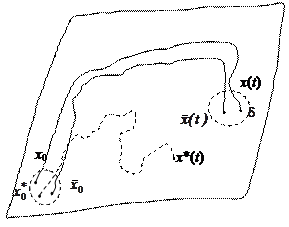Рис. 5.1.  Устойчивая по Ляпунову  и неус-

тойчивая 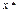траектории в фазовом простран-

стве системы

 

 

Определение. Решение 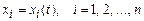, удовлетворяющее уравнениям (5.2) и начальным условиям (5.2а), называется устойчивым по Ляпунову, если для каждого как угодно малого  можно указать  такое, что при всех значениях  будут выполняться неравенства

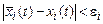,                             (5.8)

если начальные данные удовлетворяют неравенствам .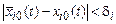

Разности между значениями возмущенного и невозмущенного движений

,

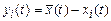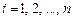
называются возмущениями или вариациями величин 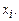 Если все отклонения равны нулю, т. е. , то возмущенное движение будет совпадать с невозмущенным движением. На рис. 5.1 показаны невозмущенная траектория движения некоторой системы 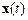 и две возмущенные траектории движения  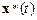и 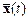. Первая из них по Ляпунову определяет устойчивое движение, а вторая – неустойчивое.

В настоящее время разработано несколько конструктивных методов изучения устойчивости решений динамических систем, основу которых заложил еще А.М. Ляпунов. Рассмотрение этих методов, однако, выходит за рамки данного пособия, с ними можно познакомиться в специальной литературе[14]. Здесь лишь подчеркнем, что для систем многих взаимодействующих частиц, которые являются моделями самых разных процессов и явлений[15], фазовые траектории почти всегда оказываются неустойчивыми. Формально это означает, что расстояние между двумя фазовыми траекториями растет со временем

,

где 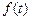 – некоторая растущая функция времени. Если эта функция экспоненциальная

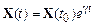,                         (5.9)

то такой тип неустойчивости движения системы называется локальной неустойчивостью, а 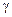 – инкрементом неустойчивости. Согласно (5.9) разбегание фазовых траекторий происходит экспоненциально. Движение в фазовом пространстве системы многих взаимодействующих частиц характеризуется именно этим свойством, т. е. имеет место локальная неустойчивость их траекторий. Однако можно сформулировать еще более сильное утверждение. Для этого рассмотрим две произвольные функции динамических переменных –  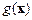и 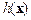. Это могут быть, например, импульс системы и ее энергия. Среднее значение этих величин по фазовому пространству  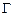определяется так:

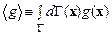.                         (5.10)

Оказывается, что локальная неустойчивость для широкого круга интересных с практической точки зрения динамических систем сопровождается и свойством перемешивания, поэтому временная корреляционная функция некоторых двух динамических переменных с течением времени затухает. Как принято говорить, в статистической физике имеет место затухание корреляций.

Корреляционную функцию величин 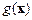 и 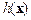 будем обозначать , и она равна

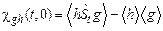,                       (5.11)

где 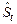 – динамический оператор эволюции системы, он переводит динамические переменные всех частиц системы из некоторого начального момента времени в положение, определяемое моментом времени t:

                               (5.12)

Таким образом, этот оператор осуществляет сдвиг всех переменных системы вдоль фазовой траектории на время 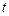. Конструктивное определение этого оператора для различных динамических переменных будет дано позднее.

С учетом определения (5.11) условие перемешивания можно записать так:

                            (5.13)

Отсутствие корреляций означает, как известно, статистическую независимость рассматриваемых динамических величин. Если сделать еще один шаг в указанном направлении, то можно сказать, что условие (5.13) асимптотически (в указанном пределе) устанавливает стохастическое поведение данных динамических величин. Динамическая система родила еще один очень важный мотив. Оказывается, что определяемые ею динамические величины могут вести себя в известном смысле стохастически.

Объем фазового пространства, занимаемый механической системой  упруго взаимодействующих частиц[16], с течением времени сохраняется (это утверждение называется теоремой Лиувилля, см. ч. II), однако форма его с течением времени очень сильно меняется и принимает весьма причудливую форму. В своей замечательной монографии Дж. Гиббс иллюстрирует свойство перемешивания на примере чернильной капли, которую роняют в воду. Ее объем с течением времени не меняется, однако капля все более и более равномерно растягивается, окрашивая всю жидкость.

Для систем, в которых имеет место локальная неустойчивость (5.9), для свойства перемешивания можно установить оценку

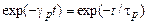 ~ ,               (5.14)

где время 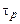 – время расцепления корреляций, т. е. время, на котором корреляции уменьшаются в  раз.

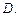За счет чего происходит перемешивание в реальных динамических системах? Чтобы разобраться в этом, рассмотрим простую модель двухкомпонентной среды. Будем считать, что среда состоит из молекул, диаметр которых  и частиц диаметром  Те и другие будем моделировать абсолютно упругими сферами.

 

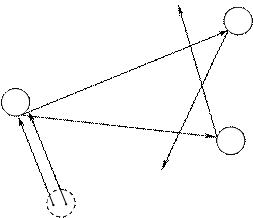Рис. 5.2. Картина рассеивания крупными частицами

двух молекул, стартующих из близких положений

 

 

кроме того, пусть  Картина рассеивания двух молекул, стартующих из близкой окрестности некоторой точки 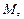 показана на рис 5.2. Здесь траектории молекул показаны стрелками, а частицы – белыми кружками. Видно, что уже через два столкновения траектории молекул в пространстве разошлись очень значительно. И чем больше соударений с частицами произойдет, тем эти различия будут существеннее. Ясно, что в фазовом пространстве, где проявляется различие не только в конфигурациях частиц (их положении в физическом пространстве), но и в скоростях, это разбегание будет происходить еще быстрее.