2.1. Несколько примеров колебательных систем
Колебательные процессы – одни из самых распространенных и в природных условиях, и в различных технических установках. Вся наша жизнь характеризуется постоянной круговертью дня и ночи, лета и зимы, рождения и смерти. Сердце должно сократиться 60 раз в минуту, чтобы обеспечить наш организм живительной силой крови и кислорода. Всякое нарушение этого ритма – тревожный признак. Сегодня, наверное, трудно найти техническое устройство или живой организм, в которых не наблюдались бы те или иные периодические явления или процессы. Все они описываются очень похожими математическими моделями. Прежде чем сформулировать эти модели, рассмотрим несколько примеров колебательных систем.
Колебательная система, возникающая
При действии упругой силы
Рассмотрим механическую систему с одной степенью свободы. В частности, это может быть материальная точка. Пусть на материальную точку действует сила  , являющаяся функцией координаты
, являющаяся функцией координаты  , т. е. зависящая от положения точки относительно начала координат
, т. е. зависящая от положения точки относительно начала координат
 . (2.1)
. (2.1)
Уравнением типа (2.1) описывается динамика самых разных физических систем: движение атомов кристаллической решетки, изменение заряда в колебательном контуре, движение в поле тяжести и т.д. Для широкого класса функций F силу можно представить в виде степенного ряда
 (2.2)
(2.2)
где F (0) – некоторая постоянная сила, действующая на материальную точку в начале координат. Часто эту силу можно считать равной нулю. Тогда, если в разложении (2.2)  , где с > 0, а
, где с > 0, а 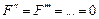 , мы приходим к уравнению линейного осциллятора
, мы приходим к уравнению линейного осциллятора
 , (2.3)
, (2.3)
а в случае, когда старшие производные функции F отличны от нуля, – к уравнению нелинейного осциллятора
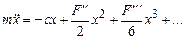 (2.4)
(2.4)
Сохраняя в этом уравнении первые два члена, получим осциллятор с квадратичной нелинейностью. Если отличны от нуля лишь первый и третий члены в правой части уравнения (2.4), получается осциллятор с кубической нелинейностью и т.д.
Нелинейное уравнение (2.4) описывает самые разные колебательные процессы, происходящие в природе. Рассмотрим два типичных примера. Первым является движение груза (материальной точки) массы m, подвешенного на пружине (рис. 2.1). Начало координат на рис. 2.1 выбрано в положении равновесия груза. При отклонении груза от положения равновесия на x на него со стороны пружины действует упругая восстанавливающая сила F (x). Если 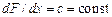 , пружину называют линейной
, пружину называют линейной
(рис. 2.2, прямая 1). Восстанавливающая сила пропорциональна отклонению груза от положения равновесия x лишь при малых отклонениях, когда справедлив закон Гука. При больших отклонениях закон Гука перестает выполняться, и мы имеем «нелинейную» пружину. Ее называют жесткой, когда сила ½ F (x)½ растет с ½ x ½ быстрее, чем для линейной пружины (рис. 2.2, кривая 2) и мягкой, если ½ F (x)½ растет с ½ x ½ медленнее, чем в случае выполнения закона Гука (кривая 3).
Рис. 2.1. Модель Рис. 2.2. Зависимость жесткости
простейшего пружины от величины ее
осциллятора удлинения
Математический маятник
В качестве второго примера рассмотрим движение математического маятника в поле тяжести (рис. 2.3). Материальная точка m, подвешенная на нерастяжимой нити l, имеет одну степень свободы, описываемую углом отклонения j нити от положения равновесия. Уравнение движения груза имеет вид
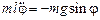 . (2.5)
. (2.5)
Раскладывая sin j в ряд Тейлора вблизи равновесия, имеем
 (2.6)
(2.6)
Таким образом, малые колебания математического маятника описываются уравнением линейного осциллятора
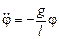 , (2.7)
, (2.7)
а при конечных отклонениях груза от положения равновесия мы имеем нелинейный осциллятор с кубической нелинейностью. Так как 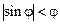 , ясно, что математический маятник соответствует
, ясно, что математический маятник соответствует
Рис. 2.3. Математический
маятник
случаю мягкой пружины. В случае, когда на осциллятор действует сила трения, пропорциональная скорости, его уравнение принимает вид
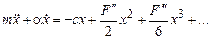 (2.8)
(2.8)
Здесь a – некоторый коэффициент трения.



 , являющаяся функцией координаты
, являющаяся функцией координаты  , т. е. зависящая от положения точки относительно начала координат
, т. е. зависящая от положения точки относительно начала координат . (2.1)
. (2.1) (2.2)
(2.2) , где с > 0, а
, где с > 0, а 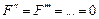 , мы приходим к уравнению линейного осциллятора
, мы приходим к уравнению линейного осциллятора , (2.3)
, (2.3)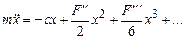 (2.4)
(2.4)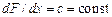 , пружину называют линейной
, пружину называют линейной 
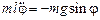 . (2.5)
. (2.5) (2.6)
(2.6)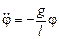 , (2.7)
, (2.7)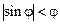 , ясно, что математический маятник соответствует
, ясно, что математический маятник соответствует
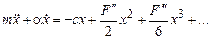 (2.8)
(2.8)


