Электрический колебательный контур также хорошо известен (рис. 2.4). Он состоит из катушки индуктивности 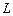 и конденсатора
и конденсатора  соединенных между собой проводниками. Если разность потенциалов на пластинах конденсатора в момент времени
соединенных между собой проводниками. Если разность потенциалов на пластинах конденсатора в момент времени 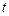 равна
равна 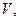 то заряд конденсатора
то заряд конденсатора  Если емкость конденсатора постоянна, то уравнение движения заряда в цепи – это уравнение линейного осциллятора
Если емкость конденсатора постоянна, то уравнение движения заряда в цепи – это уравнение линейного осциллятора
 . (2.9)
. (2.9)
Рис. 2.4. Схема колебательного
контура
В общем случае емкость конденсатора зависит от величины находящегося в нем заряда. Соответствующее уравнение движения заряда будет уже нелинейным.
Простая модель динамики популяции
Рассмотрим теперь совершенно экзотическую задачу о динамике двух взаимосвязанных видов животных: хищников  и их жертв
и их жертв  . В отсутствие хищников рост последних обусловлен наличием соответствующих условий и пропорционален их числу[4]
. В отсутствие хищников рост последних обусловлен наличием соответствующих условий и пропорционален их числу[4]
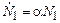 ,
,
число хищников же в отсутствие пищи будет уменьшаться со скоростью
 .
.
При совместном проживании скорости изменения видов будут описываться уже системой уравнений
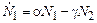 и
и 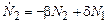 . (2.10)
. (2.10)
Здесь мы предположили, что скорость убывания жертв пропорциональна числу хищников, а скорость размножения последних пропорциональна числу жертв. На самом деле зависимость эта несколько сложнее, и в будущем к ее обсуждению мы еще вернемся. Дифференцируя первое уравнение по времени и исключая скорость изменения хищников, приходим к следующему уравнению для популяции жертв:
 ,
,
которое, по сути, также является уравнением линейного осциллятора, но с дополнительной силой сопротивления, пропорциональной скорости роста популяции и некоторым источниковым членом.
Линейный осциллятор
Итак, мы выяснили, что осциллятор является чрезвычайно популярной моделью. Естественно начать изучение этой модели с простейшего случая линейного осциллятора. Линейный осциллятор – это система, описываемая уравнением (2.3), а если на осциллятор действует внешняя, зависящая от времени сила P (t),
то – уравнением
 (2.11)
(2.11)
Здесь w0 = c / m – постоянная частота собственных (свободных) колебаний линейного осциллятора. Заметим, что в уравне-
нии (2.11) не учитывается возможное наличие силы трения.
Для свободных колебаний (P º 0) решение уравнения (2.11) имеет вид
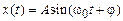 . (2.12)
. (2.12)
Если внешняя сила присутствует и является гармонической, скажем, P = f cos(pt +d), то
 . (2.13)
. (2.13)
В случае резонанса (p = ω0)
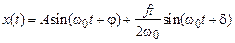 , (2.14)
, (2.14)
т. е. при совпадении частоты вынуждающей гармонической силы с собственной частотой осциллятора  амплитуда вынужденного колебания начинает расти линейно со временем. Здесь следует сделать замечание, что само по себе резонансное усиление колебаний собственной частоты оказывается не столь уж и экзотической ситуацией. Для этого часто не обязательно воздействовать на осциллятор строго резонансным гармоническим возмущением. Дело в том, что довольно широкий класс функций можно разложить в ряд Фурье. если такой функцией подействовать на осциллятор, то это эквивалентно тому, что на него действуют несколько сил с разными частотами (весь ряд Фурье!) и система сама в определенных условиях может «вытаскивать» необходимую ей для усиления частоту. Это происходит, например, в пограничном слое крыла самолета, когда возмущение, появившееся в потоке по той или иной причине (например, из-за шероховатостей поверхности), начинает внезапно резко усиливаться.
амплитуда вынужденного колебания начинает расти линейно со временем. Здесь следует сделать замечание, что само по себе резонансное усиление колебаний собственной частоты оказывается не столь уж и экзотической ситуацией. Для этого часто не обязательно воздействовать на осциллятор строго резонансным гармоническим возмущением. Дело в том, что довольно широкий класс функций можно разложить в ряд Фурье. если такой функцией подействовать на осциллятор, то это эквивалентно тому, что на него действуют несколько сил с разными частотами (весь ряд Фурье!) и система сама в определенных условиях может «вытаскивать» необходимую ей для усиления частоту. Это происходит, например, в пограничном слое крыла самолета, когда возмущение, появившееся в потоке по той или иной причине (например, из-за шероховатостей поверхности), начинает внезапно резко усиливаться.
Решение (2.13) определяет широкий класс колебаний. Разберемся, какие решения являются периодическими. Для периодических решений, не нарушая общности, можно принять d = 0, а за начало отсчета – момент времени, когда скорость  (0) = 0. Если, кроме того, х (0) = A, то решение (2.13) сводится к следующему:
(0) = 0. Если, кроме того, х (0) = A, то решение (2.13) сводится к следующему:
 (2.15)
(2.15)
Это решение будет периодическим в следующих (и только в этих) случаях:
(i) 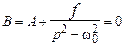 (колебания на собственной час-
(колебания на собственной час-
тоте не возникают);
(ii) 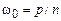 (n – любое целое, B ¹ 0);
(n – любое целое, B ¹ 0);
(iii) 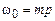 (m – любое целое, кроме единицы, B ¹ 0);
(m – любое целое, кроме единицы, B ¹ 0);
(iv)  (m, n – целые простые числа, B ¹ 0).
(m, n – целые простые числа, B ¹ 0).
В первом случае решение x (t), очевидно, имеет период 2p/ p, равный периоду вынуждающей силы, амплитуда колебаний зависит от частоты свободных колебаний w0. Именно такие колебания будем называть гармоническими (конечно, гармоническими являются и собственные колебания осциллятора). В случае (ii) наименьший период решения (2.15) 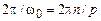 равен периоду свободных колебаний и в n раз больше периода вынужденных. При разложении такого решения в ряд Фурье мы обнаруживаем колебания с частотой, в n раз меньшей частоты вынужденных колебаний. Колебания с пониженными частотами (в сравнении с частотой вынужденных колебаний) называются субгармоническими.
равен периоду свободных колебаний и в n раз больше периода вынужденных. При разложении такого решения в ряд Фурье мы обнаруживаем колебания с частотой, в n раз меньшей частоты вынужденных колебаний. Колебания с пониженными частотами (в сравнении с частотой вынужденных колебаний) называются субгармоническими.
В случае (iii) решение имеет период, равный периоду внешней силы 2p/ p, как и в случае (i). Однако эти колебания разные. Случай (iii) представляет собой наложение двух колебаний, наименьшие периоды которых различны, тогда как гармонические колебания (случай (i)) состоят из одной гармоники. Колебания в случае (iii) называют ультрагармоническими.
Наконец, для случая (iv) решение x (t) имеет период 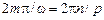 , тогда как внешняя сила имеет период
, тогда как внешняя сила имеет период  . Следовательно, наименьший период колебаний здесь такой же, как и в случае (ii) (в n раз больше периода внешних колебаний). Вместе с тем, период этих колебаний не совпадает с периодом свободных колебаний, а в m раз больше послед-него.
. Следовательно, наименьший период колебаний здесь такой же, как и в случае (ii) (в n раз больше периода внешних колебаний). Вместе с тем, период этих колебаний не совпадает с периодом свободных колебаний, а в m раз больше послед-него.
На реальные осцилляторы действуют силы сопротивления, в результате собственные колебания всегда оказываются затухающими (а в некоторых случаях могут не возникнуть вовсе). При наличии силы трения колебания (ii), (iii) и (iv), для существования которых требуется одновременное наличие собственных и вынужденных колебаний, никогда не будут наблюдаться, так как свободные колебания затухают. То есть в линейной системе тогда будут иметь место только гармонические колебания с частотой вынуждающей силы. Замечательным, однако, является то обстоятельство, что в нелинейных системах все четыре случая могут иметь место и при наличии вязкого трения.
Точка всегда обозримей в конце прямой.
Иосиф Бродский
Нелинейные колебания
3.1. Свободные колебания осциллятора
с квадратичной нелинейностью. Метод малого параметра
Для рассмотрения свойств осциллятора с квадратичной нелинейностью учтем в правой части уравнения (2.4) только два первых члена и запишем его в стандартной форме
 . (3.1)
. (3.1)
Будем далее предполагать, что нелинейный член мал, т. е.
e << 1. Уравнение (3.1) легко интегрируется, если воспользоваться равенством 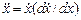 . Однако в общем случае, например, в задачах с трением, когда в уравнение входит и член, пропорциональный
. Однако в общем случае, например, в задачах с трением, когда в уравнение входит и член, пропорциональный  , проинтегрировать соответствующее уравнение аналитически не удается. Поэтому ниже мы будем пользоваться приближенным методом – методом малого параметра, пригодным для произвольных нелинейных уравнений. Единственным условием его применения является наличие малого параметра.
, проинтегрировать соответствующее уравнение аналитически не удается. Поэтому ниже мы будем пользоваться приближенным методом – методом малого параметра, пригодным для произвольных нелинейных уравнений. Единственным условием его применения является наличие малого параметра.
Так как e << 1, решение уравнения (3.1) можно искать в виде ряда
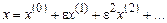 (3.2)
(3.2)
Подставляя (3.2) в уравнение (3.1), получаем уравнение


Собирая члены с одинаковыми степенями малого параметра e и приравнивая их суммы к нулю, получим бесконечную систему уравнений
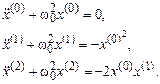 (3.3)
(3.3)
.......................................
Первое уравнение – хорошо известное линейное уравнение свободного гармонического осциллятора с частотой w0. Иногда его называют порождающим. Соответствующее решение имеет вид (2.12). Поскольку мы интересуемся периодическими решениями, найдется время t 0, когда х будет достигать максимального значения, а поэтому 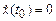 . Не нарушая общности, можно принять
. Не нарушая общности, можно принять  . Будем строить решение поэтому при следующих начальных данных:
. Будем строить решение поэтому при следующих начальных данных:

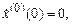
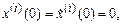
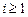 . (3.3а)
. (3.3а)
Тогда
 , (3.4)
, (3.4)
а второе уравнение системы (3.3) принимает вид
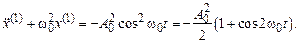 (3.5)
(3.5)
Его решение
 (3.6)
(3.6)
Здесь постоянные В 1 и j1 определяются из нулевых начальных условий (3.3а). Решение (3.6) отличается тем, что за счет нелинейности появляются колебания с удвоенной собственной час-тотой.
Если бы мы продолжили процесс последовательных приближений, то обнаружили также колебания с частотами w n = n w0, где n ³ 2 (n – целое число). Эти частоты называются комбинационными. Поскольку все w n > w0, их называют еще супергармониками. Чем выше номер приближения (см. ряд (3.2)), тем более высокие частоты обнаруживаются в колебательной системе. К сожалению, наряду с комбинационными частотами (½ n ½ ¹ 1) уже во втором приближении в правой части появляется резонансная частота. Действительно, правая часть третьего уравнения систе-
мы (3.3)
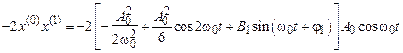
содержит резонансный член 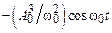 и другие, появляющиеся из произведений cos2w0 t ×cosw0 t и sin(w0 t + j1)cosw0 t.
и другие, появляющиеся из произведений cos2w0 t ×cosw0 t и sin(w0 t + j1)cosw0 t.
Таким образом, несмотря на то что мы рассматриваем движение свободного осциллятора (см. уравнение (3.1)), на который не действуют никакие внешние силы, получающееся решение содержит резонансные члены, как если бы на систему действовала вынуждающая внешняя гармоническая сила. В результате в решении появляются растущие со временем члены, которые называют секулярными. Подобное поведение решения свидетельствует о систематическом дефекте используемого метода решения уравнения (3.1). Метод решения уравнения (3.1) в виде ряда (3.2) по малому параметру позволяет получить разумные нулевое и первое приближения, однако в высших приближениях этот метод применять нельзя. Необходима его корректировка. Метод решения уравнения нелинейного осциллятора в виде ряда по малому параметру, равномерно пригодный также и в высших приближениях, был развит усилиями многих исследователей и в первую очередь А. Пуанкаре. обсудим идею этого метода и его приме-нение.



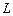 и конденсатора
и конденсатора  соединенных между собой проводниками. Если разность потенциалов на пластинах конденсатора в момент времени
соединенных между собой проводниками. Если разность потенциалов на пластинах конденсатора в момент времени 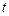 равна
равна 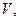 то заряд конденсатора
то заряд конденсатора  Если емкость конденсатора постоянна, то уравнение движения заряда в цепи – это уравнение линейного осциллятора
Если емкость конденсатора постоянна, то уравнение движения заряда в цепи – это уравнение линейного осциллятора . (2.9)
. (2.9)
 и их жертв
и их жертв  . В отсутствие хищников рост последних обусловлен наличием соответствующих условий и пропорционален их числу[4]
. В отсутствие хищников рост последних обусловлен наличием соответствующих условий и пропорционален их числу[4]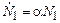 ,
, .
.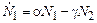 и
и 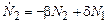 . (2.10)
. (2.10) ,
, (2.11)
(2.11)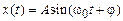 . (2.12)
. (2.12) . (2.13)
. (2.13)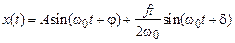 , (2.14)
, (2.14) амплитуда вынужденного колебания начинает расти линейно со временем. Здесь следует сделать замечание, что само по себе резонансное усиление колебаний собственной частоты оказывается не столь уж и экзотической ситуацией. Для этого часто не обязательно воздействовать на осциллятор строго резонансным гармоническим возмущением. Дело в том, что довольно широкий класс функций можно разложить в ряд Фурье. если такой функцией подействовать на осциллятор, то это эквивалентно тому, что на него действуют несколько сил с разными частотами (весь ряд Фурье!) и система сама в определенных условиях может «вытаскивать» необходимую ей для усиления частоту. Это происходит, например, в пограничном слое крыла самолета, когда возмущение, появившееся в потоке по той или иной причине (например, из-за шероховатостей поверхности), начинает внезапно резко усиливаться.
амплитуда вынужденного колебания начинает расти линейно со временем. Здесь следует сделать замечание, что само по себе резонансное усиление колебаний собственной частоты оказывается не столь уж и экзотической ситуацией. Для этого часто не обязательно воздействовать на осциллятор строго резонансным гармоническим возмущением. Дело в том, что довольно широкий класс функций можно разложить в ряд Фурье. если такой функцией подействовать на осциллятор, то это эквивалентно тому, что на него действуют несколько сил с разными частотами (весь ряд Фурье!) и система сама в определенных условиях может «вытаскивать» необходимую ей для усиления частоту. Это происходит, например, в пограничном слое крыла самолета, когда возмущение, появившееся в потоке по той или иной причине (например, из-за шероховатостей поверхности), начинает внезапно резко усиливаться.  (0) = 0. Если, кроме того, х (0) = A, то решение (2.13) сводится к следующему:
(0) = 0. Если, кроме того, х (0) = A, то решение (2.13) сводится к следующему: (2.15)
(2.15)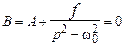 (колебания на собственной час-
(колебания на собственной час-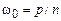 (n – любое целое, B ¹ 0);
(n – любое целое, B ¹ 0);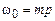 (m – любое целое, кроме единицы, B ¹ 0);
(m – любое целое, кроме единицы, B ¹ 0); (m, n – целые простые числа, B ¹ 0).
(m, n – целые простые числа, B ¹ 0).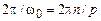 равен периоду свободных колебаний и в n раз больше периода вынужденных. При разложении такого решения в ряд Фурье мы обнаруживаем колебания с частотой, в n раз меньшей частоты вынужденных колебаний. Колебания с пониженными частотами (в сравнении с частотой вынужденных колебаний) называются субгармоническими.
равен периоду свободных колебаний и в n раз больше периода вынужденных. При разложении такого решения в ряд Фурье мы обнаруживаем колебания с частотой, в n раз меньшей частоты вынужденных колебаний. Колебания с пониженными частотами (в сравнении с частотой вынужденных колебаний) называются субгармоническими.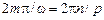 , тогда как внешняя сила имеет период
, тогда как внешняя сила имеет период  . Следовательно, наименьший период колебаний здесь такой же, как и в случае (ii) (в n раз больше периода внешних колебаний). Вместе с тем, период этих колебаний не совпадает с периодом свободных колебаний, а в m раз больше послед-него.
. Следовательно, наименьший период колебаний здесь такой же, как и в случае (ii) (в n раз больше периода внешних колебаний). Вместе с тем, период этих колебаний не совпадает с периодом свободных колебаний, а в m раз больше послед-него. . (3.1)
. (3.1)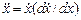 . Однако в общем случае, например, в задачах с трением, когда в уравнение входит и член, пропорциональный
. Однако в общем случае, например, в задачах с трением, когда в уравнение входит и член, пропорциональный 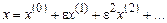 (3.2)
(3.2)

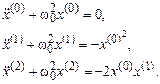 (3.3)
(3.3)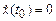 . Не нарушая общности, можно принять
. Не нарушая общности, можно принять  . Будем строить решение поэтому при следующих начальных данных:
. Будем строить решение поэтому при следующих начальных данных:
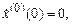
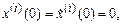
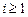 . (3.3а)
. (3.3а) , (3.4)
, (3.4)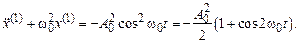 (3.5)
(3.5) (3.6)
(3.6)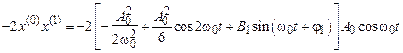
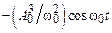 и другие, появляющиеся из произведений cos2w0 t ×cosw0 t и sin(w0 t + j1)cosw0 t.
и другие, появляющиеся из произведений cos2w0 t ×cosw0 t и sin(w0 t + j1)cosw0 t.


