Difficillimum autem est, in omni
conquisitione rationis exordium[2].
Платон
Материальная точка. Движение в центральном
Потенциальном поле
Модель материальной точки является одной из важнейших, поскольку в той или иной мере служит исходным материалом для построения большинства существующих моделей. Связано это с тем, что материальной точкой мы можем моделировать любой объект, если его размерами и внутренней структурой в данной задаче можно пренебречь. Чтобы задать положение материальной точки, нужно ввести систему координат. Ее начало связывают с некоторым телом, которое называют телом отсчета и именно относительно этого тела определяют положение материальной точки. Пространство, в котором движутся изучаемые нами системы, обычно считают евклидовым. Сегодня мы знаем, что это идеализация, которая, однако, неплохо описывает в большинстве возникающих задач реальное пространство. Задать евклидово пространство можно, введя некоторую ортогональную систему отсчета, например прямоугольную декартову систему координат  с началом в точке О. Положение материальной точки
с началом в точке О. Положение материальной точки 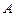 тогда в данный момент времени
тогда в данный момент времени 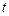 задается радиусом-вектором
задается радиусом-вектором  (рис. 1.1). Изолированная материальная точка движется так, что ее скорость
(рис. 1.1). Изолированная материальная точка движется так, что ее скорость  не меняется со временем.
не меняется со временем.
|
| |  |
Рис.1.1. Траектория материальной точки
относительно системы координат Oxyz
В случае, если данная материальная точка взаимодействует с другими объектами или полями, на нее будет действовать система сил 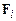 . Движение материальной точки управляется тогда дифференциальным уравнением Ньютона
. Движение материальной точки управляется тогда дифференциальным уравнением Ньютона
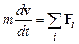 , (1.1)
, (1.1)
где 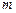 – масса точки.
– масса точки.
Сила может быть функцией и времени, и координат, и скоростей точки, поэтому в общем случае мы имеем нелинейное дифференциальное уравнение второго порядка
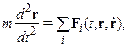 (1.1а)
(1.1а)
исчерпывающее решение которого построить удается нечасто.
Рассмотрим так называемую задачу двух тел на примере движения планеты  (тело 1) в гравитационном поле звезды
(тело 1) в гравитационном поле звезды 
(тело 2). Движение этих двух тел относительно некоторой инерциальной системы координат описывается системой уравнений
 ,
,  , (1.2)
, (1.2)
где силы взаимодействия  определяются законом всемирного тяготения, так что уравнения движения (1.2) принимают вид
определяются законом всемирного тяготения, так что уравнения движения (1.2) принимают вид
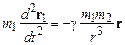 ,
, 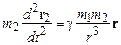 , (1.2а)
, (1.2а)
где мы ввели относительную координату  (рис. 1.2),
(рис. 1.2), 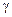 – гравитационная постоянная.
– гравитационная постоянная.
Рис. 1.2. Ориентация подвижной системы координат Sxyz,
связанной с материальной точкой S, относительно исходной
неподвижной OXYZ
Систему уравнений (1.2а) особенно легко проинтегрировать в подвижной системе координат, центр которой связан с материальной точкой  (звездой) (см. рис. 1.2). Уравнения движения (1.2а) в этом случае сводятся к уравнению, определяющему движение планеты относительно звезды
(звездой) (см. рис. 1.2). Уравнения движения (1.2а) в этом случае сводятся к уравнению, определяющему движение планеты относительно звезды
 , (1.3)
, (1.3)
что эквивалентно движению точки  в поле центральной силы
в поле центральной силы  .
.
Уравнение (1.3) уже достаточно легко интегрируется. Мы не будем приводить явного решения задачи, но обратим внимание на два важных момента. Первый состоит в том, что исходную задачу двух тел удалось свести к задаче о движении одной материальной точки в некотором поле. Почему это удалось сделать? Общее решение задачи двух тел должно содержать шесть независимых первых интегралов и шесть независимых вторых интегралов. Для замкнутой системы двух взаимодействующих материальных точек существует несколько интегралов движения, связанных с выполнением в такой системе законов сохранения полной механической энергии (суммы кинетической и потенциальной энергий системы)
 , (1.4)
, (1.4)
полного импульса
 (1.5)
(1.5)
и полного момента импульса системы
 . (1.6)
. (1.6)
Выполнение этих законов сохранения и позволяет упростить задачу и делает систему уравнений (1.2) интегрируемой[3].
Второе обстоятельство связано с численным решением уравнений (1.2). Такое решение легко построить, вводя вместо производных соответствующие конечные разности. При этом можно использовать численные схемы разного порядка точности. Какой из них даст решение, лучше всего аппроксимирующее точное? В качестве критерия здесь следует снова использовать законы сохранения. То, насколько хорошо они будут выполняться при решении, и скажет вам, точно или нет она решается.
Задача двух тел родилась в небесной механике, и при ее решении были неплохо вычислены орбиты планет Солнечной системы. Однако естественным продолжением явилась задача трех тел: планета – планета – звезда, описываемая системой уравнений
 ,
, 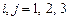 . (1.7)
. (1.7)
Здесь, как и обычно, заданы начальные положения и скорости всех трех тел (материальных точек). Для этой системы, так же как и для двух тел, выполняются законы сохранения импульса, момента импульса и энергии. Эта задача скрупулезно исследовалась А. Пуанкаре, который и показал, что она не интегрируема, не хватает законов сохранения. Установлено, что не существует кроме указанных законов сохранения других интегралов движения, которые однозначно выражались бы через алгебраические или однозначные трансцендентные функции координат и скоростей рассматриваемых материальных точек. Парадоксальность ситуации состоит еще и в том, что решить численно систему трех уравнений
 ,
, 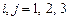 ,
,
описывающую гравитационное взаимодействие трех тел, казалось бы, совсем несложно. Думаю, это смог бы сделать любой из читающих эту книгу. Выяснилось, однако, что получающиеся решения ведут себя довольно «капризно», они оказываются неустойчивыми по отношению к малым изменениям начальных данных и других параметров задачи. Более того, если в задаче двух тел в зависимости от начальных данных тела двигаются по достаточно простым траекториям (параболе, гиперболе или эллипсу), то здесь могут появляться чрезвычайно сложные хаотические траектории.
Значительно бóльшие успехи были получены при решении так называемой ограниченной задачи трех тел, когда третье тело рассматривается в качестве малого возмущения. Эта задача может быть решена методом возмущений. Именно так при решении задачи о движении планеты Уран было предсказано существование еще одной планеты Солнечной системы – Нептуна. Однако и здесь задача не интегрируется в квадратурах.
Красота обладает общими правилами,
приложимыми к различным вещам: не
только к формам, но также к действиям
и идеям.
Готхольд Эфраим Лессинг



 с началом в точке О. Положение материальной точки
с началом в точке О. Положение материальной точки 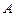 тогда в данный момент времени
тогда в данный момент времени 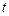 задается радиусом-вектором
задается радиусом-вектором  (рис. 1.1). Изолированная материальная точка движется так, что ее скорость
(рис. 1.1). Изолированная материальная точка движется так, что ее скорость  не меняется со временем.
не меняется со временем.
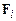 . Движение материальной точки управляется тогда дифференциальным уравнением Ньютона
. Движение материальной точки управляется тогда дифференциальным уравнением Ньютона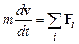 , (1.1)
, (1.1)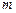 – масса точки.
– масса точки.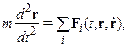 (1.1а)
(1.1а) (тело 1) в гравитационном поле звезды
(тело 1) в гравитационном поле звезды 
 ,
,  , (1.2)
, (1.2) определяются законом всемирного тяготения, так что уравнения движения (1.2) принимают вид
определяются законом всемирного тяготения, так что уравнения движения (1.2) принимают вид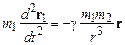 ,
, 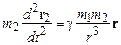 , (1.2а)
, (1.2а) (рис. 1.2),
(рис. 1.2), 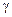 – гравитационная постоянная.
– гравитационная постоянная.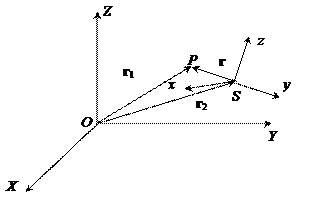
 , (1.3)
, (1.3) .
. , (1.4)
, (1.4) (1.5)
(1.5) . (1.6)
. (1.6) ,
,  . (1.7)
. (1.7) ,
, 


