Задачи, связанные с построением истинной величины углов

Решая типовые задачи, мы научились строить истинную величину углов между геометрическими элементами. Однако можно столкнуться с необходимостью построить элемент, который бы составлял заданный угол с другим, уже имеющимся элементом. Такие задания, как правило, проверяют знание положения о том, что угол проецируется в натуральную величину на некоторую плоскость проекций, если обе его стороны параллельны этой плоскости, т. е. угол лежит в плоскости уровня.

На рисунке 75 рассматривается решение задачи, в которой через точку С необходимо

построить прямую, составляющую с заданной прямой АВ угол 60.

 

I

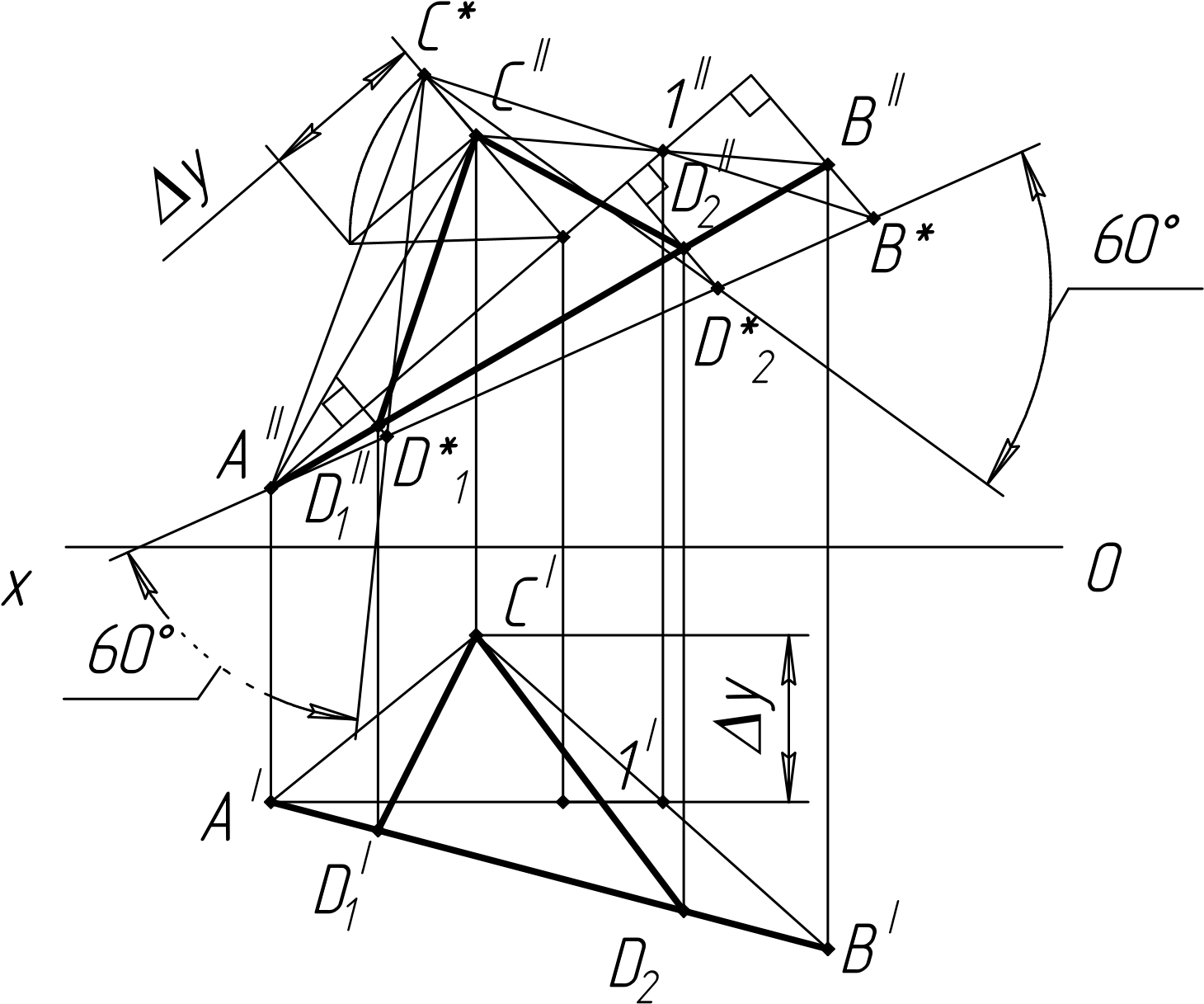
Рисунок 75 – Задача, связанная с построением угла между пересекающимися прямыми

Точка С и прямая АВ определяют плоскость, содержащую заданный угол. Ее необходимо преобразовать в плоскость уровня, чтобы построить истинную величину угла. Это можно выполнить двумя переменами плоскостей проекций. Однако метод вращения позволяет сделать это с меньшим объемом построений.

Объединим точку С и отрезок АВ в треугольник. Проведем в его пределах фронталь А1:

горизонтальная проекция A’1’ параллельна оси Оx, фронтальная A’’1’’ строится в проекционной связи. Отрезок A’’1’’ проецируется в натуральную величину – его можно использовать в качестве оси вращения. Строим истинную величину треугольника ABC вращением относительно фронтали. Положение точки C* определяем за счет построения истинной величины радиуса ее вращения. Точку B* находим, проведя отрезок прямой С*1’’ до пересечения с траекторией движения точки B’’. Соединяем точки A’’, В* и С* – полученный треугольник отображается в истинную величину. Вся плоскость, заданная точкой С и отрезком АВ, стала параллельной фронтальной плоскости проекций, поэтому мы можем в ней построить любой угол в истинную величину.

Проводим два отрезка C*D*₁ и C*D*₂, составляющие заданный угол (60) с прямой A’’B*. Теперь их следует возвратить в исходные проекции. Фронтальные проекции точек D’’₁ и D’’₂ находим на пересечении траекторий их вращения, перпендикулярных A’’1’’, с отрезком A’’B’’. Точки D’₁ и D’₂ на горизонтальной плоскости проекций определяем, пользуясь проекционными связями. Соединяем полученные проекции точек D₁ и D₂ с соответствующей проекцией точки С – задача решена.

Если требуется построить прямой I I угол, можно также действовать C

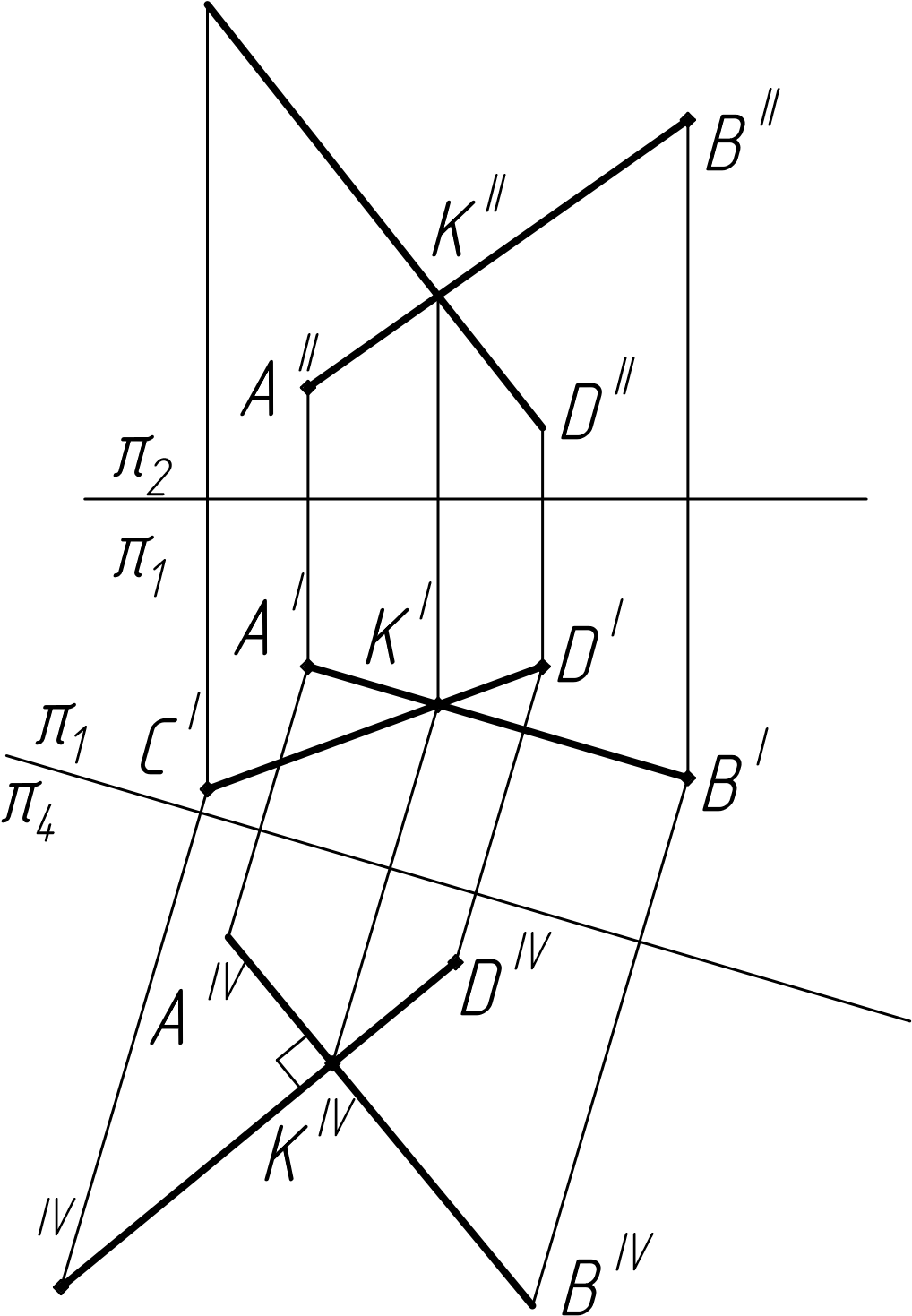
аналогичным образом. Однако следует вспомнить, что угол в 90 отображается в натуральную величину, если всего одна из его сторон параллельна некоторой плоскости проекций. Задача, связанная с построением прямого угла, рассмотрена на рисунке 76.

Пусть заданы две проекции прямой АВ и горизонтальная проекция прямой CD. Требуется построить C’’D’’, если известно, что прямая CD пересекает АВ под углом 90.

Воспользуемся методом перемены плоскостей проекций. Проведем новую ось абсцисс π₁/π₄ параллельно A’B’. Построим измененную фронтальную проекцию отрезка АВ – A^IVB^IV. Эта проекция является истинной длиной отрезка, поэтому прямой угол, составленный с прямой АВ, в этой плоскости проекций будет отображаться без искажений.

Известно, что прямые пересекаются. Поэтому точка пересечения горизонтальных проекций является проекцией пересечения самих прямых АВ и CD. Обозначим ее К. С помощью проекционной связи найдем K^IV и проведем через нее прямую, перпендикулярную A^IVB^IV. Также используя проекционные связи, отметим на ней точки C^IV и D^IV.

Остается перенести прямую CD в C исходную фронтальную плоскость проекций. Мы можем воспользоваться проекционной

связью и обозначить точку K’’. После этого мы Рисунок 76 – Задача на построение прямого угла можем построить одну из крайних точек отрезка между пересекающимися прямыми

C’’D’’, используя ее координату z, измеренную в плоскости проекций π₄. Пусть таким образом будет построена точка C’’. Тогда, после того как проведена прямая C’’K’’, точку D’’ находим на ней в проекционной связи с D’.

24 Контрольные вопросы по разделу «Начертательная геометрия»

1. Точка общего и частного положения на эпюре и в косоугольной фронтальной диметрической проекции.

2. Точка общего и частного положения на эпюре и в прямоугольной изометрической проекции.

3. Прямая общего и частного положения. Способы определения истинной величины отрезка прямой.

4. Прямая общего положения: определение следов прямой и разбиение отрезка прямой по частям пространства.

5. Прямая частного положения: определение следов прямой и разбиение отрезка прямой по частям пространства.

6. Способы задания плоскости. Определение следов плоскости, заданной другими геометрическими элементами.

7. Плоскости общего и частного положения. Особые свойства плоскостей частного положения, примеры их использования.

8. Принадлежность прямой общего и частного положения плоскости: построение проекций фигуры, лежащей в плоскости.

9. Принадлежность точки плоскости. Построение проекций элементов, принадлежащих плоскости, заданной плоской фигурой.

10. Параллельные прямые и плоскости. Построение недостающей проекции прямой, параллельной заданной плоскости. Построение плоскости, проходящей через заданную точку и параллельной заданной плоскости.

11. Проецирование углов между пересекающимися прямыми. Прямая, перпендикулярная плоскости. Построение плоскости, проходящей через заданную точку и перпендикулярной заданной прямой.

12. Взаимно перпендикулярные плоскости. Построение плоскости, проходящей через заданную прямую и перпендикулярной заданной плоскости.

13. Определение линии пересечения плоскостей, заданных следами.

14. Определение линии пересечения плоскостей, по крайней мере, одна из которых не задана следами.

15. Определение точки встречи (пересечения) прямой и плоскости.

16. Конкурирующие точки, их использование для определения видимости отрезков прямой при пересечении с плоскостью.

17. Перевод прямых и плоскостей общего положения в частное положение методом перемены плоскостей проекций.

18. Определение истинной величины плоской фигуры методом перемены плоскостей проекций.

19. Построение отрезка кратчайшего расстояния между точкой и прямой, между точкой и плоскостью методом перемены плоскостей проекций.

20. Построение отрезка кратчайшего расстояния между параллельными прямыми, между прямой и параллельной ей плоскостью методом перемены плоскостей проекций.

21. Построение отрезка кратчайшего расстояния между скрещивающимися прямыми, между параллельными плоскостями методом перемены плоскостей проекций.

22. Определение угла наклона прямых и плоскостей к плоскостям проекций методом перемены плоскостей проекций.

23. Вращение точки относительно оси, перпендикулярной плоскости проекций. Определение истинной длины отрезка прямой и угла наклона прямой к плоскости проекций методом вращения.

24. Вращение плоскости относительно фронтали или горизонтали: определение истинной величины плоской фигуры методом вращения.

25. Вращение плоскости относительно фронтали или горизонтали: определение истинной величины угла между пересекающимися прямыми.

26. Вращение плоскости относительно фронтали или горизонтали: определение истинной величины угла между прямой и плоскостью.

27. Вращение плоскости относительно фронтали или горизонтали: определение истинной величины угла между плоскостями.

28. Определение поверхности. Многогранники. Определение проекций фигуры сечения многогранника проецирующей плоскостью.

29. Линейчатые поверхности с одной независимой направляющей. Конические поверхности. Определение проекций фигуры сечения конуса проецирующей плоскостью.

30. Линейчатые поверхности с одной независимой направляющей. Цилиндрические поверхности. Определение проекций фигуры сечения цилиндра проецирующей плоскостью.

Перечисленные темы будут использованы в качестве 1-го вопроса в экзаменационных билетах по курсу «Начертательная геометрия». При ответе на данный вопрос следует привести не менее 3 графических примеров, иллюстрирующих теоретические положения или демонстрирующих прикладное значение темы.

Список литературы

1. Гордон, В.О. Курс начертательной геометрии: учебное пособие для втузов / В.О. Гордон, М.А. Семенцов-Огиевский; под ред. В.О. Гордона (24-е изд. – ред. Ю.Б. Иванов). – 27-е изд., стер. – М.: Высшая школа, 2006. – 272 с.

2. Гордон, В.О. Сборник задач по курсу начертательной геометрии: учебное пособие для втузов / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева; под ред. Ю.Б. Иванова. – 12-е изд., стер. – М.: Высшая школа, 2006. – 320 с.

3. Фролов, С.А. Начертательная геометрия: учебное пособие / С.А. Фролов – М.: Инфра, 2007. – 285 с.

 

 

Кафедра инженерного проектирования

Учебное пособие

Начертательная геометрия

Игорь Иванович Гнилуша

Владимир Александрович Люторович

Виктор Трифонович Кривой

Ростислав Борисович Соколов

I FlvPZOBMARbF5UWOmfUjb2jYxkpJCYcMDdQxdpnWoazJYZj5jli8g+8dRjn7StseRyl3rb5Nkgft sGFZqLGjVU3lcXtyBt5GHJfz9GVYHw+r89fu/v1znZIx11fT8hlUpCn+heEHX9ChEKa9P7ENqjUg j8RfFe/pLp2D2ksoAV3k+j978Q0AAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAA AAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAA AJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQC+CCahgwIA AF0GAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQB1VnyM 2gAAAAMBAAAPAAAAAAAAAAAAAAAAAN0EAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAA 5AUAAAAA ">

Отпечатано с оригинал-макета. Формат __ Печ.л. __. Тираж ___ экз.

 

U iMgWW89k4EwBFsXlRY6Z9SNvaNjGSkkJhwwN1DF2mdahrMlhmPmOWLyD7x1GOftK2x5HKXetvk2S B+2wYVmosaNVTeVxe3IG3kYcl/P0ZVgfD6vz1+7+/XOdkjHXV9PyGVSkKf6F4Qdf0KEQpr0/sQ2q NSCPxF8V7+kunYPaSygBXeT6P3vxDQAA//8DAFBLAQItABQABgAIAAAAIQC2gziS/gAAAOEBAAAT AAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhADj9If/W AAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhAGSyl2OF AgAAXQYAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0AFAAGAAgAAAAhAHVW fIzaAAAAAwEAAA8AAAAAAAAAAAAAAAAA3wQAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPMA AADmBQAAAAA= ">

Санкт-Петербургский государственный технологический институт

(Технический университет)

 

I FlvPZOBMARbF5UWOmfUjb2jYxkpJCYcMDdQxdpnWoazJYZj5jli8g+8dRjn7StseRyl3rb5Nkgft sGFZqLGjVU3lcXtyBt5GHJfz9GVYHw+r89fu/v1znZIx11fT8hlUpCn+heEHX9ChEKa9P7ENqjUg j8RfFe/pLp2D2ksoAV3k+j978Q0AAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAA AAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAA AJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQDt2deUgwIA AF0GAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQB1VnyM 2gAAAAMBAAAPAAAAAAAAAAAAAAAAAN0EAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAA 5AUAAAAA ">

190013, Санкт-Петербург, Московский пр., 26

 

 

[1] Результат алгебраической разности может быть получен построением, если отложить на построенном перпендикуляре расстояние, равное «недостающей координате» одной из крайних точек отрезка, а потом из полученной точки отложить вторую «недостающую координату»: в том же направлении - при различных знаках координат концов отрезка или в противоположном при их совпадении.