| Вид рыбы
| Действительный состав уловов по анализам
| Длина
|
| Кг
| %
| См
|
| Плотва
Окунь
Ёрш
|
| 9,3
8,6
17,1
| 4(9-11)15
4(7-12)18
3(5-7)11
|
Второй способ обработки материалов применяется для наиболее ценных и охраняемых видов рыб. При этом первый и второй пункты такие же как в первом способе, то есть анализы, относящиеся к тому или иному типу орудий лова, объединяются в одну группу, затем в каждом анализе число рыб, относящееся к определенному классовому промежутку, умножается на коэффициент пересчета. Полученные размерные ряды каждого вида выписывают из всех анализов и суммируют в сводный ряд, одновременно суммируя и массу рыбы в этих рядах. Далее пользуются вспомогательными таблицами действительного видового состава уловов, а с помощью переводного коэффициента получают численность вида в весовом и абсолютном выражении (табл. 17).
Таблица 17
Численность вида в штучно-весовом выражении
| Товарные сорта принятой рыбы
| Масса рыбы в товарных сортах, ц
| Действительная масса принятого леща, ц
| Проанализировано только леща
| Переводной коэффициент
| Численность выловленного леща по сортам, тыс. экз.
|
| масса, ц
| кол-во, тыс. шт.
|
| Лещ кр. и ср.
|
|
| 13,5
| 1,2
| 47,0
| 56,4
|
| Щука кр.
|
|
| 5,2
| 0,6
| 12,9
| 7,2
|
| Разная мелочь
|
|
| 38,6
| 1,2
| 15,2
| 18,2
|
Например, масса леща в сорте «лещ крупный и средний» во всем улове составляет 635 ц, при этом масса измеренного леща (1,2 тыс. экз.) во всех анализах того же сорта составляет 13,5 ц, то есть переводной коэффициент будет 635:13,5=47,0, а число рыб в данном сорте – 1,2 тыс.´47,0=56,4 тыс. На полученный коэффициент умножают соответственно все цифры в классах размерно-возрастного ряда леща в данном сорте.
Суммарный числовой ряд в отдельных классах длины разбивают на возрастные группы. В результате весь улов изучаемого вида из каждого орудия лова будет выражен не только в весовом, но и в количественном выражении по отдельным возрастным группам в абсолютных значениях и в процентах.
Вывод: анализ размерно-весового состава дает возрастной состав промысловых уловов в процентах, а объединенные в таблицу количественно-возрастные характеристики данного вида по всем орудиям лова – сравнительную характеристику промыслового воздействия рыболовства на запасы данного вида.
Контрольные вопросы и задания
1. Массовая проба.
2. Выборочная проба.
3. Средняя проба.
4. Размерно-возрастной ключ.
5. Переводной коэффициент.
6. Метод осреднения.
II. Вариационно-статистическая обработка
биологического материала
Современная биология развивается исключительно быстрыми темпами. Одним из важных факторов, стимулирующих дальнейшее развитие различных областей естественных наук, является внедрение в них математики.
Широкое использование математики в ихтиологии началось в пятидесятых годах прошлого столетия, до этого она развивалась на основе качественного анализа явлений
Основы биометрии как науки о применении математических методов для изучения живых существ, были разработаны Гальтоном (1899).
Для внедрения математики в биологию имелись очень серьезные причины. Одной из них был переход от описательного метода изучения явлений к экспериментальному, а эксперимент неизбежно требовал количественной оценки явлений процессов.
При постановке экспериментов потребовалась разработка схем опытов, методы математического анализа результатов опыта и способы доказательства достоверности того или иного фактора.
Наконец, важнейшим обстоятельством, определившим применение математических и в частности математико-статистических методов, явилось установление факта, что многим биологическим явлениям свойственны статистические закономерности, обнаруживаемые при изучении совокупности, но не приложимые к отдельным единицам совокупности. При изучении биологических совокупностей, являющихся типично статистическими, оказалось целесообразно применять методы математической статистики, которую в применении к биологии стали называть биологической статистикой.
Группировка данных, совокупность и вариационный ряд
Всякое множество отдельных, отличающихся друг от друга и вместе с тем сходных в некоторых существенных отношениях объектов составляет так называемую совокупность. Совокупностями являются, например, особи какого-либо вида рыб из улова. В состав совокупности входят различные члены или единицы, т.е. каждая отдельная рыба. Обычно число единиц совокупности называют объемом совокупности и обозначают латинской буквой n. Единица совокупности может характеризоваться определенными признаками, например, длина и масса рыбы в какой-то пробе. Каждый изучаемый признак принимает разные значения у различных единиц совокупности, он меняется в своем значении от одной единицы совокупности к другой. Это различие между единицами совокупности называется вариацией или дисперсией (т.е. рассеиванием). Мы говорим «признак варьирует». Это означает, что он принимает разные значения у разных признаков у разных членов совокупности. Значение или меру признака называют вариантой и обозначают латинской буквой х. В таком случае ряд вариант в совокупности следует обозначить как х 1 х 2 х 3 … хп. Общее обозначение любой варианты хi. Значок i – порядковый номер варианты.
Совокупность может состоять из других более частных совокупностей, так, например, общая проба из улова, разделенная по сортам или видам рыб. Наиболее общую совокупность называют генеральной. Генеральная совокупность может состоять из большего количества единиц, изучить которые все не представляется возможным. Поэтому практически приходится иметь дело со сравнительно небольшими, выборочными совокупностями.
При изучении единиц совокупности по тем или другим признакам необходимо записать полученные данные. Лучше всего эти записи производить на карточках, которые можно группировать любым способом, или в ихтиологическом журнале. При большом объеме собранных материалов обработка может производиться счетной техникой.
Способ обработки данных зависит от характера вариации изучаемых признаков. Различия между вариантами могут быть прерывными (дискретными) и непрерывными. В первом случае они выражаются целыми числами, между которыми нет и не может быть перехода. Например, количество лучей в плавниках.
При непрерывной вариации значения вариант необязательно выражаются только целыми числами. Все зависит от степени точности, которая принимается для характеристики данного количественного признака, например, граммы для обозначения массы рыб, миллиграммы – для обозначения массы кормовых организмов.
Однако во всех этих и подобных случаях существует непрерывная вариация, выражающаяся в том, что между вариантами возможны все переходы
Группировка данных при количественной дискретной вариации
При количественной вариации необходимо предварительно наметить классы, охватывающие все полученные количественные данные, от минимальных от максимальных. Группировку отдельных вариант лучше всего провести по значениям отдельных вариант. Например, число лучей в горизонтальном ряду варьирует от 45 до 54. Составляется таблица с намеченными 9-ю классами и в соответствующие горизонтальные строчки разносятся все варианты, начиная от первой. Обозначаются они так: первые четыре варианты данного класса точками, а последующие – черточками, соединяющими четыре точки. Число 10 в таком случае будет фигурой 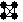 .
.
В случае если дискретный признак сильно варьирует, лучше наметить классы, охватывающие несколько значений вариант, например, 40-41 или 40-42.
Вопрос о распределении выборки в безынтервальный и интервальный ряды решается в зависимости от размаха и характера варьирования признака. Если признак варьирует дискретно и слабо, то есть в узких границах, выборка распределяется в безынтервальный ряд, если же в широком диапазоне, то независимо от того, как варьирует признак, дискретно или непрерывно, выборка распределяется в интервальный ряд. При этом важно, чтобы намечаемая ширина классового интервала удовлетворяла определенным требованиям.
Дело в том, что построение вариационного ряда преследует двоякую цель: выявление закономерности варьирования признака и как способ, облегчающий вычисление статистических характеристик варьирующего объекта.
Грубая группировка исходных данных, когда намечаются слишком широкие или слишком узкие классовые интервалы, скажется на точности определения числовых характеристик. Приблизительно оптимальное число классов К определяют по следующей таблице 18.
Таблица 18
Объем выборки и число классов при вычислении
статистических характеристик
| Объем выборки (от (от-до)
| Число классов
|
| 25-40
| 5-6
|
| 40-60
| 6-8
|
| 60-100
| 7-10
|
| 100-200
| 8-12
|
| > 200
| 10-15
|
Более точная величина К определяется по формуле 1 Стерджеса (1926)
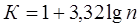 (1)
(1)
или по формуле 2 Брукса и Карузерса (1963)
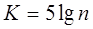 (2)
(2)
В тех случаях, когда по вариационному ряду вычисляются численные характеристики (средняя, дисперсии) следует выделять 15-20 классов, независимо от числа наблюдений (Юла, Кендэл, 1960).
Вариационный ряд и его графическое изображение
После распределения всех вариант по классам получаются ряды, которые называются вариационными. По вариационному ряду можно судить о границах (min и max) и о характере вариации. Класс, обладающий наибольшей частотой называется модальным, значения же крайних классов – лимитами или пределами.
Всякий вариационный ряд можно изобразить графически. Существует несколько способов изображения конкретных вариационных рядов. Первый из них применяется при дискретной (прерывистой) вариации, но в том случае, если классы намечены по отдельным значениям вариант, носит название полигона распределения. При построении полигонов нужно всегда доводить их справа и слева до нулевых, то есть до тех соседних классов, в которых уже нет ни одной варианты.
В том случае, когда частота встречаемости выражается не перпендикуляром, а столбиком, основанием которого являются значения класса, график носит название гистограммы или номограммы (рис. 3).
Графическое изображение вариационного ряда это показатель более совершенного анализа.
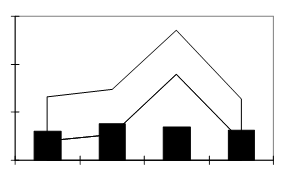
Рис. 3. Графическое изображение вариационных рядов: линиями или столбиками (перпендикулярами)
Основные характеристики вариационных рядов
Каждый вариационный ряд и его графическое изображение – это как бы «сгущение» исходного фактического материала, превращение его в наглядную форму. Однако этого недостаточно. Очень важно получить характеристики совокупности, которые были бы выражены цифровыми показателями. С их помощью можно сравнивать различные ряды. Одним из простейших способов количественной характеристики вариационного ряда является указание на его размах, то есть на верхнюю и нижнюю границы, которые обычно называются лимитами. Лимиты не указывают на то, как распределяются по изучаемому признаку отдельные члены совокупности. Вот почему для характеристики членов совокупности нужны такие показатели, которые отражали бы свойства всех ее членов.
Две группы показателей для характеристики вариационных рядов
Вариационные ряды могут различаться:
а) по тому значению признака, вокруг которого концентрируется большинство вариант. Это значение признака отражает как бы уровень развития признака в данной совокупности, или иначе центральную тенденцию ряда, то есть типичное для ряда;
б) по степени вариации вокруг уровня, по степени отклонения от центральной тенденции ряда.
Соответственно этому статистические показатели разделяются на две группы: показатели, которые характеризуют центральную тенденцию ряда, или уровень ряда, и показатели, измеряющие степень вариации.
К первой группе относятся различные средние величины: мода, медиана, средняя арифметическая, средняя геометрическая. Ко второй: вариационный размах, среднее абсолютное отклонение, среднее квадратическое отклонение, варианса (или дисперсия), коэффициенты асимметрии и вариации.
Мода и медиана. Например, в вариационном ряду массы леща 47 экз. из 100 имели массу 1200 г, то есть класс 1200 г обладал наибольшей частотой. Такой класс был назван модальным. Значение же модального класса называют модой и обозначают символом Μо. Величина моды является как бы типичной для всей совокупности. В случае же, когда модальным является класс 1200-1400, то есть охватывает несколько значений вариант, то для его характеристики необходимо вычислить среднее значение класса. Оно равно 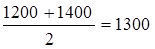 . В таком случае М = 1300.
. В таком случае М = 1300.
К числу средних величин относится также медиана. Медиана – это среднее значение варианты, находящееся точно в середине ряда.
Чтобы найти такую варианту, надо сначала расположить все варианты по порядку от минимальных до максимальных значений. Такое расположение вариант называется ранжировкой. В нечетном ряду, состоящем из 25 вариант, медиана будет 13 по счету, при четном числе вариант берут значения двух соседних срединных вариант и сумму их делят на два.
Модой и медианой пользуются, когда данные не являются чисто количественными и не могут быть представлены в виде точного вариационного ряда, например, степень наполнения желудков или ожирение, выраженные в баллах. Тогда мода и медиана могут достаточно хорошо характеризовать типичное в совокупности.
Обычно же, когда изучаемая совокупность, достаточно однородна и вариации внутри нее чисто количественные, выгоднее пользоваться другими средними величинами.
Средняя арифметическая и ее свойства
Нахождение средней арифметической – это, в сущности, замена индивидуальных варьирующих значений признаков отдельных членов совокупности некоторой уравненной величиной при сохранении основных свойств всех членов совокупности. Этому условию в наибольшей степени удовлетворяет, так называемая средняя арифметическая, обозначаемая через символ М. Она вычисляется по формуле 3:
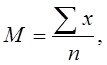 (3)
(3)
где М – средняя арифметическая;
∑ – знак суммирования;
х – результат измерения признака у каждого объекта;
п – число объектов в группе.
Применение более сложных формул для вычисления средней арифметической необходимо только для облегчения счетной работы при отсутствии достаточной счетной техники. При этом надо помнить, что облегчение расчетов получается за счет небольшого практически малозаметного снижения точности определения средней.
Если нет счетной техники и требуется усреднить признак в многочисленной группе, когда непосредственное сложение становится затруднительным, применяется обходный путь расчета средней арифметической величины – через составление вариационного ряда, например, методом произведений.
Измерение вариации, вариационный размах и средние отклонения
Средняя арифметическая указывает на то, какое значение признака наиболее характерно для данной совокупности. Но сама по себе она еще недостаточна для характеристики совокупности, так как главной особенностью ее является наличие разнообразия между ее членами, то есть вариации. Если бы не было вариаций, то информацию можно было бы получить по одному члену совокупности.
Учет вариации того или иного признака имеет чрезвычайное значение. Определение вариационного размаха, то есть разницы между минимальным и максимальным значениями вариант может указать на степень вариации, но этого недостаточно, так как крайние величины в рядах не очень устойчивы и легко сдвигаются, во вторых, распределение отдельных вариант в рядах может быть различным.
Вот почему для характеристики различий между отдельными значениями случайной переменной, например, длина рыбы, нужен такой показатель, который обобщал бы колеблемость всех вариант. Для этого надо сравнивать варианты или друг с другой или с какой-то постоянной величиной. В качестве последней лучше всего взять среднеарифметическую.
Раньше для получения этого показателя, носящего названия среднего отклонения и среднего абсолютного отклонения, брали сумму отклонения средних вариант, то есть разницу между значениями отдельных вариант каждой варианты и средней арифметической и делили ее на n то есть получали величину 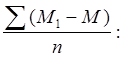
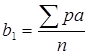 (4).
(4).
Однако оказалось, что среднее отклонение не улавливает истинной закономерности вариации, то есть рассеивания вариант в совокупности или в вариационном ряду вокруг средней арифметической.
Более совершенными показателями, характеризующими вариацию, является средний квадрат отклонения от средней арифметической, иначе называемый вариансой, среднеквадратическим отклонением, стандартным отклонением (5).
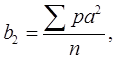 (5)
(5)
Вариансу обозначают σ2 (греческая буква сигма), а среднее квадратическое отклонение σ (6).
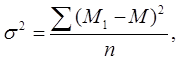 тогда
тогда
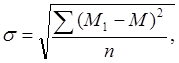 или
или
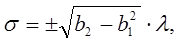 (6)
(6)
где λ – классовый промежуток.
Пример вычисления статистических характеристик
| Размерный ряд
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| n
|
|
|
|
|
|
|
|
|
| p
| 1 0 1 2 1 3 1 3 1 3 1 2
|
|
| 23,1
|
| a
| -6 -5 -4 -3 -2 -1 +1 +2 +3 +4 +5
|
|
| 22,2
|
| pa
| -6 0 -4 -6 -2 -3 3 2 9 4 10
|
|
| 21,1
|
| a2
| 36 25 16 9 4 1 1 4 9 16 25
|
|
| 23,5
|
| pa2
| 36 0 16 18 4 3 3 4 27 16 50
|
|
| 20,5
|
|
|
|
|
|
|
|
|
|
|
| А – усл. ср.= 22,5
|
|
|
| 26,3
|
|
|
|
|
|
|
|
|
|
|
| Мср.=А+b1 = 22,5+0,35=22,85
|
| 21,0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 27,1
|
|
|
|
|
|
|
|
| 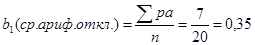
|
| 21,5
|
|
|
|
|
|
|
|
|
| 25,6
|
|
|
|
|
|
|
|
|
| 23,4
|
|
|
|
|
|
|
|
| 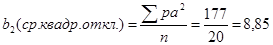
|
| 25,0
|
|
|
|
|
|
|
|
|
| 16,8
|
|
|
|
|
|
|
|
|
| 25,2
|
|
|
|
|
|
|
|
| 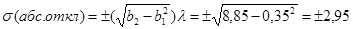
|
| 19,3
|
|
|
|
|
|
|
|
|
| 24,7
|
|
|
|
|
|
|
|
|
| 19,6
|
|
|
|
|
|
|
|
| 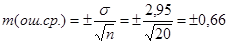
|
| 25,4
|
|
|
|
|
|
|
|
|
| 18,6
|
|
|
|
|
|
|
|
|
| 27,2
|
|
|
|
|
|
|
|
| 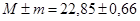
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После извлечения корня квадратного получаются значения со знаком плюс или минус; обычно берут только положительное значение.
Оценка достоверности собранного материала
Проблема достоверности занимает видное место в статистической теории.
Напомним, что генеральная совокупность – это вся подлежащая изучению совокупность данных объектов. В пределе она рассматривается как состоящая из бесконечно большого количества отдельных единиц. Та часть совокупности, которая подвергается исследованию, называется выборочной совокупностью или просто выборкой. Оба типа совокупностей характеризуются одинаковыми закономерностями и для их характеристики могут быть вычислены статистические показатели: средняя арифметическая и средне квадратическое отклонение.
Оказывается, что отдельные значения среднеарифметических выборок варьируют вокруг среднеарифметической генеральной совокупности М (мю). Вариация же выборочных средних вокруг М (мю) может быть измерена своим средним квадратическим отклонением, своей сигмой. Эта сигма получила название средней ошибки или среднеквадратической ошибки. Именно она указывает на степень близости М и m.
Средняя ошибка для М может быть вычислена по формуле 7:
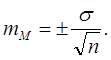 (7)
(7)
Она является ни чем иным, как среднеквадратическим отклонением вариационного ряда, составленного из отдельных значений М.
Для изучения закономерностей вариации при нормальном распределении широко пользуются так называемым нормированным отклонением, которое обозначается буквой t, и представляет собой отклонение той или другой варианты от средней арифметической, выраженное в сигмах:
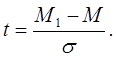 (8)
(8)
Размещение вариант в вариационном ряду при нормальном распределении характеризуется определенными закономерностями.
Дело в том, что в нормальной кривой отклонения от средней арифметической укладываются в 6 сигм: 3 сигмы вправо и 3 сигмы влево от средней.
Для установления разницы между средними арифметическими двух рядов надо воспользоваться нормированным отклонением t, которое примет следующую формулу 9:
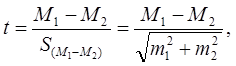 (9)
(9)
где числителем является разница между средними арифметическими двух групп (знак разницы не имеет значения), ее сокращенно обозначают буквой d. В знаменателе же средняя ошибка этой разницы, т.е. 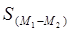 , или более сокращенно Sd. Тогда:
, или более сокращенно Sd. Тогда:
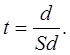 (10)
(10)
Вероятность достоверности находится либо по таблицам нормального интеграла вероятности, при отсутствии таблиц можно исходить из правила 3-х сигм: если разница превышает свою ошибку почти в 3 раза, она достоверна с вероятностью не менее 0,99. Но в таком высоком значении t нет надобности. Если n >30, то t =2,58 гарантирует достоверность разницы с вероятностью 0,99, или ошибка не больше 3-х сигм.
Достоверность выборочной разницы измеряется особым показателем, который можно назвать критерием достоверности разницы.
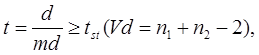 (11)
(11)
где d = M 1- M 2 – разность выборочных средних;
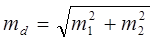 – ошибка выборочной разности;
– ошибка выборочной разности;
tst – стандартное значение критерия, определяемое по таблицам критериев Стьюдента (табл. 19), для заданного порога вероятности безошибочных прогнозов (0,95; 0,99; 0,999), в зависимости от числа степеней свободы n 1, n 2 – численности сравниваемых выборок
Vd = n 1 + n 2 – 2 – число степеней свободы для разности двух средних.
При использовании критерия достоверности разности возможны два случая:
1) td ≥ tst – полученный в исследовании критерий достоверности равен или превышает стандартное значение критерия, найденное по Стьюденту. В этом случае разность достоверна с определенной надежностью, т.е. соответствует по знаку генеральной разности. Если эмпирический критерий равен или превышает первый порог, он подчеркивается одной чертой, если равен или превышает второй и третий пороги, он подчеркивается двумя или тремя чертами.
2) td < tst – полученный критерий достоверности меньше стандартного значения для минимального или требуемого порога вероятности. В этом случае разность не достоверна, что значит:
а) по выборочной разности нельзя сделать никакой оценки генеральной разности;
б) осталось невыясненным, какая из двух средних больше;
в) осталось недоказанным как наличие, так и отсутствие различия между генеральными средними.
За минимальный порог достоверности в подавляющем большинстве принимается первый порог, соответствующий вероятности безошибочных прогнозов β1 – 0,95. Эмпирический критерий при недостаточной разнице подчеркивается волнистой чертой.
Таблица 19
Критические значения t критерия Стьюдента для трех уровней значимости (а)
и чисел степеней свободы (K)
Числа степеней свободы 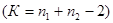
| Уровни значимости, %
| Числа степеней свободы 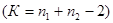
| Уровни значимости, %
|
|
|
| 0,1
|
|
| 0,1
|
|
| 12,71
| 63,66
| -
|
| 2,10
| 2,88
| 3,92
|
|
| 4,30
| 9,92
| 31,60
|
| 2,09
| 2,86
| 3,88
|
|
| 3,18
| 5,84
| 12,92
|
| 2,09
| 2,85
| 3,85
|
|
| 2,78
| 4,60
| 8,61
|
| 2,08
| 2,83
| 3,82
|
|
| 2,57
| 4,03
| 6,87
|
| 2,07
| 2,82
| 3,79
|
|
| 2,45
| 3,71
| 5,96
|
| 2,07
| 2,81
| 3,77
|
|
| 2,37
| 3,50
| 5,41
|
| 2,06
| 2,80
| 3,75
|
|
| 2,31
| 3,36
| 5,04
|
| 2,06
| 2,79
| 3,73
|
|
| 2,26
| 3,25
| 4,78
|
| 2,06
| 2,78
| 3,71
|
|
| 2,23
| 3,17
| 4,59
|
| 2,05
| 2,77
| 3,69
|
|
| 2,20
| 3,11
| 4,44
|
| 2,05
| 2,76
| 3,67
|
|
| 2,18
| 3,05
| 4,32
|
| 2,05
| 2,76
| 3,66
|
|
| 2,16
| 3,01
| 4,22
|
| 2,04
| 2,75
| 3,65
|
|
| 2,14
| 2,98
| 4,14
|
| 2,02
| 2,70
| 3,55
|
|
| 2,13
| 2,95
| 4,07
|
| 2,00
| 2,66
| 3,46
|
|
| 2,12
| 2,92
| 4,02
|
| 1,98
| 2,62
| 3,37
|
|
| 2,11
| 2,90
| 3,97
| ∞
| 1,96
| 2,58
| 3,29
|
| Р
| 0,05
| 0,01
| 0,001
|
| 0,05
| 0,01
| 0,001
|
(Цитировано по П.Ф. Рокицкому (1961), И.Ф. Правдину (1966), Г.Ф. Лакину (1980))
О некоторых требованиях к средним в рыбохозяйственных исследованиях
(По С.В. Козлитиной, 1969)
Средняя величина может быть надежным и объективным показателем лишь тогда, когда при ее вычислении соблюдаются определенные правила.
К числу основных из них можно отнести следующие:
1) Однородность изучаемого материала, которая достигается путем использования данных, относящихся к районам или водоемам с незначительными пространственными контрастами, в случае значительных контрастов необходимо выделять районы с характерными концепциями.
2) Исключение систематических ошибок, к которым относятся в основном инструментальные ошибки, влияющие более или менее одинаково на весь ряд наблюдений. Устранить эти ошибки можно только путем введения поправок. Например при определении численности рыб в море, вводится поправка на уловистость орудий лова.
3) Грубые ошибки. Поскольку все измерения представляют собой ограниченную выборку из генеральной совокупности и в выборку может попасть величина, частота которой невелика. И хотя ее появление возможно принимать в расчеты наравне со всеми остальными величинами неправомерно, так как вероятность такой величины близка к нулю. Обычно применяют критерий, позволяющий установить принадлежность случайной величины к рассматриваемой совокупности; это правило трех сигм. Если известна величина и среднеквадратическое отклонение одного измерения, то находят приближенную ошибку каждого измерения, то есть отклонения измеренной величины от средней 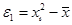 . Обычно считают маловероятным, чтобы модуль ошибки превышал три сигмы.
. Обычно считают маловероятным, чтобы модуль ошибки превышал три сигмы.
Поэтому если найдется какое-нибудь 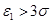 , то соответствующее измерение считается содержащим грубую ошибку и отбрасывается.
, то соответствующее измерение считается содержащим грубую ошибку и отбрасывается.
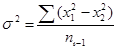 (12)
(12)
4) существуют случайные ошибки, исключить которые невозможно, но можно учесть как погрешность наблюдения, так как случайные ошибки подчиняются нормальному закону распределения. На практике процесс обработки считается законченным, если подсчитана средняя квадратическая ошибка среднего арифметического (13)
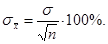 (13)
(13)
При записи среднего арифметического принято указывать среднеквадратическую ошибку, обычно выражаемую в процентах.
Расчеты по выше указанным методам и формулам можно производить с помощью вычислительной техники (ЭВМ), используя методы современного программирования (листинг 1).
Листинг 1. Пример расчета средней с помощью языка программирования Pascal
Program Statistica;
var A: array [1..100] of real;
Y,S,Sa,Sko,D,Osa,Kv: real;
i,N: integer;
begin
writeln('Расчет статистических характеристик ряда');
write('Количество данных: '); readln(N);
writeln('Введите данные:');
writeln('N п/п данные');
for i:=1 to N do begin
write(i:3,' ');
readln(A[i])
end;
S:=0;
for i:=1 to M do S:=S+A[i];
Sa:=S/N;
S:=0;
for i:=1 to N do S:=S+sqr(A[i]-Sa);
D:=S/N;
Sko:=sqrt(D);
Osa:=Sko/sqrt(N);
Kv:=Sko/Sa;
writeln('Среднее арифметическое=',SA:8:1);
writeln('Ошибка средней=',Osa:8:1);
writeln('Дисперсия=',D:8:1);
writeln('Среднее квадратическое отклонение=',Sko:8:1);
writeln('Коэффициент вариации=',Kv:8:1);
readln
end.
Контрольные вопросы и задания
1. Дать понятие моде и медиане, средней арифметической и среднегеометрической величинам.
2. Измерение вариаций, вариационного размаха и средних отклонений: вариансы, среднеквадратического отклонения и стандартного отклонения (сигмы).
3. Оценка достоверности собранного материала, критерии достоверности.
4. Ошибки (систематические, грубые, случайные) при выполнении вариационно-статистических расчетах.



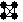 .
.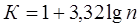 (1)
(1)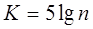 (2)
(2)
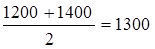 . В таком случае М = 1300.
. В таком случае М = 1300.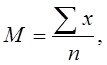 (3)
(3)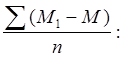
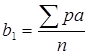 (4).
(4).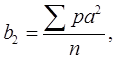 (5)
(5)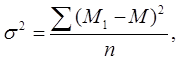 тогда
тогда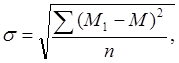 или
или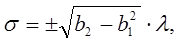 (6)
(6)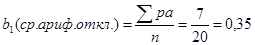
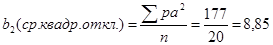
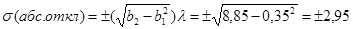
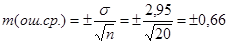
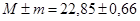
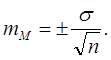 (7)
(7)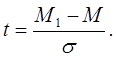 (8)
(8)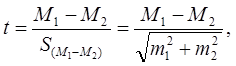 (9)
(9)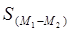 , или более сокращенно Sd. Тогда:
, или более сокращенно Sd. Тогда: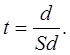 (10)
(10)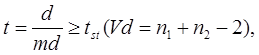 (11)
(11)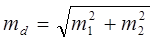 – ошибка выборочной разности;
– ошибка выборочной разности;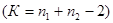
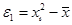 . Обычно считают маловероятным, чтобы модуль ошибки превышал три сигмы.
. Обычно считают маловероятным, чтобы модуль ошибки превышал три сигмы.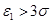 , то соответствующее измерение считается содержащим грубую ошибку и отбрасывается.
, то соответствующее измерение считается содержащим грубую ошибку и отбрасывается.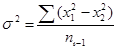 (12)
(12)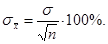 (13)
(13)


