МОДУЛЬ 1
Основы теории разностных схем
ОГЛАВЛЕНИЕ
МОДУЛЬ 1. ОСНОВЫ ТЕОРИИ РАЗНОСТНЫХ СХЕМ………………………………..………..1
1.1. Комплексная цель модуля……………………………………......……………...1
1.2. Введение………………………………………………………………………...1
1.3. Сетки и сеточные функции. Вводные понятия…………………………………2
1.4. Построение разностных схем………………………………………………… 5
1.5. Принцип максимума и следствия из него…………………………………......50
1.6. Энергетический метод исследования устойчивости……………………….... 74
1.7. Корректность операторно-разностных уравнений…………………………...91
1.8. Введение в метод конечных элементов…………………………………….141 Заключение…………………………………………………………………...191
1.10 Проектное задание………………………………………………………….192
1.11Тест рубежного контроля……………………………………………………199
Основным предметом данного модуля является построение и исследование дискретных моделей для задач математической физики. В качестве дискретных моделей рассматриваются конечно-разностные и конечно-элементные схемы.
Комплексная цель модуля
Изучить современные методы численного решения задач математической физики. Сформировать навыки построения вычислительных алгоритмов для решения базовых задач численного анализа и теоретического исследования основных свойств алгоритма.
Введение
Теория разностных схем представляет один из основных разделов
современной вычислительной математики.
В модуле отмечены основные подходы к построению дискретных аналогов
краевых задач с различными граничными условиями.
Каждый содержательный раздел модуля начинается с общих сведений о методах и способах решаемых в нем задач и заканчивается набором упражнений, закрепляющих знание теории.
В первом разделе даются основные понятия модуля.
Во втором разделе на примере консервативной схемы, построенной интегро-
интерполяционным методом для обыкновенного дифференциального уравнения
второго порядка, исследуются вопросы порядка аппроксимации, устойчивости и
сходимости. Здесь же рассматриваются свойства разностных операторов,
использующиеся в других разделах модуля.
В третьем разделе доказывается принцип максимума для разностных схем,
записанных в канонической форме. Принцип максимума применяется к
исследованию сходимости разностной аппроксимации задачи Дирихле. Приводятся
примеры применения принципа максимума к другим стационарным и
нестационарным задачам.
Четвертый и пятый разделы посвящены исследованию устойчивости и
корректности операторно-разностных уравнений. Разностные схемы определяются
как операторные уравнения с операторами, действующими в евклидовом
пространстве. Условия устойчивости формулируются в виде операторных
неравенств.
В последнем заключительном разделе модуля для построения приближенного
решения применяется метод конечных элементов. Дается общее описание метода и
приводится пример построения и исследования конечно-элементной схемы для
первой краевой задачи обыкновенного дифференциального уравнения второго порядка.
Построение разностных схем
Разностные операторы и их свойства
1. Разностные тождества
Связь аппроксимации, устойчивости, сходимости
Схема с весами
Рассмотрим задачу для уравнения теплопроводности с постоянными коэффициентами.
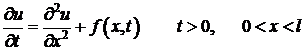 . (1)
. (1)
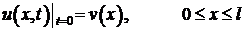 . (2)
. (2)
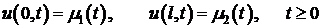 . (3)
. (3)
Согласование начальных и граничных условий:
 .
.
Для уравнения теплопроводности схема с весами имеет вид:

 . (4)
. (4)
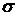 - числовой параметр:
- числовой параметр: 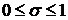
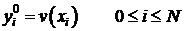 . (5)
. (5)
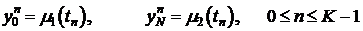 . (6)
. (6)
Согласование начальных и граничных условий:
 . (7)
. (7)
Получим задачу для погрешности решения.
Подставим
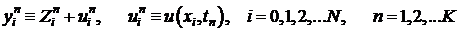
в (4, 5, 6).
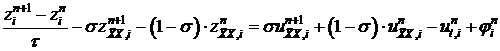 . (8)
. (8)
 . (9)
. (9)
 . (10)
. (10)
Задача (8-10) поставлена.
Задача (8) по своей структуре (по результату действия оператора левой части уравнения) аналогична задаче (4), если (4) переписать в виде:
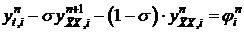 . (4′)
. (4′)
Отличия возникли в правых частях у задачи (4′) это 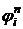 , у (8) – погрешность аппроксимации разностных уравнений (4) на решении непрерывной задачи (1, 2, 3).
, у (8) – погрешность аппроксимации разностных уравнений (4) на решении непрерывной задачи (1, 2, 3).
Исследуем эту погрешность аппроксимации, предполагая, что разностная схема (4, 5, 6) устойчива.
______________________________________________________________
‼ Исследовать условия устойчивости для задачи (4 - 6) методом гармоник.
______________________________________________________________
Исследуем погрешность аппроксимации.
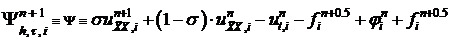 . (11)
. (11)
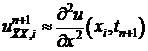

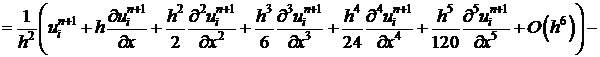
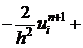
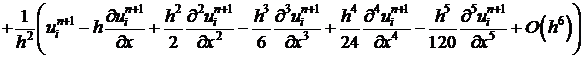
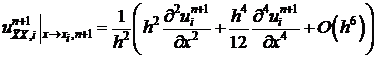 .
.
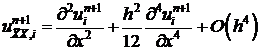 . (12)
. (12)
Аналогично:
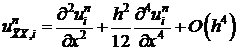 . (13)
. (13)
Подставим (12), (13) в (11).
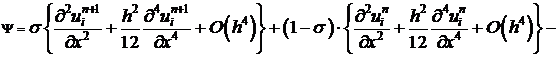
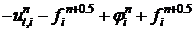 . (14)
. (14)
Разложим функции, стоящие в фигурных скобках по переменной 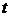 в окрестности
в окрестности 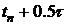 в ряд.
в ряд.
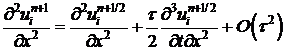 . (15)
. (15)
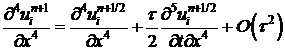 . (16)
. (16)
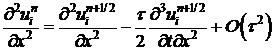 . (17)
. (17)
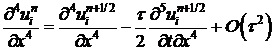 . (18)
. (18)
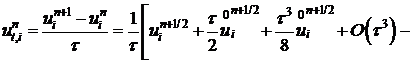
 .
.
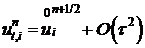 . (19)
. (19)
Подставим (15)-(19) в (14).
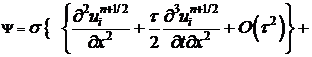
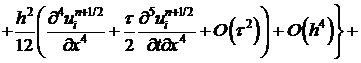

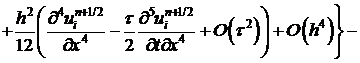
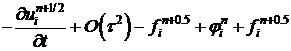 .
.
Пусть 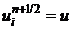 ;
; 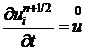

 .
. 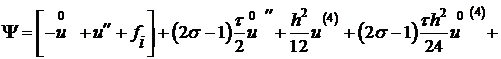
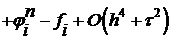 . (20)
. (20)
Из полученного представления видно, что при 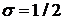 погрешность аппроксимации
погрешность аппроксимации
 .
.
В частности, если 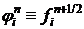 , то
, то 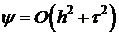 - симметричная схема с весами.
- симметричная схема с весами.
Если 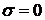 имеем явную схему, для которой
имеем явную схему, для которой
 .
.
Если  имеем неявную схему, для которой
имеем неявную схему, для которой 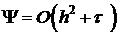 .
.
Воспользуемся следующим равенством:
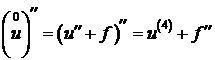 . (21)
. (21)
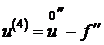 (22)
(22)
подставим (22) в (20):
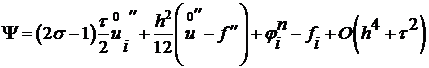 .
.
Преобразуя выражение получаем:
 .
.
Будем считать, что
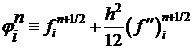 .
.
(23)
Выберем итерационный параметр 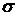 так, чтобы первое слагаемое обращалось в ноль.
так, чтобы первое слагаемое обращалось в ноль.
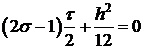 .
.
Следовательно,
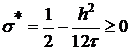 .
.
При таком итерационном параметре мы имеем схему повышенного порядка аппроксимации.
______________________________________________________________
‼ Существуют ли такие значения итерационного параметра 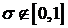 , при которых погрешность аппроксимации
, при которых погрешность аппроксимации 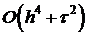 ?
?
______________________________________________________________
Были рассмотрены двухслойные разностные схемы. Для уравнений гиперболического типа используют трехслойные разностные схемы.
Примеры трехслойных разностные схем для уравнения теплопроводности
Возникает идея повысить точность аппроксимации для уравнения теплопроводности до 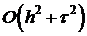 за счет использования трехслойных схем.
за счет использования трехслойных схем.
Минимальный шаблон, обеспечивающий такую точность включает в себя точки: 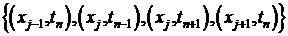 .
.
Так как аппроксимация граничных условий очевидна, то займемся разностными аналогами уравнения (1).
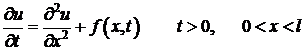 . (1)
. (1)
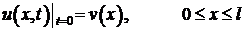 . (2)
. (2)
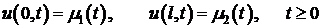 . (3)
. (3)
Согласование начальных и граничных условий:
 .
.
1) абсолютно не устойчивая схема.
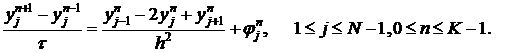
Схема имеет точность 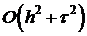 .
.
_______________________________________________________________________
‼ Методом гармоник показать, что данная схема неустойчива.
_______________________________________________________________________
Рассмотрим формальную замену
 .
.
С учетом ее рассмотрим схему вида:
2) 

_______________________________________________________________________
1. ‼ Методом гармоник показать, что данная схема неустойчива;
2. ‼ получить оценку 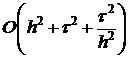 ;
;
3. ‼ построить непрерывный аналог данной схемы сохранив члены имеющие порядок малости  .
.
_______________________________________________________________________
Принцип максимума
Напомним определение связности сетки.
Опр.
Сетка  называется связной, если
называется связной, если 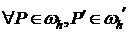 найдется множество узлов:
найдется множество узлов: 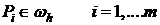 , что выполняется:
, что выполняется:
(7) 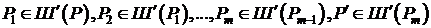 .
.
Некоторые из этих точек, попадающих в окрестность, могут быть и граничными.
Теорема 1. Принцип максимума.
Пусть для сеточной функции  не являющейся тождественной константой для любых
не являющейся тождественной константой для любых 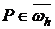 выполняется:
выполняется:
1. 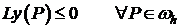 , (считаем, что
, (считаем, что 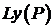 сеточный оператор с коэффициентами, удовлетворяющими условию (5), а сетка
сеточный оператор с коэффициентами, удовлетворяющими условию (5), а сетка 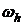 -связная), тогда сеточная функция
-связная), тогда сеточная функция  не может достигать наибольшего положительного значения во внутренних узлах сетки.
не может достигать наибольшего положительного значения во внутренних узлах сетки.
2.  , тогда сеточная функция
, тогда сеточная функция  не может достигать наименьшего отрицательного значения во внутренних узлах сетки.
не может достигать наименьшего отрицательного значения во внутренних узлах сетки.
Доказательство.
Предположим противное: существует такая точка  . Тогда найдется хотя бы одна точка
. Тогда найдется хотя бы одна точка  .
.
Так как  , среди всех
, среди всех  зафиксируем
зафиксируем 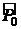 .
.
В силу связанности сетки существует конечное множество узлов:
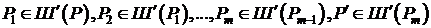 .
.
Рассмотрим уравнение (3′) в точке 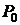 .
.
(8)  .
.
В силу (5, 6):  в силу (5):
в силу (5):  .
.
Если использовать «сильное» определение, то точка 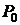 - точка в которой сеточная функция достигает наибольшего значения, то
- точка в которой сеточная функция достигает наибольшего значения, то 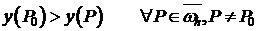 , то неравенство (8) не выполняется, т.к.
, то неравенство (8) не выполняется, т.к. 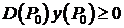 , а
, а  .
.
Более интересным является применение другого «слабого» определения наибольшего значения: 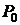 - точка в которой сеточная функция достигает своего наибольшего значения, то
- точка в которой сеточная функция достигает своего наибольшего значения, то  при условии, что найдется хотя бы одна точка
при условии, что найдется хотя бы одна точка  .
.
Будем ориентироваться на это более содержательное определение.
Тогда 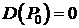 ,
,  , следовательно
, следовательно 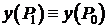 . Выберем точку
. Выберем точку 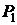 в качестве центра шаблона.
в качестве центра шаблона.
Имеем:  .
.
Так как 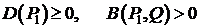 , то
, то  . Следовательно,
. Следовательно, 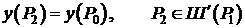 .
.
Аналогично проделав для остальных узлов неравенства (3′) тоже самое, приходим к цепочке равенств:  .
.
Теперь рассмотрим левую часть неравенства (8).
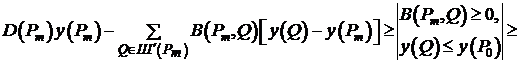
 .
.
Полученное неравенство противоречит предположению 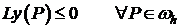 .
.
Следствие 1.
Пусть выполнены условия предыдущей теоремы, кроме одного  может быть тождественной константой на сетке.
может быть тождественной константой на сетке.
Сеточная функция  , заданная
, заданная  неотрицательна на границе
неотрицательна на границе  , т.е.
, т.е. 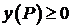 и имеет место
и имеет место 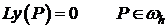 .
.
Тогда функция 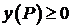
 .
.
Доказательство.
1. Пусть 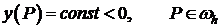 ;
;
2. 
Рассмотрим первый пункт.
Выберем в качестве точки 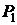 так называемый приграничный узел, т.е.
так называемый приграничный узел, т.е. 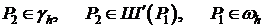 .
.
Рассмотрим уравнение (3′) в точке 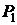 .
.
(9) 
1) 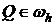 , тогда
, тогда  , т.к.
, т.к. 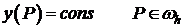 .
.
2) 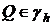 , тогда
, тогда  ,
, 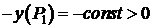
 ,
,  .
.
Отсюда вытекает, что левая часть (9) отрицательна, что противоречит условию, что  .
.
Рассмотрим второй пункт.
Пусть существует точка  , тогда в силу предыдущей теоремы 1
, тогда в силу предыдущей теоремы 1  , следует, что нет такой точки
, следует, что нет такой точки  .
.
Если точка 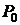 не единственная точка сетки, в которой значение функции отрицательно, то среди всех этих точек
не единственная точка сетки, в которой значение функции отрицательно, то среди всех этих точек  следует выбрать такую точку, что
следует выбрать такую точку, что 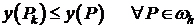 , которая удовлетворяет неравенству. Если
, которая удовлетворяет неравенству. Если 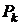 не одна, то выбирается любая.
не одна, то выбирается любая.
Следствие 2.
Однородное уравнение  с однородными граничными условиями
с однородными граничными условиями  ,
, 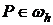 ,
, 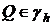 имеет только тривиальное решение.
имеет только тривиальное решение.
Доказательство.
Из теоремы
1) 
 , если
, если 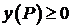 ;
;
2) 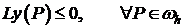
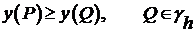 , если
, если 
Из 1) и 2) следует, что  и
и 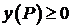 , следовательно
, следовательно  .
.
Следствие 3.
Исходное сеточное уравнение  при условии, что выполняются ограничения (5), (6), а также сетка связная, имеет единственное решение.
при условии, что выполняются ограничения (5), (6), а также сетка связная, имеет единственное решение.
Это следствие вытекает из известной теоремы алгебры, т.к. соответствующая однородная система 
 имеет тривиальное решение в силу следствия 2, следовательно неоднородная система имеет единственное решение.
имеет тривиальное решение в силу следствия 2, следовательно неоднородная система имеет единственное решение.
Опр.
Сеточное уравнение вида:
(1) 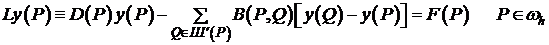
будем называть уравнением, а оператор L – оператором из исходного семейства, если (1) определено во внутренних узлах сетки 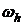 , а
, а 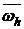 - связное множество относительно шаблона.
- связное множество относительно шаблона.

Теорема 2.
Пусть поставлена задача (I) с уравнением из исходного семейства вида:
(1) 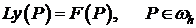 ;
;
(2)  .
.
А также поставлена задача (II):
(3) 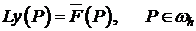 ;
;
(4) 
и выполняются неравенства:
(5′)  ,
, 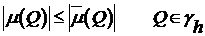
то
( 5) 

Замечание.
Введем обозначение:  ,
,  .
.
Т.о. неравенство (5) можно переписать в виде:  .
.
Задачу (3), (4) называют мажорирующей по отношению к задаче (1), (2).
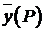 - мажоранта по отношению к
- мажоранта по отношению к  .
.
Доказательство.
Зададим сеточные функции:
(6)  ;
;
(7) 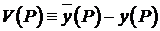 .
.
Нетрудно видеть, что
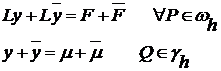
В силу линейности оператора 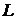 , получаем:
, получаем:
(8) 
(9) 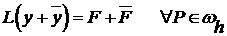 .
.
Задача с учетом (8), (9) может быть записана в виде:
(10)  ;
;
(11)  .
.
Задача (10), (11) удовлетворяет следствию теоремы 1:
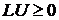 в силу (5′), и граничное условие
в силу (5′), и граничное условие  .
.
Следовательно, 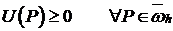 .
.
Аналогично функция  .
.
Вычитая (1) из (3), (2) из (4), и пользуясь линейностью оператора, получаем:

(12) 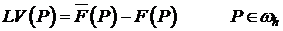 ;
;
(13)  .
.
Таким образом, получаем аналогичную задачу для функции 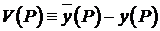 .
.
Итак
(14)  , с другой стороны
, с другой стороны
(15) 
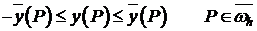
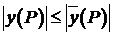 , что и требовалось доказать.
, что и требовалось доказать.
Пример.
Рассмотрим непрерывную задачу:
(1) 
(2) 
Считаем, что уравнение невырожденное.
(3)  .
.
Поскольку коэффициенты постоянны, то
(4)  ,
,
(5)  .
.
Запишем дискретную задачу (4), (5) в канонической форме.
(6) 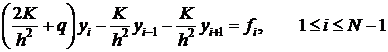
 ,
,
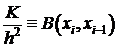 ,
, 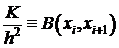 .
.
(7)  .
.
Поставим задачу.
Используя запись (6), (7), ограничения (3) требуется доказать устойчивость задачи (6), (7) по граничным данным и правой части.
Чтобы доказать устойчивость необходимо доказать неравенство:
(8) 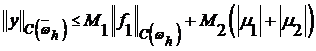 ,
,
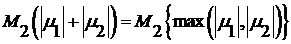 .
.
Рассмотрим две вспомогательные задачи:
I. 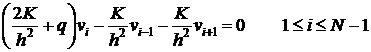
 .
.
Выполняются все условия теоремы сравнения (теорема 2), а именно:
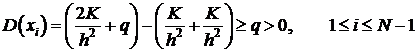 .
.
Для 
 .
.
Следовательно, из теоремы 2, получаем:
(9)  ,
,
 .
.
Неравенство (9) означает, что 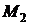 в доказанной оценке (8) равна 1.
в доказанной оценке (8) равна 1.
II.
(10) 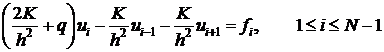
(11)  .
.
Очевидно, все условия теоремы 3 выполняются, следовательно, справедлива оценка:
 .
.
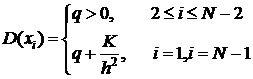 ,
,  .
.
(12)  ,
, 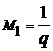 .
.
Из неравенства треугольника и оценок (12), (9) следует оценка:
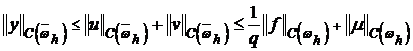 .
.
Полученная оценка может быть использована для доказательства сходимости.
Рассмотрим задачу для погрешности.
Введем погрешность:  .
.
 , подставим в исходную разностную схему (4), (5):
, подставим в исходную разностную схему (4), (5):
(4)  ,
,
(5)  .
.
(13)  ,
,
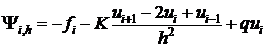
(14)  .
.
По структуре (13), (14) аналогична исходной разностной схеме, отличие состоит лишь в правых частях.

В правой части (13) стоит погрешность аппроксимации исходного разностного дифференциального уравнения разностной схемой на решении задачи.
Ранее было показано, что:
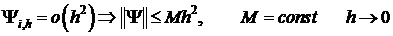
(12′) 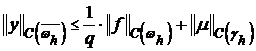 ,
, 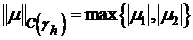 .
.
В соответствии с доказанным и неравенством (12′) получаем,

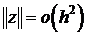 .
.
Примеры решения задач на принцип максимума и следствий из него
Используя принцип максимума, установить достаточное условие устойчивости явной схемы для однородного уравнения теплопроводности.
Пример 1.
(1) 
(2) 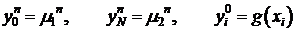 .
.
В канонической форме  .
.
Проверим:
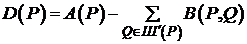
 .
.
Пусть  ,
,  .
.
Следовательно, не существует такого 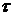 , чтобы
, чтобы  . Следовательно, либо Р неподходящее, либо схема не устойчива.
. Следовательно, либо Р неподходящее, либо схема не устойчива.
Возьмем 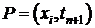 .
.
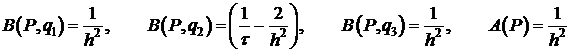 .
.
Схема будет из исходного семейства, если  , т.е.
, т.е. 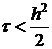 .
.
Замечание.
Интересно отметить, что такое же ограничение будет получено энергетическим методом для исследования устойчивости.
Во внутренних узлах сетки 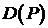 :
:
(3) 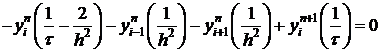 .
.
К полученной задаче применим следствие 4 теоремы 1.
Поэтому 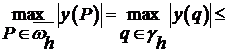 . (*)
. (*)
Границей для данной сеточной задачи является множество узлов: 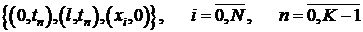 .
.
Предполагается, что условия согласованны.
(*) 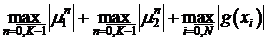 .
.
Второй способ предпочтительнее.
Непосредственно учитываем граничные условия (2) в уравнении (1).
Для 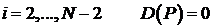 как и ранее.
как и ранее.
В точке 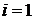 получим (3) в виде:
получим (3) в виде:
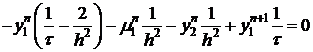
Получим каноническую форму.
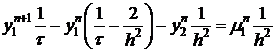 .
.
Уравнение необходимого условия, следовательно,
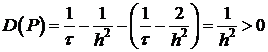 .
.
В точке 
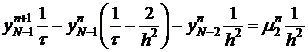 .
.
Следовательно, 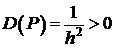 .
.
В точках 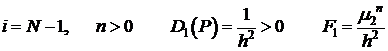 ,
,
 .
.
В точках  имеем:
имеем:
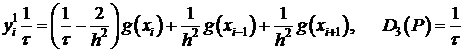 .
.
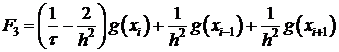 .
.
Формально считаем, что все 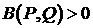 , т.к. окрестность точки Р – пустое множество, т.е. точка Р – единственная.
, т.к. окрестность точки Р – пустое множество, т.е. точка Р – единственная.
В силу теоремы 4
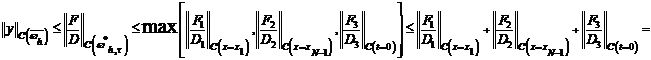
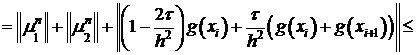
воспользуемся неравенством многоугольников и тем, что 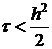 получим
получим 
Пример 2.
(1) 
(2) 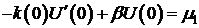
(3) 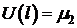 .
.
Так как коэффициенты постоянные, то будем использовать аппроксимацию
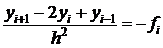 ,
,
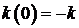 ,
,
 .
.
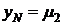
Для повышения порядка можно взять 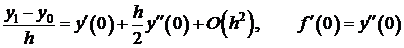 .
.
Разобьем нашу задачу на две, представив решение в виде: 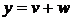 .
.
I. 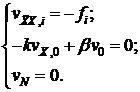
II. 
Разделим (2) на к и переобозначим, получим:
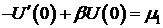
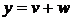 ;
;
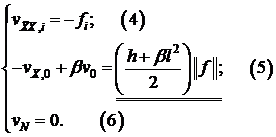
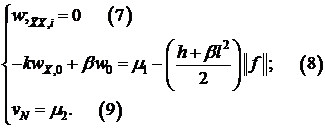
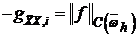 ,
,
 , продифференцируем.
, продифференцируем.
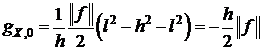 .
.
 .
.
Для задачи (4) – (6) сформулируем вспомогательную задачу:

Последняя задача имеет решение:  .
.
В силу теоремы сравнения
(10)  .
.
Займемся задачей (7), (8), (9), ориентируясь на теорему 4.
Уравнение (7) из исходного семейства
 в котором
в котором  и
и 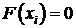 .
.
Займемся точкой  , используя равенство (8).
, используя равенство (8).
 ;
;
 ;
;
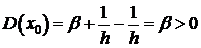 .
.
Таким образом  .
.
Запишем уравнение (7) в 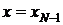 .
.
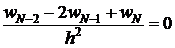 ;
;
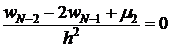 ;
;
 ;
;

Исследование устойчивости закончено, если учесть, что
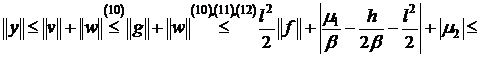 используем неравенство треугольников
используем неравенство треугольников 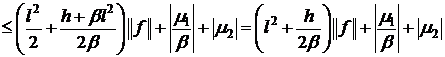 .
.
 .
.
Опр. 1
Оператор  называется сопряженным к
называется сопряженным к 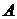 , если
, если 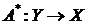 и для любых
и для любых 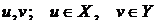 выполняется:
выполняется: 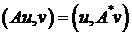 .
.
Если сопряженный оператор  совпадает с исходным оператором, то оператор
совпадает с исходным оператором, то оператор 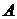 называется самосопряженным.
называется самосопряженным.
Необходимое и достаточное условие самосопряженности оператора
Для самосопряженности оператора  необходимо и достаточно, чтобы в пространстве
необходимо и достаточно, чтобы в пространстве  существовал ортонормированный базис, построенный из собственных векторов оператора
существовал ортонормированный базис, построенный из собственных векторов оператора 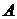 .
.
Будем рассматривать линейные ограниченные операторы.
1) Линейность оператора:
 ,
,  - числа.
- числа.
2) Ограниченность оператора
Что существует такая константа  , что:
, что:  .
.
Пусть 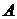 - линейный оператор, действующий
- линейный оператор, действующий 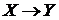 . Для того, чтобы линейный оператор
. Для того, чтобы линейный оператор  существовал и был ограниченным, необходимо и достаточно, чтобы для элемента
существовал и был ограниченным, необходимо и достаточно, чтобы для элемента 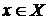 существовала такая константа
существовала такая константа  , не зависящая от
, не зависящая от  , для которой выполнялось неравенство:
, для которой выполнялось неравенство:  . При этом справедлива оценка:
. При этом справедлива оценка: 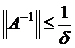 .
.
Далее будем рассматривать линейные ограниченные операторы А, В, С, D, действующие из Н в Н.
Знакоопределенные операторы
Опр. 2
Оператор 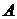 называется неотрицательно определенным, если
называется неотрицательно определенным, если  , положительным, если
, положительным, если  .
.
Опр. 3
Оператор 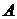 называется положительно определенным, если
называется положительно определенным, если  существует такая константа
существует такая константа  , не зависящая от
, не зависящая от  , такая, что выполняется неравенство:
, такая, что выполняется неравенство: 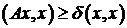 .
.
В случае, когда 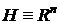 конечномерное пространство, то определения 2 и 3 эквивалентны.
конечномерное пространство, то определения 2 и 3 эквивалентны.
Опр. 4
Оператор 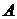 называется кососимметрическим, если
называется кососимметрическим, если  , т.е.
, т.е. 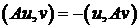 .
.
Любой линейный ограниченный оператор можно представить в виде суммы его кососимметрической и самосопряженной части.
 .
.
Очевидно, что если 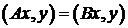 , то
, то  и энергию оператора
и энергию оператора  , можно ввести как отношение неравенств на пространстве линейных операторов.
, можно ввести как отношение неравенств на пространстве линейных операторов.
1) 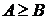 , если
, если  ,
,
2) 
|
|
|



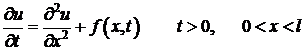 . (1)
. (1)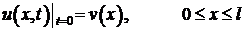 . (2)
. (2)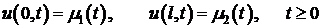 . (3)
. (3) .
.
 . (4)
. (4)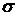 - числовой параметр:
- числовой параметр: 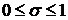
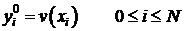 . (5)
. (5)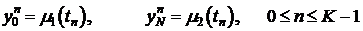 . (6)
. (6) . (7)
. (7)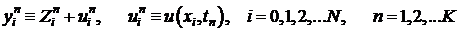
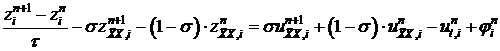 . (8)
. (8) . (9)
. (9) . (10)
. (10)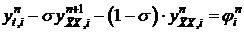 . (4′)
. (4′)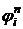 , у (8) – погрешность аппроксимации разностных уравнений (4) на решении непрерывной задачи (1, 2, 3).
, у (8) – погрешность аппроксимации разностных уравнений (4) на решении непрерывной задачи (1, 2, 3).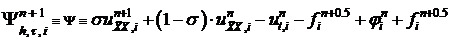 . (11)
. (11)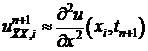

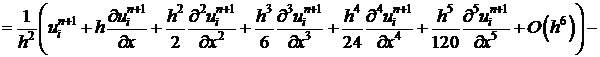
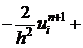
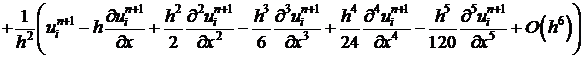
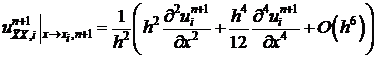 .
.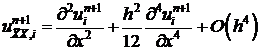 . (12)
. (12)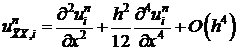 . (13)
. (13)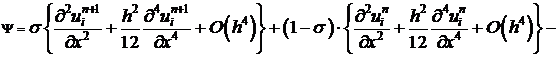
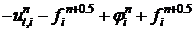 . (14)
. (14)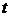 в окрестности
в окрестности 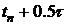 в ряд.
в ряд.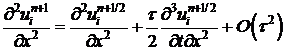 . (15)
. (15)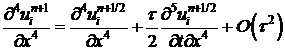 . (16)
. (16)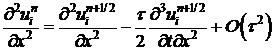 . (17)
. (17)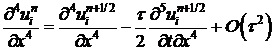 . (18)
. (18)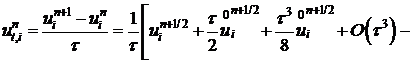
 .
.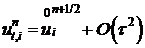 . (19)
. (19)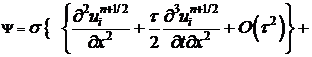
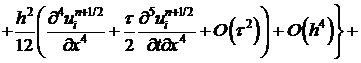

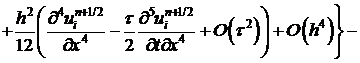
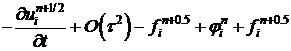 .
.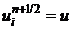 ;
; 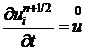

 .
. 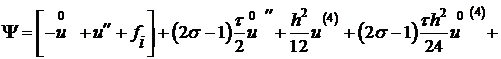
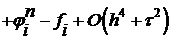 . (20)
. (20)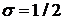 погрешность аппроксимации
погрешность аппроксимации .
.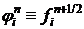 , то
, то 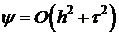 - симметричная схема с весами.
- симметричная схема с весами.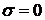 имеем явную схему, для которой
имеем явную схему, для которой .
. имеем неявную схему, для которой
имеем неявную схему, для которой 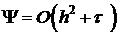 .
.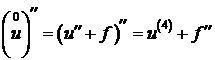 . (21)
. (21)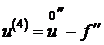 (22)
(22)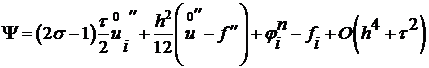 .
. .
. 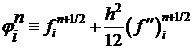 .
.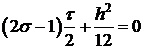 .
.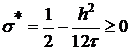 .
.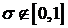 , при которых погрешность аппроксимации
, при которых погрешность аппроксимации 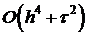 ?
?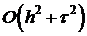 за счет использования трехслойных схем.
за счет использования трехслойных схем.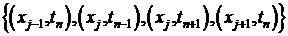 .
.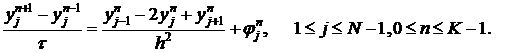
 .
.

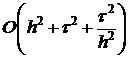 ;
; .
. называется связной, если
называется связной, если 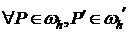 найдется множество узлов:
найдется множество узлов: 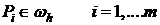 , что выполняется:
, что выполняется: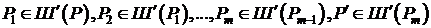 .
. не являющейся тождественной константой для любых
не являющейся тождественной константой для любых 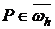 выполняется:
выполняется: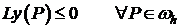 , (считаем, что
, (считаем, что 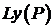 сеточный оператор с коэффициентами, удовлетворяющими условию (5), а сетка
сеточный оператор с коэффициентами, удовлетворяющими условию (5), а сетка 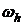 -связная), тогда сеточная функция
-связная), тогда сеточная функция  , тогда сеточная функция
, тогда сеточная функция  . Тогда найдется хотя бы одна точка
. Тогда найдется хотя бы одна точка  .
. , среди всех
, среди всех  зафиксируем
зафиксируем 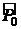 .
.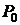 .
. .
. в силу (5):
в силу (5):  .
.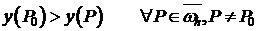 , то неравенство (8) не выполняется, т.к.
, то неравенство (8) не выполняется, т.к. 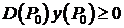 , а
, а  .
. при условии, что найдется хотя бы одна точка
при условии, что найдется хотя бы одна точка 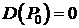 ,
,  , следовательно
, следовательно 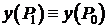 . Выберем точку
. Выберем точку 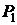 в качестве центра шаблона.
в качестве центра шаблона. .
.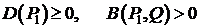 , то
, то  . Следовательно,
. Следовательно, 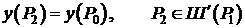 .
. .
.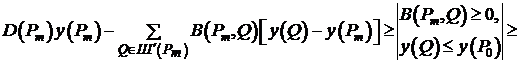
 .
. неотрицательна на границе
неотрицательна на границе  , т.е.
, т.е. 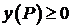 и имеет место
и имеет место 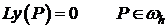 .
.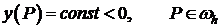 ;
;
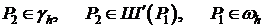 .
.
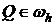 , тогда
, тогда  , т.к.
, т.к. 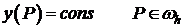 .
.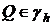 , тогда
, тогда  ,
, 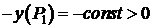
 ,
,  .
. .
. , тогда в силу предыдущей теоремы 1
, тогда в силу предыдущей теоремы 1  следует выбрать такую точку, что
следует выбрать такую точку, что 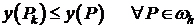 , которая удовлетворяет неравенству. Если
, которая удовлетворяет неравенству. Если 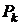 не одна, то выбирается любая.
не одна, то выбирается любая. с однородными граничными условиями
с однородными граничными условиями  ,
, 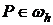 ,
, 
 , если
, если 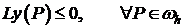
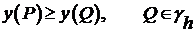 , если
, если 
 при условии, что выполняются ограничения (5), (6), а также сетка связная, имеет единственное решение.
при условии, что выполняются ограничения (5), (6), а также сетка связная, имеет единственное решение.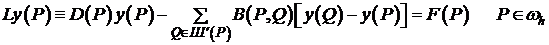
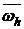 - связное множество относительно шаблона.
- связное множество относительно шаблона.
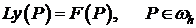 ;
; .
.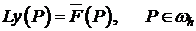 ;
;
 ,
, 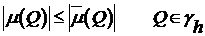


 ,
,  .
. .
.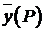 - мажоранта по отношению к
- мажоранта по отношению к  ;
;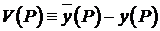 .
.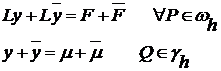
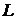 , получаем:
, получаем:
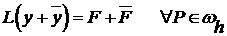 .
. ;
; .
.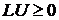 в силу (5′), и граничное условие
в силу (5′), и граничное условие  .
.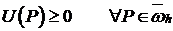 .
. .
.
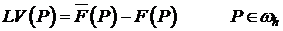 ;
; .
. , с другой стороны
, с другой стороны
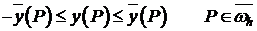
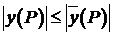 , что и требовалось доказать.
, что и требовалось доказать.

 .
. ,
, .
.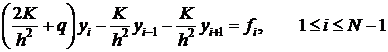
 ,
,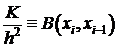 ,
, 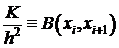 .
.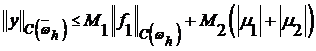 ,
,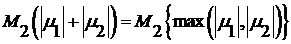 .
.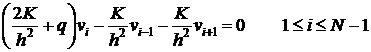
 .
.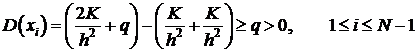 .
.
 .
. ,
, .
.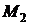 в доказанной оценке (8) равна 1.
в доказанной оценке (8) равна 1.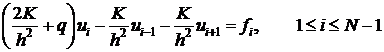
 .
. .
.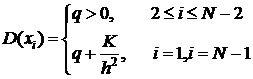 ,
,  .
. ,
, 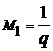 .
.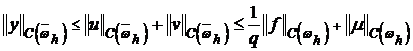 .
. .
. , подставим в исходную разностную схему (4), (5):
, подставим в исходную разностную схему (4), (5): ,
,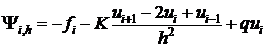
 .
.
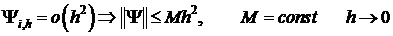
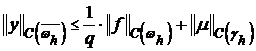 ,
, 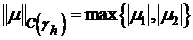 .
.
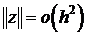 .
.
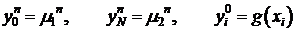 .
. .
.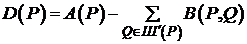
 .
. ,
,  .
.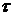 , чтобы
, чтобы  . Следовательно, либо Р неподходящее, либо схема не устойчива.
. Следовательно, либо Р неподходящее, либо схема не устойчива.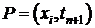 .
.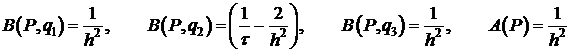 .
. , т.е.
, т.е. 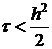 .
.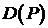 :
: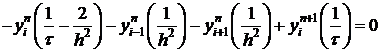 .
.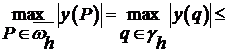 . (*)
. (*)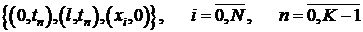 .
.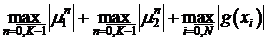 .
.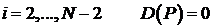 как и ранее.
как и ранее.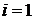 получим (3) в виде:
получим (3) в виде: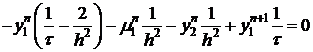
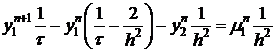 .
.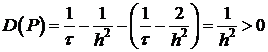 .
.
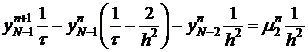 .
.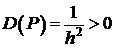 .
.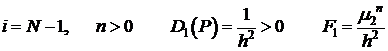 ,
, .
. имеем:
имеем: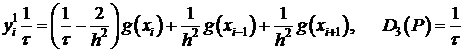 .
.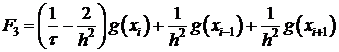 .
.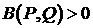 , т.к. окрестность точки Р – пустое множество, т.е. точка Р – единственная.
, т.к. окрестность точки Р – пустое множество, т.е. точка Р – единственная.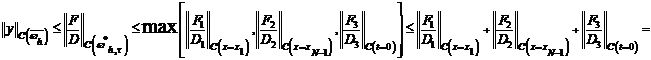
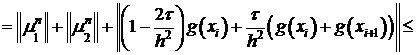


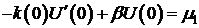
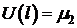 .
.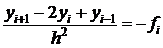 ,
,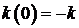 ,
,  .
.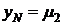
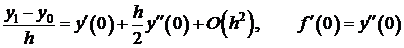 .
.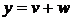 .
.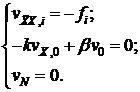

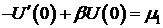
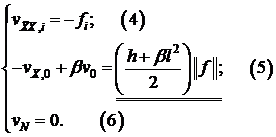
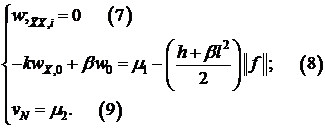
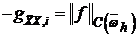 ,
, , продифференцируем.
, продифференцируем.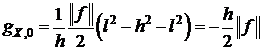 .
. .
.
 .
. .
. в котором
в котором  и
и 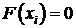 .
. , используя равенство (8).
, используя равенство (8). ;
; ;
;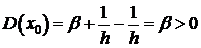 .
. .
.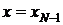 .
.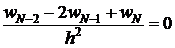 ;
;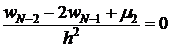 ;
; ;
;
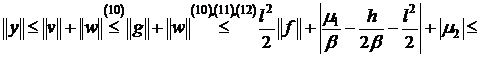 используем неравенство треугольников
используем неравенство треугольников 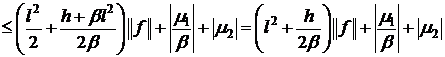 .
. .
. называется сопряженным к
называется сопряженным к 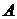 , если
, если 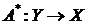 и для любых
и для любых 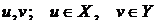 выполняется:
выполняется: 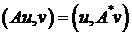 .
. необходимо и достаточно, чтобы в пространстве
необходимо и достаточно, чтобы в пространстве  существовал ортонормированный базис, построенный из собственных векторов оператора
существовал ортонормированный базис, построенный из собственных векторов оператора  ,
,  - числа.
- числа. , что:
, что:  .
.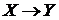 . Для того, чтобы линейный оператор
. Для того, чтобы линейный оператор  существовал и был ограниченным, необходимо и достаточно, чтобы для элемента
существовал и был ограниченным, необходимо и достаточно, чтобы для элемента 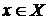 существовала такая константа
существовала такая константа  , не зависящая от
, не зависящая от  , для которой выполнялось неравенство:
, для которой выполнялось неравенство:  . При этом справедлива оценка:
. При этом справедлива оценка: 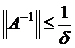 .
. , положительным, если
, положительным, если  .
. существует такая константа
существует такая константа  , не зависящая от
, не зависящая от 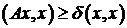 .
.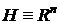 конечномерное пространство, то определения 2 и 3 эквивалентны.
конечномерное пространство, то определения 2 и 3 эквивалентны. , т.е.
, т.е. 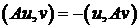 .
. .
.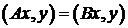 , то
, то  и энергию оператора
и энергию оператора  , можно ввести как отношение неравенств на пространстве линейных операторов.
, можно ввести как отношение неравенств на пространстве линейных операторов.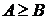 , если
, если  ,
,


