Однородное уравнение  с неоднородными граничными условиями
с неоднородными граничными условиями  ,
, 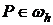 ,
, 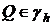 , где
, где  - заданная функция из исходного семейства обладает свойством:
- заданная функция из исходного семейства обладает свойством:  ,
,
т.е. максимальное по модулю значение функции  являющейся решением задачи (2), (3) достигается на границе
являющейся решением задачи (2), (3) достигается на границе  сетки
сетки  .
.
Доказательство.
Результат прямо следует из теоремы 1, т.к. для задачи (2), (3) справедливы одновременно случай 1) и 2) теоремы 1.
1) 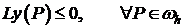 , следовательно наибольшее положительное значение достигается на границе сетки
, следовательно наибольшее положительное значение достигается на границе сетки  .
.
2)  , следовательно наименьшее отрицательное значение достигается на границе сетки
, следовательно наименьшее отрицательное значение достигается на границе сетки  .
.
Также для следствия 1 можно сформулировать его аналог для 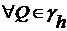 .
.
Следствие 1′.
Пусть дано однородное уравнение из исходного семейства вида:
(4) 
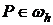 , с граничным условием Дирихле:
, с граничным условием Дирихле:
(5)  ,
,  .
.
Тогда решение задачи (4), (5) не положительно на 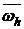 , т.е.
, т.е. 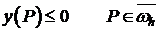 .
.
Теорема сравнения. Мажоранта
Теорема 2.
Пусть поставлена задача (I) с уравнением из исходного семейства вида:
(1) 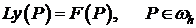 ;
;
(2)  .
.
А также поставлена задача (II):
(3) 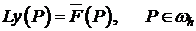 ;
;
(4) 
и выполняются неравенства:
(5′)  ,
, 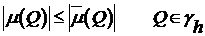
то
( 5) 

Замечание.
Введем обозначение:  ,
,  .
.
Т.о. неравенство (5) можно переписать в виде:  .
.
Задачу (3), (4) называют мажорирующей по отношению к задаче (1), (2).
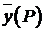 - мажоранта по отношению к
- мажоранта по отношению к  .
.
Доказательство.
Зададим сеточные функции:
(6)  ;
;
(7) 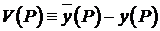 .
.
Нетрудно видеть, что
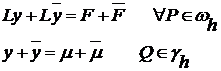
В силу линейности оператора 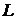 , получаем:
, получаем:
(8) 
(9) 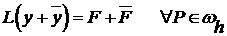 .
.
Задача с учетом (8), (9) может быть записана в виде:
(10)  ;
;
(11)  .
.
Задача (10), (11) удовлетворяет следствию теоремы 1:
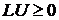 в силу (5′), и граничное условие
в силу (5′), и граничное условие  .
.
Следовательно, 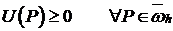 .
.
Аналогично функция  .
.
Вычитая (1) из (3), (2) из (4), и пользуясь линейностью оператора, получаем:

(12) 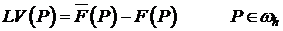 ;
;
(13)  .
.
Таким образом, получаем аналогичную задачу для функции 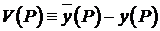 .
.
Итак
(14)  , с другой стороны
, с другой стороны
(15) 
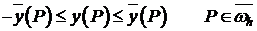
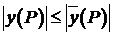 , что и требовалось доказать.
, что и требовалось доказать.
Следствие из теоремы сравнения
Следствие 1. Оценка решения однородной задачи.
Пусть поставлена задача из исходного семейства:
(1)  ;
;
(2) 
Тогда для нормы решения этой задачи справедлива оценка:
(3)  ,
,
также справедлива оценка:

Доказательство.
Для задачи (1), (2) построим мажорирующую задачу вида:
(3.1)  ;
;
(4)  ;
;
правые части (3.1) и (1) удовлетворяют неравенству:
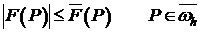
 , по теореме сравнения
, по теореме сравнения  .
.
Если удастся доказать, что  , то требуемый результат будет доказан.
, то требуемый результат будет доказан.
Воспользуемся следствием 4 из теоремы 1, в соответствии с которым для задачи (3.1), (4) справедлива оценка:
 и следовательно,
и следовательно, 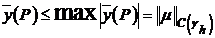 .
.
Доказательство проведено в условиях применимости теоремы 1, т.е.  . Рассмотрим в данном следствии второй случай, когда
. Рассмотрим в данном следствии второй случай, когда  .
.
В силу равенства (4) и из последнего равенства получаем, что 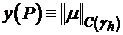 , что и требовалось доказать.
, что и требовалось доказать.
Более того, можно доказать,что если поставлена задача (3.1), (4), взяв обобщение (4)
 и
и  , будет следовать, что
, будет следовать, что  .
.
Доказанное следствие будет далее использовано для оценки решения неоднородного уравнения с оператором вида:
(5) 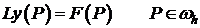 ,
,
(6) 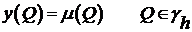 .
.
Решение задачи (5), (6) может быть получено в виде двух функций:
 ,
,
где  - решение задачи:
- решение задачи:
(7)  ;
;
(8) 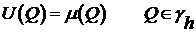 ,
,
 - решение задачи:
- решение задачи:
(9)  ;
;
(10) 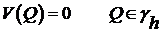 .
.
Поскольку оценка для задачи (7), (8) была получена в следствии 1, то перейдем к оценки решения задачи (9), (10).
Оценка решения неоднородного уравнения



 с неоднородными граничными условиями
с неоднородными граничными условиями  ,
, 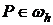 ,
, 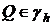 , где
, где  - заданная функция из исходного семейства обладает свойством:
- заданная функция из исходного семейства обладает свойством:  ,
, являющейся решением задачи (2), (3) достигается на границе
являющейся решением задачи (2), (3) достигается на границе  сетки
сетки  .
.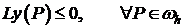 , следовательно наибольшее положительное значение достигается на границе сетки
, следовательно наибольшее положительное значение достигается на границе сетки  , следовательно наименьшее отрицательное значение достигается на границе сетки
, следовательно наименьшее отрицательное значение достигается на границе сетки 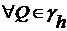 .
. ,
,  .
.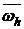 , т.е.
, т.е. 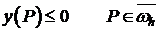 .
.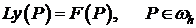 ;
;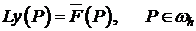 ;
;
 ,
, 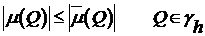


 ,
,  .
. .
.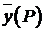 - мажоранта по отношению к
- мажоранта по отношению к  ;
;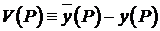 .
.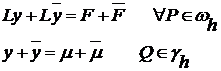
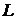 , получаем:
, получаем:
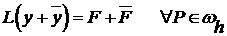 .
. ;
; .
.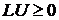 в силу (5′), и граничное условие
в силу (5′), и граничное условие  .
.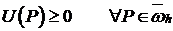 .
. .
.
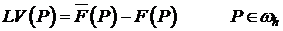 ;
; .
. , с другой стороны
, с другой стороны
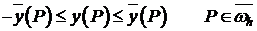
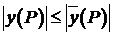 , что и требовалось доказать.
, что и требовалось доказать. ;
; ,
,
 ;
; ;
;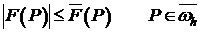
 , по теореме сравнения
, по теореме сравнения  , то требуемый результат будет доказан.
, то требуемый результат будет доказан. и следовательно,
и следовательно, 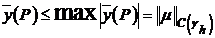 .
. . Рассмотрим в данном следствии второй случай, когда
. Рассмотрим в данном следствии второй случай, когда  .
.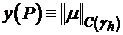 , что и требовалось доказать.
, что и требовалось доказать. и
и  , будет следовать, что
, будет следовать, что  .
.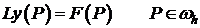 ,
,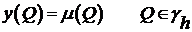 .
. ,
, - решение задачи:
- решение задачи: ;
;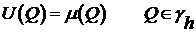 ,
, - решение задачи:
- решение задачи: ;
;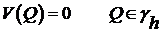 .
.


