Разностная схема, аппроксимирующая задачу Дирихле для уравнения Пуассона в прямоугольнике:
(1)  ;
;
(2) 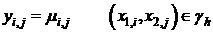 .
.
В предыдущем параграфе была записана в канонической форме:
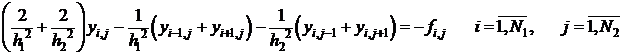 Напомним, что сеточные уравнения имеют следующий канонический вид:
Напомним, что сеточные уравнения имеют следующий канонический вид:
(3)  ;
;
(4)  ..
..
Сравнивая с (3), получаем:
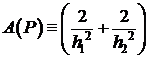 ,
,
 ,
,  .
.
Очевидно, что 
(6)  .
.
Разностное условие (4) можно трактовать, как частный случай записи (3) в которой 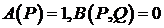 , если
, если 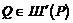 , в этом случае
, в этом случае  .
.
Возможна и другая трактовка граничного условия (4).
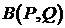 - произвольные положительные числа,
- произвольные положительные числа,
 ,
,  .
.
Кроме того, сеточное уравнение (3) в канонической форме может быть записано в виде:
(3′)  .
.
Формально граничные узлы сетки можно определить двумя способами (в случае условия Дирихле):
1. те узлы сетки, значения в которых  задано, образуют множество
задано, образуют множество 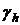 .
.

2.  .
.
Принцип максимума
Напомним определение связности сетки.
Опр.
Сетка  называется связной, если
называется связной, если 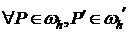 найдется множество узлов:
найдется множество узлов: 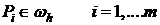 , что выполняется:
, что выполняется:
(7) 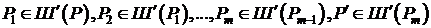 .
.
Некоторые из этих точек, попадающих в окрестность, могут быть и граничными.
Теорема 1. Принцип максимума.
Пусть для сеточной функции  не являющейся тождественной константой для любых
не являющейся тождественной константой для любых 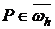 выполняется:
выполняется:
1. 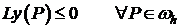 , (считаем, что
, (считаем, что 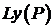 сеточный оператор с коэффициентами, удовлетворяющими условию (5), а сетка
сеточный оператор с коэффициентами, удовлетворяющими условию (5), а сетка 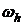 -связная), тогда сеточная функция
-связная), тогда сеточная функция  не может достигать наибольшего положительного значения во внутренних узлах сетки.
не может достигать наибольшего положительного значения во внутренних узлах сетки.
2.  , тогда сеточная функция
, тогда сеточная функция  не может достигать наименьшего отрицательного значения во внутренних узлах сетки.
не может достигать наименьшего отрицательного значения во внутренних узлах сетки.
Доказательство.
Предположим противное: существует такая точка  . Тогда найдется хотя бы одна точка
. Тогда найдется хотя бы одна точка  .
.
Так как  , среди всех
, среди всех  зафиксируем
зафиксируем 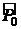 .
.
В силу связанности сетки существует конечное множество узлов:
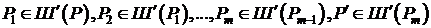 .
.
Рассмотрим уравнение (3′) в точке 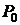 .
.
(8)  .
.
В силу (5, 6):  в силу (5):
в силу (5):  .
.
Если использовать «сильное» определение, то точка 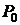 - точка в которой сеточная функция достигает наибольшего значения, то
- точка в которой сеточная функция достигает наибольшего значения, то 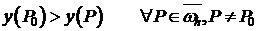 , то неравенство (8) не выполняется, т.к.
, то неравенство (8) не выполняется, т.к. 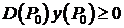 , а
, а  .
.
Более интересным является применение другого «слабого» определения наибольшего значения: 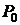 - точка в которой сеточная функция достигает своего наибольшего значения, то
- точка в которой сеточная функция достигает своего наибольшего значения, то  при условии, что найдется хотя бы одна точка
при условии, что найдется хотя бы одна точка  .
.
Будем ориентироваться на это более содержательное определение.
Тогда 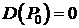 ,
,  , следовательно
, следовательно 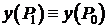 . Выберем точку
. Выберем точку 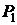 в качестве центра шаблона.
в качестве центра шаблона.
Имеем:  .
.
Так как 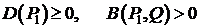 , то
, то  . Следовательно,
. Следовательно, 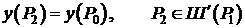 .
.
Аналогично проделав для остальных узлов неравенства (3′) тоже самое, приходим к цепочке равенств:  .
.
Теперь рассмотрим левую часть неравенства (8).
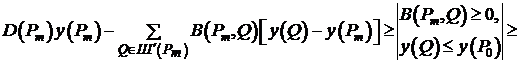
 .
.
Полученное неравенство противоречит предположению 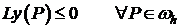 .
.
Следствия из принципа максимума
Следствие 1.
Пусть выполнены условия предыдущей теоремы, кроме одного  может быть тождественной константой на сетке.
может быть тождественной константой на сетке.
Сеточная функция  , заданная
, заданная  неотрицательна на границе
неотрицательна на границе  , т.е.
, т.е. 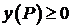 и имеет место
и имеет место 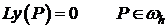 .
.
Тогда функция 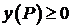
 .
.
Доказательство.
1. Пусть 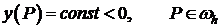 ;
;
2. 
Рассмотрим первый пункт.
Выберем в качестве точки 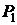 так называемый приграничный узел, т.е.
так называемый приграничный узел, т.е. 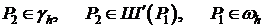 .
.
Рассмотрим уравнение (3′) в точке 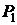 .
.
(9) 
1) 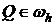 , тогда
, тогда  , т.к.
, т.к. 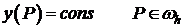 .
.
2) 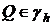 , тогда
, тогда  ,
, 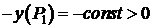
 ,
,  .
.
Отсюда вытекает, что левая часть (9) отрицательна, что противоречит условию, что  .
.
Рассмотрим второй пункт.
Пусть существует точка  , тогда в силу предыдущей теоремы 1
, тогда в силу предыдущей теоремы 1  , следует, что нет такой точки
, следует, что нет такой точки  .
.
Если точка 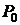 не единственная точка сетки, в которой значение функции отрицательно, то среди всех этих точек
не единственная точка сетки, в которой значение функции отрицательно, то среди всех этих точек  следует выбрать такую точку, что
следует выбрать такую точку, что 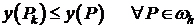 , которая удовлетворяет неравенству. Если
, которая удовлетворяет неравенству. Если 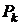 не одна, то выбирается любая.
не одна, то выбирается любая.
Следствие 2.
Однородное уравнение  с однородными граничными условиями
с однородными граничными условиями  ,
, 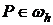 ,
, 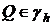 имеет только тривиальное решение.
имеет только тривиальное решение.
Доказательство.
Из теоремы
1) 
 , если
, если 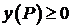 ;
;
2) 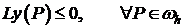
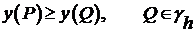 , если
, если 
Из 1) и 2) следует, что  и
и 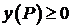 , следовательно
, следовательно  .
.
Следствие 3.
Исходное сеточное уравнение  при условии, что выполняются ограничения (5), (6), а также сетка связная, имеет единственное решение.
при условии, что выполняются ограничения (5), (6), а также сетка связная, имеет единственное решение.
Это следствие вытекает из известной теоремы алгебры, т.к. соответствующая однородная система 
 имеет тривиальное решение в силу следствия 2, следовательно неоднородная система имеет единственное решение.
имеет тривиальное решение в силу следствия 2, следовательно неоднородная система имеет единственное решение.
Опр.
Сеточное уравнение вида:
(1) 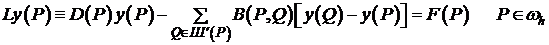
будем называть уравнением, а оператор L – оператором из исходного семейства, если (1) определено во внутренних узлах сетки 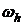 , а
, а 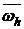 - связное множество относительно шаблона.
- связное множество относительно шаблона.




 ;
;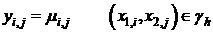 .
.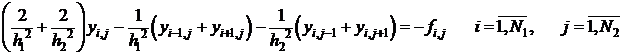 Напомним, что сеточные уравнения имеют следующий канонический вид:
Напомним, что сеточные уравнения имеют следующий канонический вид: ;
; ..
..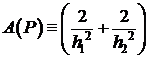 ,
, ,
,  .
.
 .
.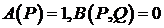 , если
, если 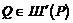 , в этом случае
, в этом случае  .
.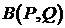 - произвольные положительные числа,
- произвольные положительные числа, ,
,  .
. .
. задано, образуют множество
задано, образуют множество 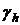 .
.
 .
. называется связной, если
называется связной, если 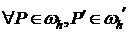 найдется множество узлов:
найдется множество узлов: 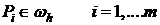 , что выполняется:
, что выполняется: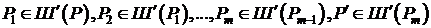 .
.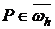 выполняется:
выполняется: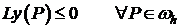 , (считаем, что
, (считаем, что 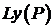 сеточный оператор с коэффициентами, удовлетворяющими условию (5), а сетка
сеточный оператор с коэффициентами, удовлетворяющими условию (5), а сетка 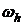 -связная), тогда сеточная функция
-связная), тогда сеточная функция  , тогда сеточная функция
, тогда сеточная функция  . Тогда найдется хотя бы одна точка
. Тогда найдется хотя бы одна точка  .
. , среди всех
, среди всех  зафиксируем
зафиксируем 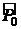 .
.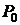 .
. .
. в силу (5):
в силу (5):  .
.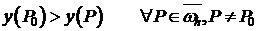 , то неравенство (8) не выполняется, т.к.
, то неравенство (8) не выполняется, т.к. 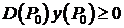 , а
, а  .
. при условии, что найдется хотя бы одна точка
при условии, что найдется хотя бы одна точка 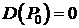 ,
,  , следовательно
, следовательно 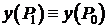 . Выберем точку
. Выберем точку 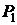 в качестве центра шаблона.
в качестве центра шаблона. .
.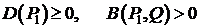 , то
, то  . Следовательно,
. Следовательно, 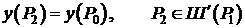 .
. .
.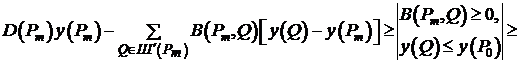
 .
. неотрицательна на границе
неотрицательна на границе  , т.е.
, т.е. 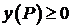 и имеет место
и имеет место 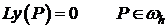 .
.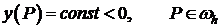 ;
;
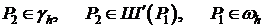 .
.
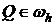 , тогда
, тогда  , т.к.
, т.к. 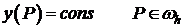 .
.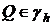 , тогда
, тогда  ,
, 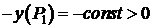
 ,
,  .
. .
. , тогда в силу предыдущей теоремы 1
, тогда в силу предыдущей теоремы 1  следует выбрать такую точку, что
следует выбрать такую точку, что 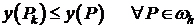 , которая удовлетворяет неравенству. Если
, которая удовлетворяет неравенству. Если 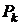 не одна, то выбирается любая.
не одна, то выбирается любая. с однородными граничными условиями
с однородными граничными условиями  ,
, 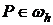 ,
, 
 , если
, если 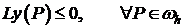
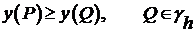 , если
, если 
 при условии, что выполняются ограничения (5), (6), а также сетка связная, имеет единственное решение.
при условии, что выполняются ограничения (5), (6), а также сетка связная, имеет единственное решение.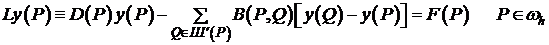
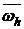 - связное множество относительно шаблона.
- связное множество относительно шаблона.



